Методические указания к решению расчетно-графической работы №2

Решение задач на равновесие твердого тела, независимо от взаимного расположения приложенных к телу сил, рекомендуется проводить в следующем порядке:

1. выделить твердое тело, равновесие которого надо рассмотреть для отыскания неизвестных величин;
2. изобразить активные силы;
3. если твердое тело несвободно, то, применив закон освобождаемости от связей, приложить к нему соответствующие реакции связей;
4. рассмотреть равновесие данного несвободного твердого тела, как тела свободного, находящегося под действием активных сил и реакций связи;
5. убедиться в том, что данная задача является статически определимой, т.е. число неизвестных величин не более трех;
6. выбрать направление осей декартовых координат и точку (или точки) относительно которой предполагается составить уравнение моментов. Оси координат целесообразно направить так, чтобы некоторые неизвестные силы оказались перпендикулярными к этим осям. Тогда величины этих неизвестных сил в соответствующее уравнение проекций не войдут.

Точку, относительно которой должно быть составлено уравнение моментов, следует выбрать в точке пересечения линий действия двух неизвестных сил. Это дает возможность непосредственно определить из соответствующего уравнения моментов величину третьей неизвестной силы. Однако, если эта точка расположена так, что вычисление плеч при определении моментов сил представляет значительные трудности, то лучше уравнение моментов составить относительно другой точки, в которое войдут величины двух неизвестных сил, и затем совместно решить полученную систему уравнений;

7. составить уравнение равновесия твердого тела. При решении задачи используется любое из трех видов уравнений равновесия:

	Если произвольная плоская система сил уравновешена, то алгебраическая сумма проекций всех сил на оси X и Y равна нулю, а также равна нулю алгебраическая сумма моментов всех сил относительно любой точки, лежащей на плоскости.
	Если произвольная плоская система сил уравновешена, то алгебраические суммы моментов сил относительно двух любых точек, а также алгебраическая сумма проекций сил на ось, не перпендикулярную прямой проходящей через эти точки, равны нулю.
	Если произвольная плоская система сил уравновешена, то алгебраические суммы моментов сил относительно любых трех точек, не лежащих на одной прямой, равны нулю.

1. решить систему полученных уравнений равновесия и определить неизвестные величины. Если в результате решения знак величины какой-либо силы или момента окажется отрицательным, то это означает, что направление силы или момента противоположно тому, которое было предварительно выбрано;
2. сделать проверку и убедиться, что неизвестные величины найдены верно.

 

 

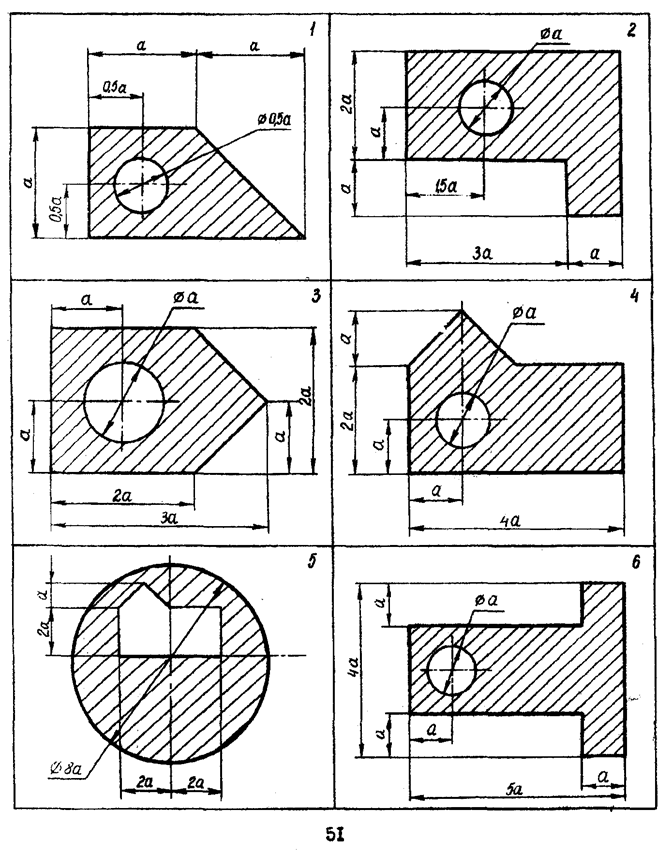
Расчетно-графическая работа №3 «ЦЕНТР ТЯЖЕСТИ»

Задание 1. Рассчитать координаты центра тяжести заштрихованной части изображенной плоской фигуры относительно выбранной системы координат.

 

 

 

Таблица 3. Исходные данные к РГР №3

 

 

№ варианта	№ схемы	а,см.	№ варианта	№ схемы	а,см.

 

Задание 2. Определить координаты центра тяжести сечения, изображенного на
рисунке.

Методические указания к решению расчетно-графической работы №3

Решение задач на определение центра тяжести плоской фигуры рекомендуется проводить в следующем порядке:

1. сложное сечение разбиваем на простые, положение центра тяжести которых известно, либо легко может быть определено;

2. выбираем произвольно координатные оси. Если плоская фигура имеет ось симметрии, то рекомендуется провести одну из координатных осей вдоль оси симметрии. Так как центр тяжести С сечения лежит на оси симметрии (т.е. на одной из координатных осей), то необходимо определить лишь одну координату;

3. определяем площади простых сечений;

4. определяем координаты центров тяжести простых сечений относительно выбранных осей координат. Координаты центров тяжести простейших фигур смотреть в конце данного раздела;

5. найденные значения подставляем в формулы:

 

 

где А₁, А₂ ... А_К - площади простых сечений,

x_1, x₂ … x_K,

y_1, y₂ … y_К – координаты центра тяжести простых сечений;

 

6. значения X_C,Y_C откладываем от выбранных осей координат с учетом знака, т.е. от точки О в положительном направлении координаты со знаком «плюс» и в отрицательном направлении координаты со знаком «минус».