
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автокорреляция: причины, последствия.Содержание книги Поиск на нашем сайте
Предпосылки: отсутствие тесной взаимосвязи. H0: нету автокорреляции. Cov( Автокорреляция или или последовательная корреляция определяется как корреляция между наблюдаемыми показателями, упорядоченными по времени. (Чаще при временных рядах) Постоянная направленность воздействия не включаемых в уравнение переменных является наиболее частой причиной положительной автокорреляции.
Cov(
Отрицательная автокорреляция означает, что за положительным отклонением следует отрицательное и наоборот. Основные причины, вызывающие появление автокорреляции: 1. Ошибки стратификации (в модели не учтена важная объясняющая переменная или выбрана не верная форма зависимости). 2. Инерция (связана с цикличностью экономических показателей). 3. Эффект паутины. 4. Сглаживание данных (использование усреднённых показателей). Последствия автокорреляции: 1. Оценки остаются линейными и несмещёнными, но перестают быть эффективными. 2. Дисперсии оценок являются смещёнными, часто заниженными => t-статистика завышена. 3. Оценка дисперсии ошибок является смещённой и часто заниженной. 4. Неверные выводы по t- и f-статистикам.
Методы обнаружения автокорреляции Рассмотрим возможные методы определения автокорреляции. 1. Графический метод Существует несколько вариантов графического определения автокорреляции. Один из них, увязывающий отклонения et с моментами t их получения (их порядковыми номерами i), приведен на рис. Это так называемые последовательно-временные графики. В этом случае по оси абсцисс обычно откладываются либо момент получения статистических данных, либо порядковый номер наблюдения, а по оси ординат отклонения εt (либо оценки отклонений et). Естественно предположить, что на рис. а — г имеются определенные связи между отклонениями, т.е. автокорреляция имеет место. Отсутствие зависимости на рисунке д, скорее всего, свидетельствует об отсутствии автокорреляции.
Метод рядов Последовательно определяются знаки отклонений еt. Например, (-----)(+++++++)(---)(++++)(-), т. е. 5 “-“, 7 "+", 3 “-“, 4 "+", 1 "-" при 20 наблюдениях. Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называется длиной ряда. Визуальное распределение знаков свидетельствует о неслучайном характере связей между отклонениями. Если рядов слишком мало по сравнению с количеством наблюдений n, то вполне вероятна положительная автокорреляция. Если же рядов слишком много, то вероятна отрицательная автокорреляция. Для более детального анализа предлагается следующая процедура. Пусть n - объем выборки; n1 - общее количество знаков при n наблюдениях (количество положительных отклонений et); n2 - общее количество знаков "—" при n наблюдениях (количество отрицательных отклонений et); к - количество рядов. При достаточно большом количестве наблюдений (n1 > 10, n2 > 10) и отсутствии автокорреляции случайная величина k имеет асимптотически нормальное распределение с
Тогда, если M(k) - uα\2*D(k) < k < M(k) + uα/2*D(k), то гипотеза об отсутствии автокорреляции не отклоняется. Тест Дарбина-Уотсона Предполагаем, что случайная последовательность
H0: H1:
На практике вместо коэффициента корреляции используется статистика Дарбина-Уотсона:
Очевидно, что эта статистика связана с коэффициентом корреляции R:
Критическое значение DW зависит от n, k и Выводы по тесту Д-У: На практике применение критерия Дарбина — Уотсона основано на сравнении величины 1. Если 2. Если 3. Если Когда расчетное значение Также с помощью данного критерия выявляют наличие коинтеграции между двумя временными рядами. В этом случае проверяют гипотезу о том, что фактическое значение критерия равно нулю. С помощью метода Монте-Карло были получены критические значения для заданных уровней значимости. В случае, если фактическое значение критерия Дарбина — Уотсона превышает критическое, то нулевую гипотезу об отсутствии коинтеграции отвергают. Ограничения при использовании: 1) только для тех моделей, которые содержат свободный член; 2) случайные отклонения определяются авторегрессионной схемой первого порядка; 3) статистические данные должны иметь одинаковую периодичность; 4) не применяется для моделей, содержащих в составе объясняющих переменных зависимую переменную с временным лагом 1.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 814; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.110.45 (0.012 с.) |

 t
t  ; частный случай: Cov(
; частный случай: Cov( .
.
 .
.

 образует авторегрессионный процесс 1-го порядка, т.е. удовлетворяет рекуррентному соотношению:
образует авторегрессионный процесс 1-го порядка, т.е. удовлетворяет рекуррентному соотношению:  (2-го порядка:
(2-го порядка:  ), где
), где  -последовательность независимых нормально распределенных случайных величин с
-последовательность независимых нормально распределенных случайных величин с 
 - некоторый параметр, называемый коэффициентом авторегрессии;
- некоторый параметр, называемый коэффициентом авторегрессии; 
 - положительная автокорреляция; иначе – отрицательная.
- положительная автокорреляция; иначе – отрицательная.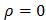

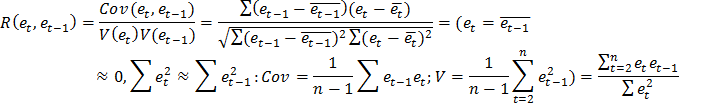


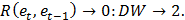

 (уровень значимости) и всей матрицы X.
(уровень значимости) и всей матрицы X. с теоретическими значениями
с теоретическими значениями  и
и  для заданных числа наблюдений
для заданных числа наблюдений  , числа независимых переменных модели
, числа независимых переменных модели  и уровня значимости
и уровня значимости  .
.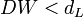 , то гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция);
, то гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция); , то гипотеза не отвергается;
, то гипотеза не отвергается; , то нет достаточных оснований для принятия решений.
, то нет достаточных оснований для принятия решений.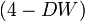 .
.



