
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторная авторегрессия (VAR)Содержание книги Поиск на нашем сайте
VAR – модель, в которой несколько зависимых переменных зависят от собственных лагов и лагов других переменных. Используется при эконометрическом моделировании и прогнозировании как в макро-, так и микроэкономике. VAR(p) – векторная авторегрессия порядка p – определяется векторным уравнением порядка p следующего вида:
Ковариационная матрица одновременных ошибок диагональна. Приведем покомпонентную запись в виде системы авторегрессионных уравнений:
Рассмотрим пример двумерного вектора и 1 лага.
VAR(1):
Или:
VAR(p):
Обозначим:
Представим VAR(1) в виде бесконечного скользящего среднего: Чтобы ряд сходился, необходимо, чтобы его члены затухали; чтобы в пределе при Чтобы временной ряд VAR(p) был стационарным (т.е. мат.ожидание не зависело от времени)
Модели бинарного выбора. Пусть имеем n переменных,наличие/отсутствие признака yi = E(εi | xi)=i E(yi | xi)= xi`β. Условное мат.ожид. приxi: E(yi | xi)=P(yi=1| xi). xβ= P(yi=1| xi), 0<= xi`β<=1. При yi=1 εi=1- xi`β, при yi=0 εi=- xi`β. Т.о. при фиксир. xi отклонение случ.ошибки принимают только 2 значения, вер-сти кот.: P{ εi=1- xi`β| xi }=P{ yi=1| xi }= xi`β P{ εi=- xi`β| xi }=P{ yi=0| xi }=1- xi`β. Соотв-но случ.величина при фиксир. xi и меет мат.ожид.: E(εi | xi)=(1- xiβ)* P(εi=1- xi`β| xi)+(-xi`β P(εi=- xi`β| xi)=0. Дисперсия D{ εi | xi }=E{ εi 2(xi)}- (E(εi | xi))2=(1- xi`β)2 xi`β+(- xi`β)(-xi`β)=-xi`β(1- xi`β). Модель бинарного выбора yi=Ф(α+ βxi)+ εi. Оценки параметров В общем случае исп-ся n переменных: yi=G(β1xi1+…+ βpxip)+ εi. Обычно в качестве ф-ции G(z) исп-ся след.ф-ции: Пробит-модель Ф(z)=1/Ö2п Логит-модель l(z)=ez/1+ez – станд. логистич.распределение. Гомпит-модель G(z)=-exp(-ez) – ф-ция станд.рспределения экстрем. значений 1-го типа. Показатели качества модели бинарного выбора: R2=RSS/TSS=1-ESS/TSS - коэф.детерминации. Рассмотрим «тривиальную модель»,кот. в качестве объясн-щей переменной вкл. единственную переменную=1,т.е.своб.член yi= βi+εi. , xi1=1
Одна из возможных характеристик, определ-щих качество подобранной модели-сравнение кол-в неправ.предсказаний, получ-но выбран.модели и по модели, в кот. в кач-ве объясн-щей переменной выступает константа(«тривиальные модели»). Если yi=1,то G(xi` Прогнозное значение Количество неправильных предсказаний по выбранной модели: nw,1=S| yi - Доля неправ.предсказаний ϑw,1=(1/n)S| yi - При этом ϑw,0= В качестве показателя качества модели можно взять R2predict=1- ϑw,1/ ϑw,0=1-S(yi - Пусть L1-max ф-ции правдоподобия для выбран.модели, L0- для тривиальной модели. При этом L0<= L1<=1. lnL0<=lnL1<=0. Pseudo R2=1-((1/1+2(lnL1- lnL0)/n). McFaddenR2=1-(lnL1/(lnL0)
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.210 (0.007 с.) |

 где t – дискретное время.
где t – дискретное время. N-наблюдений за состоянием экономической системы в момент времени t.
N-наблюдений за состоянием экономической системы в момент времени t. - значение i-й наблюдаемой эндогенной переменной в момент времени t.
- значение i-й наблюдаемой эндогенной переменной в момент времени t. – вектор-столбец констант.
– вектор-столбец констант. - матрица коэффициентов авторегрессии, s=1,…,p, соответствующую величине лага s.
- матрица коэффициентов авторегрессии, s=1,…,p, соответствующую величине лага s. - векторный белый шум со следующими свойствами:
- векторный белый шум со следующими свойствами: ,
, 
 i –номер уравнения, t –номер наблюдения, i=1,..,N. – линейная комбинация констант и p первых лагов всех N переменных.
i –номер уравнения, t –номер наблюдения, i=1,..,N. – линейная комбинация констант и p первых лагов всех N переменных. - темп роста денежной массы.
- темп роста денежной массы. – дефлятор ВВП.
– дефлятор ВВП.


 =
= 

 =
= 
 ,
,  ,
, 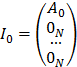 ,
, 

 …
… .
. последовательность матриц
последовательность матриц  , а для этого надо, чтобы собственные значения матриц А лежали внутри единичного корня:
, а для этого надо, чтобы собственные значения матриц А лежали внутри единичного корня:  .
. , а его ковариационная матрица не зависела от сдвига начала отсчета времени:
, а его ковариационная матрица не зависела от сдвига начала отсчета времени:  . Достаточно, чтобы все собственные значения
. Достаточно, чтобы все собственные значения  матрицы А являлись корнями уравнения
матрицы А являлись корнями уравнения 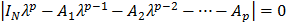 лежали внутри единичного круга.
лежали внутри единичного круга.


 . yi= β1xi1+…+ βpxip+ εi,где xi1,…, xip – объясняющие переменные, β1.. βp- неизв.параметры,кот.подлежат оценке, εi- случ.ошибки, отраж. влияние неизв.факторов.
. yi= β1xi1+…+ βpxip+ εi,где xi1,…, xip – объясняющие переменные, β1.. βp- неизв.параметры,кот.подлежат оценке, εi- случ.ошибки, отраж. влияние неизв.факторов. =
= 
 =1/
=1/ 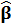 . Если применить МНК: F(α, β)=S(yi-Ф(*))=>min, но Ф нелин.по параметрам. При применении МНК к нел. ф-ции сталкиваемся с проблемой гетероскед-сти. Можно использовать взвешенную МНК: веса wi=1/D(εi | xi).Поэтому для оценивания неизв.параметров ф-ции Ф исп-ся метод максим. правдоподобия(ММП).
. Если применить МНК: F(α, β)=S(yi-Ф(*))=>min, но Ф нелин.по параметрам. При применении МНК к нел. ф-ции сталкиваемся с проблемой гетероскед-сти. Можно использовать взвешенную МНК: веса wi=1/D(εi | xi).Поэтому для оценивания неизв.параметров ф-ции Ф исп-ся метод максим. правдоподобия(ММП). dt – ф-ция чтанд.норм.распределния N(0;1)
dt – ф-ция чтанд.норм.распределния N(0;1) -ср.значение.
-ср.значение.  =
= 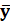 => ESS=TSS R2=0.Если в правой части добавляется новая объясняющая переменная => R2 возрастаеи, а max, если вып-ся соотношение yi= xi`β.
=> ESS=TSS R2=0.Если в правой части добавляется новая объясняющая переменная => R2 возрастаеи, а max, если вып-ся соотношение yi= xi`β.
 >1/2 или
>1/2 или 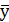 >1/2. Т.е. значения yi=1 наблюдается более, чем в половине наблюдений, а yi=0 не более чем ½ наблюдений.
>1/2. Т.е. значения yi=1 наблюдается более, чем в половине наблюдений, а yi=0 не более чем ½ наблюдений. .
. LRI-индекс отношения правдоподобия.
LRI-индекс отношения правдоподобия.


