
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел I. Начертательная геометрияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Конспект лекций по дисциплине «Начертательная геометрия» для студентов направления 151900.62 «Конструкторско-технологическое обеспечение машиностроительных производств», всех форм обучения
Сарапул Кафедра «Технология машиностроения, металлорежущие станки и инструменты» Составитель ст. преп. Мосалев Н.А.
Составлено на основании федерального государственного образовательного стандарта высшего профессионального образования
Рекомендовано на заседании кафедры «Технология машиностроения, металлорежущие станки и инструменты». Протокол №10 от 01 сентября 2014г.
Начертательная геометрия: Конспект лекций по дисциплине «Начертательная геометрия»/ Составитель Мосалев Н.А. - Сарапул, 2014 – 74с.
Введение Развитие инженерно-технических производств требует формирования и развития качественных профессиональных компетенций у современных инженерных кадров таких, например, как пространственно-графических компетенций, образно-графических представлений, развития изобретательских и творческих способностей будущих инженеров. Одним из инструментов формирования таких компетенций у студентов инженерных направленностей является такой предмет, как начертательная геометрия. Этот предмет давно является одной из обязательных общепрофессиональных дисциплин в технических вузах мира. Следует отметить, что начертательная геометрия по своему содержанию занимает особое место среди других наук, так как она является лучшим средством развития у человека пространственно-образного воображения. Встречается глубокое ошибочное мнение, что при внедрении в учебный процесс дисциплины «Компьютерная графика» не нужна будет дисциплина «Начертательная геометрия». Эффективность использования машин однозначно зависит от знаний основ Начертательной геометрии и умения использовать их как в стадии разработки системных программ, так и в решении прикладных задач. Человек, не умеющий читать и разрабатывать чертёж на бумаге, не может осмысленно это сделать и при помощи компьютера. Интенсификация учебного процесса в вузах выдвигает новые требования к методике и средствам обучения, к повышению качества подготовки специалистов. 50% учебного времени, при обучении бакалавров, отводится на самостоятельное изучение предметов. В связи с этим краткий конспект лекций по начертательной геометрии должен давать возможность выбора материала, содержать сведения, необходимые не только для учебного процесса, но и для организации научно-исследовательской работы со студентами, для решения инженерных задач, для использования методики проблемного обучения.
Данное пособие представляет информативную часть и содержит сжатую теоретическую информацию, которая необходима при подготовке к экзамену по начертательной геометрии. Кроме того, представленные материалы позволяют студенту более подробно изучить основные разделы начертательной геометрии самостоятельно.
РАЗДЕЛ I. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ ОБОЗНАЧЕНИЯ И СИМВОЛЫ 1. Точки - заглавные буквы латинского алфавита: А, В, С, D …, а также цифры: 1, 2, 3… 2. Линии - строчные буквы латинского алфавита: а, в, с, d… 3. Углы - строчные буквы греческого алфавита: j, w, m … 4. Плоскости - строчные буквы греческого алфавита a,b, g … 5. Плоскости проекций: Н; П1 - горизонтальная; V; П2- фронтальная; W; П3 - профильная. 6. Оси проекций - строчные буквы: х, y, z. 7. Проекции точек: на горизонтальную плоскость проекций - А′, В′, С′ …; на фронтальную плоскость проекций - А ″, В ″, С ″…; на профильную плоскость проекций - А ″′, В ″′, С ″′… 8. Следы плоскости: горизонтальный - a Н, βН …; фронтальный - a V, βV …; профильный - a W, βW … 9. Символы: ║ - параллельность; ^- перпендикулярность; ∩ - пересечение; ÷ - скрещивание;
= - совпадают;
ЗАНЯТИЕ 1. МЕТОДЫ ПРОЕЦИРОВАНИЯ Отображение геометрической фигуры на плоскость можно осуществить путем проецирования ее точек на эту плоскость.
ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Центральное проецирование является наиболее общим случаем получения проекций геометрических фигур. Сущность метода:
точка S, не принадлежащая плоскости α. Возьмем произвольную точку А, не принадлежащую плоскости α (рис. 1.1). Проведем луч SA. SA
Здесь: α - плоскость проекций; S - центр проекций; SA, SВ – проецирующие лучи; А α, В α - центральные проекции точек А и В на плоскость α. Аппарат центрального проецирования: плоскость α, точка S. Утверждение: любой точке соответствует одна и только одна центральная проекция. Обратное утверждение не имеет смысла.
ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ Параллельное проецирование - частный случай центрального проецирования, при котором центр проекций удален в бесконечность. Сущность метода:
Дано: плоскость α, точка S - бесконечно удалена от α. Очевидно, что при таком положении центра проекций проецирующие лучи s будут параллельны друг другу (рис. 1.2). Аппарат параллельного проецирования: плоскость проекций α, направление проецирования s. Основные свойства параллельного проецирования: 1. Проекция точки есть точка. 2. Проекция прямой на плоскость есть прямая. 3. Если в пространстве точка принадлежит линии, то проекция этой точки принадлежит проекции линии. 4. Проекции взаимно параллельных прямых также взаимно параллельны, а отношение отрезков таких прямых равно отношению их параллельных проекций. 5. Точка пересечения проекций пересекающихся прямых является точкой пересечения этих прямых. 6. Плоская фигура, параллельная плоскости проекций, проецируется на эту плоскость в конгруэнтную фигуру. 7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин. 8. Параллельный перенос оригинала или плоскости проекций не изменяет вида и размеров проекции оригинала.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Перечислите основные методы проецирования, их сущность. 2. Как изображают пространственную модель координатных плоскостей? 3. Что называют эпюром? 4. Каким образом пространственную модель координатных плоскостей, состоящую из трех взаимно перпендикулярных плоскостей, преобразуют в эпюр? 5. Как обозначают проекции точки на плоскости проекций Н (П1), V (П2), W (П3)? 6. Какие координаты определяют проекции точки на плоскости Н, V, W? 7. Как построить недостающую проекцию точки по двум данным проекциям? 8. Какие координаты определяют расстояние от точки до плоскостей Н, V, W? 9. Точка А (0,30,0) принадлежит … - только горизонтальной плоскости проекции - оси x - оси y - оси z - только профильной плоскости проекций 10. Точка А (0,0,30) принадлежит … - только горизонтальной плоскости проекции - оси x - оси y - оси z - только профильной плоскости проекций 11. Точка С (0,30,40) принадлежит … - только горизонтальной плоскости проекции - только профильной плоскости проекции - только фронтальной плоскости проекции - оси х - оси y
12. Точка К принадлежит …
- только фронтальной плоскости проекции -только профильной плоскости проекции - оси y - оси z
13. Точка N принадлежит …
- только фронтальной плоскости проекции - только профильной плоскости проекции - оси y - оси z
14. Точка М принадлежит …
- оси z - только горизонтальной плоскости проекции - только фронтальной плоскости проекции - только профильной плоскости проекции
15. Точка М принадлежит …
- только горизонтальной плоскости проекции - только фронтальной плоскости проекции
- только профильной плоскости проекции - оси х - оси z
16. Точка N принадлежит …
- только фронтальной плоскости проекции - только профильной плоскости проекции - оси х - оси z 17. Выше всех расположена точка …
- А - В - С - Д - Е
18. Дальше всех от плоскости V расположена точка…
- А - В - С - Д - Е
ЗАНЯТИЕ 2 3. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПРЯМОЙ
При ортогональном проецировании на плоскость прямая проецируется в прямую. Поэтому, для определения проекции прямой достаточно знать проекции двух точек, принадлежащих этой прямой.
ПРЯМЫЕ ОБЩЕГО ПОЛОЖЕНИЯ Прямая общего положения - это прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций (рис. 3.1, 3.2).
ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ. Прямая частного положения - это прямая параллельная или перпендикулярная одной из плоскостей проекций.
Прямые уровня
Прямая, параллельная горизонтальной плоскости проекций, называется горизонталью h (рис. 3.3). Все точки горизонтали удалены на одинаковое расстояние от плоскости П1.
Прямая, параллельная фронтальной плоскости проекций, называется фронталью f (рис. 3.4 ). Все точки фронталиудалены на одинаковое расстояние от плоскости П2.
Прямая, параллельная профильной плоскости проекций, называется профильной прямой w (рис. 3.5). Все точки профильной прямой удалены на одинаковое расстояние от плоскости П3. Проецирующие прямые Проецирующая прямая - прямая, перпендикулярная какой-либо плоскости проекций и параллельная двум другим.
Прямая, перпендикулярная горизонтальной плоскости проекций и параллельная двум другим называется горизонтально-проецирующей (рис. 3.6). Такая прямая проецируется на плоскость П1 в точку.
Прямая, перпендикулярная фронтальной плоскости проекций и параллельная двум другим называется фронтально-проецирующей (рис. 3.7). Такая прямая проецируется на плоскость П2 в точку.
Прямая, перпендикулярная профильной плоскости проекций и параллельная двум другим называется профильно-проецирующей (рис. 3.8). Такая прямая проецируется на плоскость П3 в точку. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
Если прямые в пространстве параллельны, то на чертеже параллельны их одноименные проекции. На рис. 3.12 – m ║ n.
Если прямые в пространстве пересекаются, то на чертеже пересекаются их одноименные проекции. При этом проекции точек пересечения лежат на одной линии связи.
На рис. 3.13 – m ∩ n = K.
Если прямые в пространстве скрещиваются, то на чертеже их одноименные проекции могут пересекаться, но проекции точек пересечения не лежат на одной линии связи. На рис. 3.14 – m ÷ n.
ТЕОРЕМА О ПРЯМОМ УГЛЕ Для ортогонального проецирования справедлива теорема: для того чтобы прямой угол проецировался без искажений необходимо и достаточно, чтобы одна из его сторон была параллельна плоскости проекций, а вторая – не перпендикулярна к этой плоскости (рис. 3.16).
∟ ABC = 90º, AB ║ П1, BC не перпендикулярна П1, следовательно, ∟ A′B′C′ = 90º.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Как определить положение прямой относительно плоскостей проекций? 2. Как располагается горизонтальная проекция отрезка, если его фронтальная проекция равна самому отрезку? 3. Как называется прямая, если две ее проекции параллельны двум плоскостям проекций? 4. Как определить по проекциям прямых их взаимное положение? 5. Каким способом можно определить натуральную величину отрезка общего положения? 6. На каком чертеже прямая l является горизонтально-проецирующей?
- рис. б) - рис. в)
- рис. а) - рис. б) - рис. в)
8. На каком чертеже прямые c и d является параллельными?
- рис. а) - рис. б) - рис. в)
- рис. а) - рис. б)
10. Прямой а принадлежат точки …
- А и Е - В и D - В и Е - D и Е
ЗАНЯТИЕ 3 СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТЕЙ
На чертеже плоскость может быть задана следующими способами: 1. тремя точками, не принадлежащими одной прямой (рис. 4.1, а); 2. прямой и точкой, не лежащей на ней (рис. 4.1, б); 3. двумя параллельными прямыми (рис. 4.1, в); 4. двумя пересекающими прямыми (рис. 4.1, г); 5. плоской геометрической фигурой (рис. 4.1, д); 6. следами.
На рис. 4.2, а показано наглядное изображение плоскости a. Линию пересечения плоскости с горизонтальной плоскостью проекций называют горизонтальным следом плоскости (a Н), с фронтальной - фронтальным следом плоскости (a V), с профильной - профильным следом плоскости (a W). Точки, в которых пересекаются два следа, называют точками схода следов (a x, a y, a z). На рис. 4.2, б показано задание плоскости a следами на эпюре. ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ Плоскость общего положения - это плоскость. не параллельная и не перпендикулярная ни одной из плоскостей проекций (рис. 4.1, 4.2).
Плоскости уровня Плоскость уровня - плоскость, параллельная какой-либо плоскости проекций и перпендикулярная двум другим плоскостям проекций.
Плоскость, параллельная горизонтальной плоскости проекций, называется горизонтальной плоскостью.
На рис. 4.3 плоскость, заданная треугольником ABC,является горизонтальной, т.к. ABC ║ H, ABC ^ V и W. А′В′С′ - натуральная величина треугольника.
Плоскость, параллельная фронтальной плоскости проекций, называется фронтальной плоскостью. На рис. 4.4 плоскость ABC является фронтальной, т.к. ABC ║ П2, ABC ^ П1 и П3. А ″ В ″ С ″ - натуральная величина треугольника.
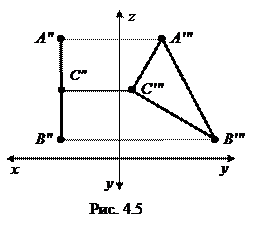
Плоскость, параллельная профильной плоскости проекций, называется профильной плоскостью. На рис. 4.5 плоскость ABC является профильной, т.к. ABC ║ П3, ABC ^ П1 и П2. А ″′ В ″′ С ″′ - натуральная величина треугольника.
Проецирующие плоскости
Плоскость, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей плоскостью (рис. 4.6).
Плоскость, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей плоскостью (рис. 4.7).
Плоскость, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей плоскостью (рис. 4.8).
ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ Линии уровня плоскости Линии уровня плоскости - прямые, принадлежащие заданной плоскости и параллельные какой - либо плоскости проекций.
Фронталь плоскости - прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций. На рис. 4.10 – прямая f. Профильная прямая плоскости - прямая, принадлежащая плоскости и параллельная профильной плоскости проекций. На рис. 4.10 – прямая w.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Перечислите способы задания плоскости. 2. Что называют следом плоскости? 3. Как определить положение плоскости относительно плоскостей проекции? 4. Как определить принадлежность точки заданной плоскости? 5. Как определить принадлежность прямой заданной плоскости? 6. Какие главные линии плоскости вы знаете? 7. Плоскость α, заданная треугольником АВС,...
- фронтальная - фронтально-проецирующая - общего положения -горизонтальная -профильная
8. Плоскость α, заданная следами,...
- фронтальная - профильно-проецирующая - общего положения - горизонтальная - профильная
9. Плоскость α, заданная следами,...
- фронтально-проецирующая - горизонтально-проецирующая - общего положения - горизонтальная - профильная
10. Плоскость α, заданная пересекающимися прямыми а и в,...
- профильно-проецирующая - общего положения - горизонтальная - профильная
11. Плоскость α, заданная треугольником АВС,...
- профильно-проецирующая - общего положения - горизонтальная - профильная
12. Плоскость α, заданная треугольником АВС,...
- фронтальная - общего положения - горизонтальная - профильная
13. Плоскости α, заданной треугольником KMN, принадлежит точка...
- А - В - С - Д - Е
14. Плоскости α, заданной треугольником KMN, принадлежит точка...
- А - В - С - Д - Е
15. Горизонталью плоскости α, заданной параллельными прямыми а и в, является прямая...
- с - d - m - n
ЗАНЯТИЕ 4 ПОЗИЦИОННЫЕ ЗАДАЧИ
Позиционные задачи - это задачи, решение которых дает ответ на вопрос о взаимном расположении геометрических фигур.
УСЛОВИЯ ПЕРПЕНДИКУЛЯРНОСТИ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
1. Прямые перпендикулярны, если одну из них можно заключить в плоскость, перпендикулярную другой прямой. 2. Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. 3. Плоскости перпендикулярны, если одна их них содержит прямую, перпендикулярную другой плоскости.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Условия параллельности и перпендикулярности прямых и плоскостей 2. Как построить точку пересечения прямой и плоскости частного положения? 3. Как построить линию пересечения двух плоскостей, если одна из них частного положения? 4. Как построить точку пересечения прямой общего положения и плоскости общего положения? 5. Как определить видимость линий при взаимном пересечении плоскостей?
- 1 - 2 - 3 7. Какой участок прямой l на фронтальной плоскости проекций является невидимым?
- 1 - 2 - 2 - 3
8. Линией пересечения плоскостей ABC и заданной пересекающимися прямыми а и в, является …
- 1 - 2 - 3 - 4
9. Какой участок плоскости ABC на горизонтальной плоскости проекций является невидимым?
- А12 - 12ВС - А34 - 34ВС
ЗАНЯТИЕ 5 СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА Метрические задачи - это задачи, связанные с определением различных величин геометрических фигур (натуральных величин отрезка и плоскости, величины углов, кратчайших расстояний и т.д.). В начертательной геометриизадачи решаются графически. Количество геометрических построений и их характер при этом определяется не только сложностью задачи, но и в значительной степени зависят от того, с какими проекциями приходиться иметь дело (удобными или неудобными). Задачи решаются значительно проще в случае частного положения геометрической фигуры относительно плоскости проекций. Переход от общего положения к частному осуществляют, используя способыпреобразования чертежа. Четыре основные задачи преобразования: 1. Преобразовать чертеж так, чтобы прямая общего положения заняла положение прямой уровня. 2. Преобразовать чертеж так, чтобы прямая общего положения заняла положение проецирующей прямой. 3. Преобразовать чертеж так, чтобы плоскость общего положения заняла положение проецирующей плоскости. 4. Преобразовать чертеж так, чтобы плоскость общего положения заняла положение плоскости уровня. Задача 1.
Задача 2. На рис. 6.3 задан отрезок общего положения АВ. Для того, чтобы он занял проецирующее положение, его сначала нужно перевести в положение уровня. Выполнив для этого необходимые действия (см. задачу 1), введем еще одну новую плоскость проекций Н1, которой отрезок будет перпендикулярен.
Задача 3.
Задача 4.
СПОСОБ ВРАЩЕНИЯ ВОКРУГ ОСИ, Задача 1.
Для того, чтобы отрезок АВ занял положение уровня, переместим А по окружности так, чтобы В″А1″ ║ х. Положение А1′ будет находится на пересечении линии связи, проведенной от А1″ и горизонтальной прямой от А′ (проекции окружности). Таким образом, отрезок АВ занял положение горизонтали (А1″В″ - натуральная величина АВ, угол между А1′В′ и х является действительной величиной угла наклона АВ к плоскости V).
Задача 2.
Таким образом, отрезок АВ занял фронтально-проецирующее положение.
Задача 3. На рис. 6.8 задана плоскость общего положения АВС. Для того чтобы она заняла проецирующее положение, зададим какую-либо линию уровня плоскости, например горизонталь плоскости h. Пусть ось вращения i1 ^ Н и проходит через точку С. Переведем h во фронтально-проецирующее положение путем вращения вокруг оси i1. При этом она повернется на угол φ. На такой же угол вращают остальные точки плоскости А, В, С. Таким образом, получим фронтально-проецируюшую плоскость А1В1С (угол между В1″С″А1″ и х является действительной величиной угла наклона АВС к плоскости Н).
Задача 4. На рис. 6.9 задана плоскость общего положения АВС. Для того чтобы она заняла положение плоскости уровня, ее сначала нужно перевести в проецирующее положение. Выполнив для этого необходимые действия (см. задачу 3), введем еще одну ось вращения i2 ^ V, которая проходит через точку В. Провращаем плоскость А1В1С так, чтобы А2″В1″С2″ ║ x. Таким образом, плоскость займет положение горизонтальной плоскости (А2′В1′С2′ - натуральная величина АВС).
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Какие способы преобразования чертежа вы знаете? Их сущность. 2. Сколько и в какой последовательности нужно ввести дополнительных плоскостей для преобразования прямой общего положения в проецирующее? 3. Каким образом нужно выбрать ось вращения при применении способа вращения вокруг оси, перпендикулярной к плоскости проекций, для упрощения построений? 4. Какие построения необходимо выполнить, чтобы плоскость общего положения преобразовать в проецирующее, используя способ вращения вокруг оси, перпендикулярной к плоскости проекций? 5. Как определить натуральную величину отрезка и углы его наклона к плоскостям проекций с помощью способов преобразования чертежа? 6. В какой плоскости перемещается точка при вращении ее вокруг оси, перпендикулярной фронтальной плоскости проекции? - в плоскости, параллельной V - в плоскости, параллельной H - в плоскости, параллельной W
7. В какой плоскости происходит вращение точек отрезка АВ?
- в плоскости, параллельной V - в плоскости, параллельной H - в плоскости, параллельной W
8. Какая проекция отрезка АВ является его натуральной величиной?
- А″В″ - А′В′ - А1″В1″ - А1′В1′
- метод перемены плоскостей - метод прямоугольного треугольника - метод вращения
10. Какая проекция треугольника АВС является его натуральной величиной?
- А″В″С″ - А′В′С′ - А1″В1″С1″ - А1′В1′С1′ 11. Для того, чтобы перевести треугольник АВС в проецирующее положение ось х1 задают…
- параллельно В′С′ - перпендикулярно А′H′ - перпендикулярно А″H″ - произвольно
ЗАНЯТИЕ 6 КРИВЫЕ ЛИНИИ Кривую линию можно представить как траекторию точки, перемещающейся в пространстве или на плоскости, Кривые линии могут быть плоские, т.е. такие, все точки которых принадлежат одной плоскости и пространственные, точки которых не принадлежат одной плоскости. Примерами плоских кривых являются: окружность, эллипс, парабола. Примером пространственной кривой является винтовая линия.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 696; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.012 с.) |

 - принадлежность;
- принадлежность; - логическое следствие.
- логическое следствие. Дано: плоскость α;
Дано: плоскость α;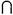 α = А α. Аналогично, выбрав произвольную точку В и построив луч SВ, получим В α.
α = А α. Аналогично, выбрав произвольную точку В и построив луч SВ, получим В α.
 - только горизонтальной плоскости проекции
- только горизонтальной плоскости проекции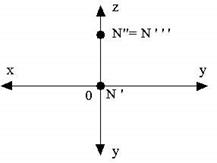 - только горизонтальной плоскости проекции
- только горизонтальной плоскости проекции - оси х
- оси х
 - только горизонтальной плоскости проекции
- только горизонтальной плоскости проекции


 Прямая уровня – это прямая, параллельная одной из плоскостей проекций.
Прямая уровня – это прямая, параллельная одной из плоскостей проекций.






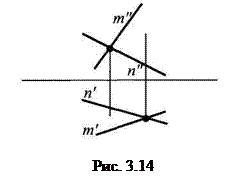
 На рис. 3.16 изображено:
На рис. 3.16 изображено: - рис. а)
- рис. а) 7. На каком чертеже прямая а является прямой общего положения,?
7. На каком чертеже прямая а является прямой общего положения,? 9. На каком чертеже прямые m и n является пересекающимися, скрещивающимися?
9. На каком чертеже прямые m и n является пересекающимися, скрещивающимися? - рис. в)
- рис. в)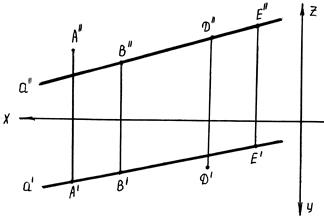 - А и D
- А и D
 След плоскости - прямая, по которой пересекаются плоскость с плоскостями проекций (рис. 4.2).
След плоскости - прямая, по которой пересекаются плоскость с плоскостями проекций (рис. 4.2).

 Проецирующая плоскость - плоскость, перпендикулярная какой-либо плоскости проекций.
Проецирующая плоскость - плоскость, перпендикулярная какой-либо плоскости проекций.

 Горизонталь плоскости - прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций. На рис. 4.10 – прямая h.
Горизонталь плоскости - прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций. На рис. 4.10 – прямая h. 



 - фронтальная
- фронтальная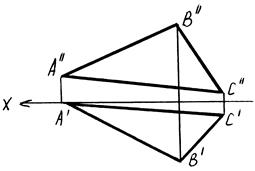 - фронтальная
- фронтальная - фронтально-проецирующая
- фронтально-проецирующая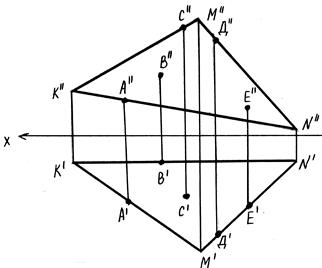


 6. Точкой пересечения прямой l и плоскости, заданной параллельными прямыми а и в является …
6. Точкой пересечения прямой l и плоскости, заданной параллельными прямыми а и в является …


 На рис. 6.2 задан отрезок общего положения АВ. Для того, чтобы он занял положение прямой уровня, новую ось нужно выбрать параллельно какой-либо проекции отрезка. Пусть х1 ║ А′В′, тогда положение отрезка будет параллельно новой фронтальной плоскости проекций V1. Построим на плоскости V1 новые проекции точек (концов отрезка) А1″ и В1″ (см. рис. 6.1 б). Таким образом, осуществив переход от старой системы плоскостей проекций
На рис. 6.2 задан отрезок общего положения АВ. Для того, чтобы он занял положение прямой уровня, новую ось нужно выбрать параллельно какой-либо проекции отрезка. Пусть х1 ║ А′В′, тогда положение отрезка будет параллельно новой фронтальной плоскости проекций V1. Построим на плоскости V1 новые проекции точек (концов отрезка) А1″ и В1″ (см. рис. 6.1 б). Таким образом, осуществив переход от старой системы плоскостей проекций  к новой системе
к новой системе  , отрезок АВ занял положение фронтали (А1″В1″ - натуральная величина АВ, угол между А1″В1″ и х1 является действительной величиной угла наклона АВ к плоскости Н).
, отрезок АВ занял положение фронтали (А1″В1″ - натуральная величина АВ, угол между А1″В1″ и х1 является действительной величиной угла наклона АВ к плоскости Н).  Поэтому, выбираем новую ось х2 ^ А1″В1″. Чтобы получить новую проекцию отрезка А1′В1′, величину координаты «y» берем из предыдущей системы плоскостей проекций
Поэтому, выбираем новую ось х2 ^ А1″В1″. Чтобы получить новую проекцию отрезка А1′В1′, величину координаты «y» берем из предыдущей системы плоскостей проекций  , отрезок АВ занял горизонтально-проецирующее положение.
, отрезок АВ занял горизонтально-проецирующее положение.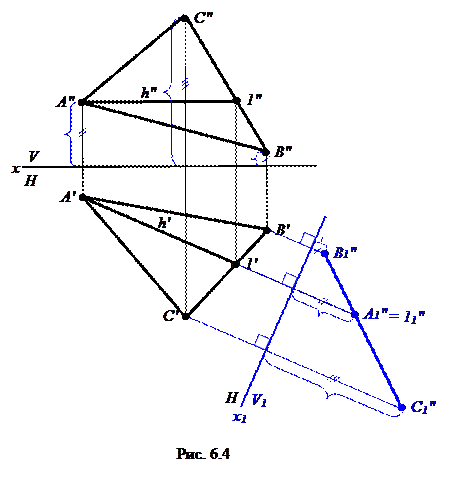 На рис. 6.4 задана плоскость общего положения АВС. Для того чтобы она заняла проецирующее положение, новую ось нужно выбрать перпендикулярно какой-либо линии уровня плоскости, например горизонтали плоскости. Тогда х1 ^ h′. В этом случае положение плоскости АВС будет перпендикулярно новой фронтальной плоскости проекций V1. Таким образом, осуществив переход от старой системы плоскостей проекций к новой
На рис. 6.4 задана плоскость общего положения АВС. Для того чтобы она заняла проецирующее положение, новую ось нужно выбрать перпендикулярно какой-либо линии уровня плоскости, например горизонтали плоскости. Тогда х1 ^ h′. В этом случае положение плоскости АВС будет перпендикулярно новой фронтальной плоскости проекций V1. Таким образом, осуществив переход от старой системы плоскостей проекций к новой  На рис. 6.5 задана плоскость общего положения АВС. Для того чтобы АВС заняла положение уровня, ее сначала нужно перевести в проецирующее положение. Выполнив для этого необходимые действия (см. задачу 3), введем еще одну новую плоскость проекций Н1, которой плоскость будет параллельна. Поэтому, выбираем новую ось х2 ║ А1″В1″С1″. Чтобы получить новую проекцию плоскости А1′В1′С1′, величину координаты «y» берем из предыдущей системы плоскостей проекций
На рис. 6.5 задана плоскость общего положения АВС. Для того чтобы АВС заняла положение уровня, ее сначала нужно перевести в проецирующее положение. Выполнив для этого необходимые действия (см. задачу 3), введем еще одну новую плоскость проекций Н1, которой плоскость будет параллельна. Поэтому, выбираем новую ось х2 ║ А1″В1″С1″. Чтобы получить новую проекцию плоскости А1′В1′С1′, величину координаты «y» берем из предыдущей системы плоскостей проекций  На рис. 6.6 задан отрезок общего положения АВ. Обозначим i1 - ось вращения. Пусть i1 ^ V и проходит через точку В. Тогда при вращении вокруг оси В останется на месте, А будет перемещаться в плоскости, перпендикулярной i1, а следовательно параллельной V. Таким образом, окружность, по которой движется точка, на плоскость V проецируется без искажения, а на плоскость Н – в отрезок, параллельный оси х.
На рис. 6.6 задан отрезок общего положения АВ. Обозначим i1 - ось вращения. Пусть i1 ^ V и проходит через точку В. Тогда при вращении вокруг оси В останется на месте, А будет перемещаться в плоскости, перпендикулярной i1, а следовательно параллельной V. Таким образом, окружность, по которой движется точка, на плоскость V проецируется без искажения, а на плоскость Н – в отрезок, параллельный оси х. На рис. 6.7 задан отрезок общего положения АВ. Для того, чтобы АВ занял проецирующее положение, его сначала нужно перевести в положение уровня. Выполнив для этого необходимые действия (см. задачу 1), введем еще одну ось вращения i2 ^ Н. Переместим А1′ и В′ по окружности так, чтобы А2′ В2′ ^ х. Положение А2″ и В2″ будет находится на пересечении линии связи, проведенной от А2′ В2′ и горизонтальной прямой от В″А1″ (проекции окружности, по которой двигались А1′ и В′).
На рис. 6.7 задан отрезок общего положения АВ. Для того, чтобы АВ занял проецирующее положение, его сначала нужно перевести в положение уровня. Выполнив для этого необходимые действия (см. задачу 1), введем еще одну ось вращения i2 ^ Н. Переместим А1′ и В′ по окружности так, чтобы А2′ В2′ ^ х. Положение А2″ и В2″ будет находится на пересечении линии связи, проведенной от А2′ В2′ и горизонтальной прямой от В″А1″ (проекции окружности, по которой двигались А1′ и В′).



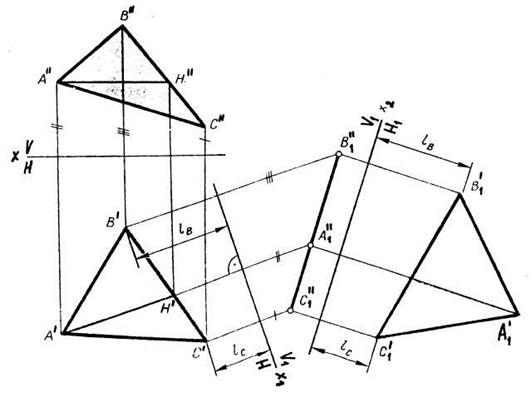 9. Какой метод использован для определения натуральной величины треугольника АВС?
9. Какой метод использован для определения натуральной величины треугольника АВС?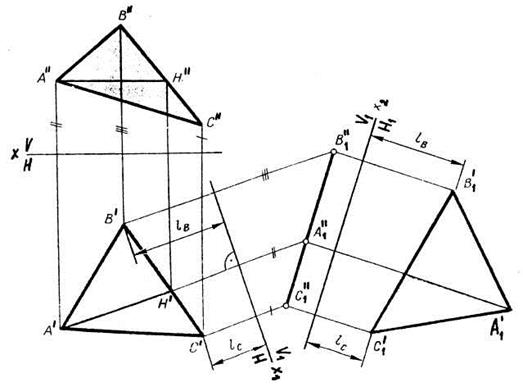

 Для построения ортогональных проекций кривой (простран
Для построения ортогональных проекций кривой (простран 


