
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоскостью частного положенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
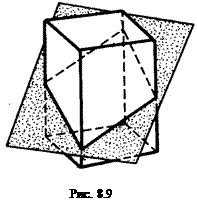
Пересечение многогранников плоскостью частного положения При пересечении поверхности с плоскостью получается плоская фигура, называемая сечением. Под сечением понимают ту часть секущей плоскости, которая находится внутри рассеченного тела. Плоскости, с помощью которых получается сечение, называют секущими. Фигура сечения многогранника — многоугольник, число сторон которого равно числу граней, пересекаемых плоскостью (рис. 8.9). Вершинами этого многоугольника являются точки пересечения ребер с секущей плоскостью, а сторонами — линии пересечения граней с секущей плоскостью. Рассмотрим пример решения такой задачи.
Пример. Пересечение пирамиды плоскостью частного положения. На рис. 8.10 даны три проекции четырехгранной пирамиды. Секущая плоскость задана следом αV и является фронтально-проецирующей. Сечение будет иметь вид четырехугольника. Фронтальная проекция сечения совпадает с фронтальной проекцией секущей плоскости αV. Обозначим фронтальные проекции вершин сечения (точек пересечения ребер с секущей плоскостью) - 1″, 2″, 3″, 4″. Проекция 3″ заключена в скобки, т.к. является невидимой. Горизонтальные и профильные проекции точек находят из условия принадлежности их ребрам пирамиды.
Рис. 8.10
Пересечение поверхностей вращения Плоскостью частного положения
Пример. Пересечение конуса плоскостью частного положения. На рис. 8.12 даны три проекции конуса. Секущая плоскость задана следом αV и является фронтально-проецирующей. Сечение будет иметь вид эллипса. Обозначим большую ось эллипса АВ, малую ось- CD. CD делит пополам АВ. Фронтальная проекция сечения совпадает с фронтальной проекцией секущей плоскости αV. Обозначим фронтальные проекции А″, В″, в середине А″В″ - C″, D″, а также 1″, 2″, лежащие на профильных очерковых образующих. Горизонтальные проекции точек находят, как лежащие на окружностях поверхности конуса, профильные – координатным способом.
Рис. 8.12 ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Какая линия называется кривой? Примеры кривых линий. 2. Как построить ортогональные проекции кривой линии? 3. Что называется поверхностью, образующей? 4. Приведите краткую классификацию поверхностей? 5. Приведите примеры поверхностей вращения. 6. Приведите примеры гранных поверхностей. 7. Какая поверхность называется проецирующей? 8. Как построить ортогональные проекции поверхности. 9. Сформулируйте условие принадлежности точки поверхности. 10. Что называется сечением, секущей плоскостью? 11. Какой фигурой является сечение многогранника и поверхности вращения? 12. Поверхности цилиндра принадлежит точка…
13. Поверхности конуса принадлежит точка (точки)…
14. Поверхности призмы принадлежит точка…
15. Поверхности пирамиды принадлежит точка…
16. Найдите соответствие между наглядным изображением поверхности, пересеченной проецирующей плоскостью и ее ортогональными проекциями в столбцах таблицы.
Ответ: 1-; 2 -; 3 -.
ЗАНЯТИЕ 7 ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 1031; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.236.144 (0.006 с.) |



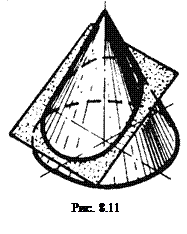 Фигура сечения поверхности вращения плоскостью (рис. 8.11) в общем случае - плоская кривая линия (окружность, эллипс и т. п.). Рассмотрим пример решения такой задачи.
Фигура сечения поверхности вращения плоскостью (рис. 8.11) в общем случае - плоская кривая линия (окружность, эллипс и т. п.). Рассмотрим пример решения такой задачи.





 A
A

 B
B

 C
C



