
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконечно малые функции и их основные свойства.Содержание книги
Поиск на нашем сайте
ОПРЕДЕЛЕНИЕ: Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если Примеры. 1. Функция 2. 3. 4. 5. 6. 7. 8.
2. Функция f(x) = tg x – бесконечно малая при x →0. 3. f(x) = ln (1+ x)– бесконечно малая при x →0. 4. f(x) = 1/ x – бесконечно малая при x →∞.
Связь бесконечно малых величин с пределами функций.
Теорема: Если функция
Доказательство: Докажем теорему для случая x→a. По условию функция имеет предел и
Выполняется
Или обозначив
Верна и обратная теорема:
Теорема: Если функцию можно представить как сумму числа
Основные свойства бесконечно малых функций 1. Теорема 1: Алгебраическая сумма (разность) двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая. 2. Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция. Из доказанной теоремы вытекают: Следствие 1. Если То Следствие 2. Если
3. Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция. Доказательство. Пусть ОПРЕДЕЛЕНИЕ: Функция Обозначение: Например: Определение бесконечно большой величины при
Не следует путать бесконечно большую переменную величину
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.13.127 (0.007 с.) |

 или
или  , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю. является бесконечно малой при x →1, так как
является бесконечно малой при x →1, так как  (см. рис.).
(см. рис.).
 имеет при x→a или при x →∞, предел равный
имеет при x→a или при x →∞, предел равный  ., то ее можно представить в виде суммы этого числа
., то ее можно представить в виде суммы этого числа  при x→a или при x →∞.
при x→a или при x →∞.
 . Это означает: что если для любого, даже сколь угодно малого положительного числа
. Это означает: что если для любого, даже сколь угодно малого положительного числа  , найдется такое положительное число
, найдется такое положительное число  (зависящее от
(зависящее от  ,
,  ), что для всех
), что для всех  и удовлетворяющих неравенству:
и удовлетворяющих неравенству:

 , имеем
, имеем  . А это собственно и значит, что
. А это собственно и значит, что  .
. и
и 
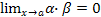 .
.
 . Тогда 1 /f(x) есть ограниченная функция. Поэтому дробь
. Тогда 1 /f(x) есть ограниченная функция. Поэтому дробь  есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.
есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая. называется бесконечно большой величиной при
называется бесконечно большой величиной при  , если для любого, даже сколь угодно большого положительного числа
, если для любого, даже сколь угодно большого положительного числа 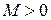 , найдется такое положительное число
, найдется такое положительное число  ,
,  ), что для всех
), что для всех  .
.
 при
при  бесконечно большая функция.
бесконечно большая функция.  при
при  бесконечно большая функция, причем
бесконечно большая функция, причем  , и
, и 
 запишем в краткой форме, его записать самим подробно!
запишем в краткой форме, его записать самим подробно!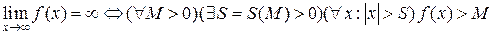
 или
или  , обе функции являются бесконечно большими.
, обе функции являются бесконечно большими. к
к  или по мере увеличения по модулю
или по мере увеличения по модулю 


