
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства бесконечно больших величинСодержание книги
Поиск на нашем сайте
1. Произведение б\б величины на функцию, предел которой отличен от нуля, есть величина б\б. 2. Сумма б\б величины и ограниченной функции есть величина б\б. 3. Частное от деления б\б величины на функцию, имеющую предел, есть величина б\б. Например: 1. если 2. Если 3. СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1 /f(x) является бесконечно малой при x→a. Примеры. 1. Ясно, что при x→+∞ функция y=x2+ 1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция 2. Можно доказать и обратную теорему. Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y= 1 /f(x) является бесконечно большой функцией.
Примеры. 1. 2. 3. Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A ≠ 0
ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ. ПРИЗНАКИ СУЩЕСТВОВАНИЯ ПРЕДЕЛА.
2. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
Пример. 3. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
Следствие 1. Постоянный множитель можно выносить за знак предела:
Следствие 2. Предел степени равен степени предела:
Пример: 4. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е. Примеры. 1.) 2.) 3.) Рассмотрим 5. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u (x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если
Смысл этой теоремы понятен из рисунка. 6. Если две функции f(x) и g(x) при всех значениях аргумента x удовлетворяют неравенству f(x)≥ g(x) и имеют пределы
ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ Первым замечательным пределом называется Вторым замечательным пределом: Число
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.166.195 (0.009 с.) |

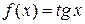 есть б\б величина при
есть б\б величина при  , функция
, функция  при
при  , то функция
, то функция 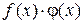 - б\б. (1 свойство)
- б\б. (1 свойство)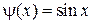 - ограниченная функция, то
- ограниченная функция, то  - б\б функция (2 свойство)
- б\б функция (2 свойство) является б\б функцией при
является б\б функцией при  – бесконечно малая при x→+∞, т.е.
– бесконечно малая при x→+∞, т.е.  .
. .
. .
. .
.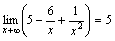 , так как функции
, так как функции 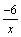 и
и  - бесконечно малые при x→+∞, то
- бесконечно малые при x→+∞, то 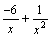 , как сумма бесконечно малых функций есть функция бесконечно малая. Функция же
, как сумма бесконечно малых функций есть функция бесконечно малая. Функция же  является суммой постоянного числа и бесконечно малой функции. Следовательно, по теореме 1 для бесконечно малых функций получаем нужное равенство.
является суммой постоянного числа и бесконечно малой функции. Следовательно, по теореме 1 для бесконечно малых функций получаем нужное равенство. .
.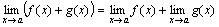
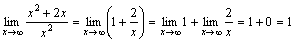 .
.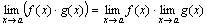 .
.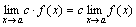 .
. .
. .
.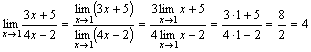 .
.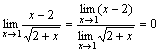 .
.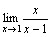 . При x→1 числитель дроби стремится к 1, а знаменатель стремится к 0. Но так как
. При x→1 числитель дроби стремится к 1, а знаменатель стремится к 0. Но так как 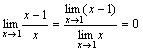 , т.е.
, т.е. 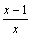 есть бесконечно малая функция при x→ 1, то
есть бесконечно малая функция при x→ 1, то  .
.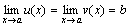 , то
, то  .
.
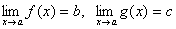 , то имеет место неравенство b≥c.
, то имеет место неравенство b≥c.
 или
или 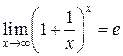
 . Точнее
. Точнее 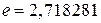 …, т.е является числом иррациональным. Играет весьма важную роль в математическом анализе. Широко используются логарифмы по основанию
…, т.е является числом иррациональным. Играет весьма важную роль в математическом анализе. Широко используются логарифмы по основанию  , называемые натуральными.
, называемые натуральными.


