
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратная функция. Композиция функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение: Функция
Если график обратной функции рассматривать в том же множестве
Обратимость Функции Определение: Функция
Геометрическим признаком однозначности функции является то, что прямые перпендикулярные оси
Композиция функции
Пример:
Основные элементарные функции
а) б) в) г) д) при
а) Разобьём весь график
выберем в качестве основного промежутка  и отобразим обратную функцию на этом промежутке, обозначим и отобразим обратную функцию на этом промежутке, обозначим 
 
б)

в)
Классификация функций
Элементарные функции – это функции получающиеся из основных элементарных, с помощью конечного числа последовательно выполненных арифметических операций и композиций
В классе элементарных функций выделяют алгебраические и трансцендентные
Алгебраические а) Многочлен или целая рациональная функция. При её образовании используются действия: «+», «-», «
б) Рациональные или дробно-рациональные функции. При их образовании используются действия: «+», «-», «
в) Иррациональные. При их образовании используются действия: «+», «-», « «
Все остальные функции не являющиеся алгебраическими являются трансцендентными
Предел функции.
Окрестности.
10. Пусть
Определение1.
Определение2.
Определение3. Окрестность точки x0
Ясно, что любая
20. Свойства окрестностей. 1) 2) Пересечение 2-х окрестностей точки снова является окрестностью этой точки. 3) Доказательство. x0
U  (x0) (x0)  U U  (x0) =: U (x0) =: U  (x0), (x0),
Где  =min{ =min{  ; ;  } }
(U
4) Свойство отделимости. Если x1, x2
Доказательство. x1, x2
U
Определение 4. Система (множество) окрестностей точки x0 (Ų) (элементы системы являются окрестности) называется фундаментальной, если
Пример1. U:= { U x0 система фундаментальная
Пример2. x0 U1(x0)
5)
Предельная точка множества.
Рассматриваем E
Определение. a
Множество всех предельных для E точек будет называться E’: x0
В любой окрестности предельной точки множества E содержится бесконечное число точек из E
Доказательство: U(x0), x0 Допустим, что в окрестности есть конечное число точек из E неравных x0. По свойству 3 у нас
U*(x0) = U'(x0)
Получается, что U*(x0) не содержит ни одной из точек x1, x2,…, xk
Из того, что U*(x0) не содержится ни одной из точек x1, x2,…, xk
Определение предела.
10. 1) f(x)=x+1, x 2) f(x)=
Определение. Под пределом функции понимается число P функции f(x) при x→x0, если значение функции становится как угодно близким к P, лишь только x из области определения становится достаточно близким к x0.
20. Определение (основное определение предела). Пусть f: X→Y, E Число p называется пределом функции f(x) при x→x0 на множестве E, если p=lim f(x) x→ x0,E
Геометрическая интерпретация а)
30. Определение предела на языке
Определение. Число з называется пределом функции f(x) при x→x0 на множестве E, если
Пример: y
|y-p| <
p=+
y>
Осуществляется перевод с языка окрестностей на язык неравенств можно дать определение предела через неравенства для конкретных вариантов.
x0 p=lim f(x) x→ x0,E
|x- x0| < где x
Общие свойства пределов.
10. Свойство 1.
Пусть f(x)  C C  R R  limC = C limC = C
x→ x0,  x0 x0  R R
Свойство 2. Единственность предела.
Пределом функции f(x) при x→x0 единственен.
Доказательство.
(от обратного)
Пусть p1=lim f(x)   U(p1) U(p1)  U'(x0): x U'(x0): x  U'(x0) U'(x0)  f(x) f(x)  U(p1) U(p1)
x→ x0,E и пусть p2=lim f(x) x→ x0,E где x Выберем U(p1) Если возьмем x =Ø =Ø
20. Сужение функции.
Определение. Пусть f: X→Y; функция
Свойство 3.
Если 1) lim f(x) = p; x→ x0,E 2) 3) x0
x→ x0,E1
Доказательство: По определению предела:
Тогда
x→ x0,E1
30. Связь между пределами функции на множестве и на его частях.
Свойство 4. Пусть x→ x0,E x0 x→ x0,E1 Доказательство следует из предыдущего свойства.
Свойство 5. Пусть U x→ x0,E следует, что x→ x0,E Доказательство:
x Свойство 6. Пусть E = E1 U E2, Тогда x→ x0,E x→ x0,E1 x→ x0,E2
пределов.
40. Ограниченная функция.
Определение 1. f: E→R. Функция f называется ограниченной сверху (снизу, просто ограниченной), если множество её значений ограничено сверху (снизу, просто).
Например: y = [1; +
Определение 2. Функция называется ограниченной сверху (снизу, вообще на E) при x→ x0 , если
Свойство 7. Если существует конечный предел lim f(x) =: p, x→ x0,E то функция f ограниченна при x→ x0 на множестве E.
x→ x0,E f(x)
50. Предел последовательности.
Определение. Число p называется пределом xn при n→ + Например: xn =
|
Определение. Последовательность называется сходящейся если она имеет конечный предел.
Свойство 8. Всякая сходящаяся последовательность ограниченна. Доказательство. lim xn =:p n→ +
По свойству 7 xn - ограниченна при n→ +
A = min{x1,x2,…xn, a} B = max{b, x1,x2,…xn}
60. Предел сложной функции.
Свойство 9. Пусть: 1) f: E
2) x→ x0,E y→ y0,G
3) y0 lim g(f(x)) = p (5) x→ x0,E
(5) x→ x0,E y→ lim f(x) x→ x0,E
Доказательство. Возьмем (6) По условию 2)1 выбрали окрестность y0 (8)
Возьмем x 1) y
2) Так как y0
Итак, в любом случае Рассмотрим пример, показывающий что при несоблюдении свойства 9 условия 3 формулы (5) может привести к ошибке f(x)=y0; g(y)= limg(f(x))= \\g(y0)=0\\ =0 x→ x0 Вычислим формально по формуле (5) (5) x→ x0,E y→ lim f(x) x→ x0,E
Ошибка заключается в том, что не выполнено условие 3 свойства 9 т.к. y0 является значением функции при
Следствие 1. Пусть lim f(x) =:p, то для x→ x0,E n→
n→
Доказательство. xn=x(n); lim f(x(n)) n→
Условие 3 свойства 9 выполнено, т.к. предел внутренней функции не является не является ее значением.
Следствие 2.
x→ x0,E n→
n→
Доказательство. yn = y(n) является сужением функции f(xn) (по свойству 3)
Следствия 1 и 2 часто используют для доказательства отсутствия пределов.
Пример: Рассмотрим функцию y=sin Рассмотрим lim sin x→0
1) xn = lim sin n→
2) x | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 называется обратной к
называется обратной к  , если
, если  и каждому элементу
и каждому элементу  она сопоставляет
она сопоставляет  такое, что
такое, что  . Итак по определению имеем, что
. Итак по определению имеем, что 
 , то
, то  и
и  поменяются ролями. График обратной функции с аргументом
поменяются ролями. График обратной функции с аргументом 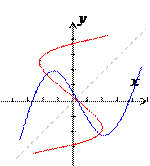
 пересекают её график не более чем в одной точке. Поэтому признак однозначности обратной функции и признак обратимости прямой функции это то, что прямые перпендикулярные оси
пересекают её график не более чем в одной точке. Поэтому признак однозначности обратной функции и признак обратимости прямой функции это то, что прямые перпендикулярные оси  ,
,  ,
,  такую функцию называют композицией функции и обозначают
такую функцию называют композицией функции и обозначают 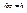 или
или 

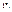 Постоянная функция:
Постоянная функция: 
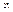 Степенная функция:
Степенная функция: 




 учитывается, что
учитывается, что 
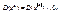
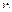 Показательная функция:
Показательная функция: 
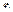 Логарифмическая функция:
Логарифмическая функция: 
 Тригонометрические функции:
Тригонометрические функции:
 Обратные тригонометрические функции:
Обратные тригонометрические функции: на промежутки монотонности
на промежутки монотонности  ...
...

 - радианная мера угла,
- радианная мера угла,  которого равен
которого равен 
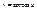


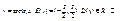

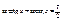

 »
»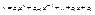
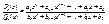
 »
»



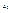
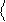



 (-
(- 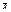 называется любое численное множество, содержащее некоторую
называется любое численное множество, содержащее некоторую  U1(x0)
U1(x0) 

 x2
x2






 (x0)} = {x0-
(x0)} = {x0-  , x0 +
, x0 +  U
U  (x0)
(x0)  (x0)…
(x0)… U'(x0),
U'(x0), x→0 f(x)→
x→0 f(x)→  (x0 является предельной для E)
(x0 является предельной для E)

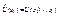 - проколотая окрестность
- проколотая окрестность - окрестностей.
- окрестностей.






 , чего быть не может.
, чего быть не может. : X1→Y называется сужением функции f на множестве X1 если X1
: X1→Y называется сужением функции f на множестве X1 если X1 




 (x0) – фиксированная окрестность, а f: E→R, тогда из
(x0) – фиксированная окрестность, а f: E→R, тогда из 






 xn
xn  ). По условию 2)2
). По условию 2)2  (7)
(7) 



 lim f(x) = p;
lim f(x) = p; → 0 при n→
→ 0 при n→  +2
+2  n) = 1
n) = 1 =
= 


