Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий (Б-К). Существование конечного предела функции. ⇐ ПредыдущаяСтр 4 из 4
Пусть f: E → R, x0 x→ x0,E достаточно, чтобы т.е. в точках достаточно близких к x0 значение функции отличается как угодно мало
Доказательство.
Дано (1), доказать (2) lim f(x) =: p x→ x0,E Возьмем Поэтому, для
Выполнено (2), доказать (1) Воспользуемся критерием существования lim f(x) на языке последовательностей ( Возьмем Возьмем Тогда x Тогда для Следовательно | f(xn) – f(xm) | < Но из
3.15. Сравнение функции при x→ x0 , E. (В этом параграфе все функции однозначны)
10. Определение. Пусть f, g: E → R, x0 Функция f(x) называется б.м.ф. по сравнению с g(x) при x→ x0 , E (б.б.ф), если f(x) = В случае, если такое представление возможно и lim
Обозначение: f(x) ~ g(x) x→ x0,E б.м.ф. f(x): f(x) = 0*g(x)
20. Б.м.ф. по сравнению с другими при x→ x0 , E.
Если g(x) x→ x0,E
Пример.
1) x2 = 0(x) при x → 0 lim x → 0 x → 0
2) sin2 x * sin lim x → 0 x → 0
Замечание. В записи f(x) = 0(g(x)) при x→ x0, E. Правая часть не означает конкретную функцию, а лишь означает, что речь идет о б.м.ф. при x→ x0
Свойства б.м.ф. 1) -0(g(x)) = 0(g(x)) 2) 0(g(x)) + 0(g(x)) = 0(g(x)) 3) h(x)*0(g(x)) = 0(h*g)
Доказательство (3-его св-ва) Пусть f(x) = 0(g(x)) при x→ x0, E. Это значит, что f(x) = x→ x0, E. Тогда h(x)*f(x) = h(x)*
h(x)*
30. Б.б.ф. по сравнению с другими при x→ x0, E.
f(x) – б.б.ф. по сравнению с g(x) при x→ x0 Так что x является б.б.ф. по сравнению с x2 при x → 0
40. Функции ограниченные по сравнению с другими.
Определение. f(x) называется ограниченной по сравнению g(x) при x→ x0, E, если f(x) =
Обозначение: f(x) = 0(g(x)) – ограниченная функция
Пример. x*sin x при x→ + x*sin x =
sin x – ограниченная функция.
Требование данного поределения x
Свойства ограниченной функции. 1) Если x→ x0,E f(x) = 0(g(x)) при x→ x0
2) 0(g(x)) + 0(g(x)) = 0(g(x))
Замечание. Если одновременно выполняется, что f(x) = 0(g(x)) и g(x) = 0(f(x)) при x→ x0 , то говорят, что f(x) и g(x) одного порядка.
Обозначение: f(x) = 0*(g)
Пример. f(x) = x g(x) = lim lim
50. Эквивалентные функции.
Свойства: 1) Если g(x) f ~ g означает lim
2) Утверждение, что f ~ g при x→ x0 , E f(x) = g(x) + 0(g(x)) при x→ x0 , E
Доказательство. f(x) ~ g(x) при x→ x0 , E f(x) = Тогда можно записать f(x) = (1 + f(x)= g(x) + f(x) = g(x) + 0(g(x))
3) Отношение эквивалентности функции при x→ x0 обладает свойствами: a) рефлексивность (отображательность) – т.е. x→ x0 б) симметричность f(x) ~ g(x) в) транзитивность f(x) ~ g(x), g(x) ~ h(x)
Доказательство. f(x) ~ g(x) g(x) ~ h(x) f(x) =
4) Если f(x) ~ f1(x), g(x) ~ g1(x) при x→ x0 , E, то: а) f(x)*g(x) ~ f1(x)*g1(x) б) при g(x),g1(x)
5) Если f ~ g x→ x0 , E, то x→ x0,E x→ x0,E x→ x0,E (при условии существования хотя бы одного из них).
Доказательство. f(x) ~ g(x) (*) x→ x0,E Пусть x→ x0,E из (*) следует g ~ f т.е. g = lim g(x) = lim (
1) Если f(x) ~ f1(x), g(x) ~ g1(x) при x→ x0 , E, то: а) б) g(x), g1(x)
При вычислении пределов произведения, частного, множители (делимое и делитель) можно заменить эквивалентными выражениями, прмчем это не повлияет ни на существование предела, ни на его значение.
Пример: lim x → 0 x → 0 x → 0
tg x ~ x
7) Если а) f(y) ~ g(y) при y → b, G б) y: E → G, a x → a в) b (т.е. если b
Тогда f(y(x)) ~ g(y(x)) x → a, E
Примеры: sin y ~ y, y → 0; sin x3 ~ x3, x → 0; 1 – cos x = 2sin2
1 – cos x ~ x → 0 lim
Замечание. Если lim f(x) = p, то f(x) ~ p x→ x0,E
lim x→ x0,E
Замечание. При вычислении пределов в алгебраических суммах эквивалентность использовать нельзя.
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.82.167 (0.085 с.) |
 E
E  . Для того, чтобы
. Для того, чтобы  конечный lim f(x) (1) необходимо и
конечный lim f(x) (1) необходимо и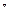 x
x 
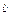 (x0)
(x0)  E выполняется | f(x
E выполняется | f(x  )| <
)| <  (2)
(2) (Необходимость)
(Необходимость)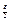
 (Достаточность)
(Достаточность) (x)*g(x), где
(x)*g(x), где  0 на E\{x0}, то утверждение, что f(x) – б.м.ф. по сравнению с g(x) при x→ x0 равносильно утверждению, что lim
0 на E\{x0}, то утверждение, что f(x) – б.м.ф. по сравнению с g(x) при x→ x0 равносильно утверждению, что lim  = 0
= 0 = lim x = 0
= lim x = 0 = 0(x*sin
= 0(x*sin  = lim
= lim  = sin x = 0
= sin x = 0
 g(x) = 0(f(x)) при x→ x0, E.
g(x) = 0(f(x)) при x→ x0, E. = 0(x)
= 0(x) C*| g(x)|
C*| g(x)|



 (x))*g(x), где (1 +
(x))*g(x), где (1 +  ~
~ 
 = // sin x ~ x // = lim
= // sin x ~ x // = lim 
 = 2sin
= 2sin