Взаимное положение прямых в пространстве. Определение видимости (метод конкурирующих точек).

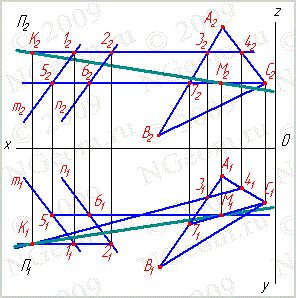
Прямые в пространстве могут быть ||, пересекающимися и скрещивающимися.

1. Если прямые в пространстве параллельны, то их одноименные проекции ||.

2. Если прямые пересекаются, то их одноименные проекции тоже пересекаются, а точка пересечения лежит на одной из линий связи.

3. Если для двух прямых не выполняются ни условия параллельности, ни условия пересечения, то они скрещивающиеся.

Определение видимости (метод конкурирующих точек):

В начертательной геометрии все предметы считаются непрозрачными. Вопрос о видимости на ортогональном чертеже того или иного предмета приходиться решать для каждой из проекций в отдельности, пользуясь методом конкурирующих точек.

Конкурирующими называются точки, лежащие на одном проецирующем луче.

Метод: Из двух совпавших на одной из проекции точек, принадлежащих разным геометрическим элементам, будет видна, другая проекция которой расположена дальше от оси проекции.

 

7. Теорема о проецировании прямого угла. Определение расстояния от точки до прямой частного положения.

При ортогональном проецировании прямой угол проецируется в прямой, если одна из его сторон параллельна плоскости проекции, а другая не перпендикулярна этой плоскости. Эту теорему применяют при решении задач на определение расстояния от точки до прямой частного положения.

Расстояние от точки до прямой определяется длиной перпендикуляра, опущенного из точки на прямую.
Если прямая параллельна плоскости проекции, т. е. является прямой частного положения (h | | П₁), то для того чтобы определить расстояние от точки А до прямой h необходимо опустить перпендикуляр из точки А на горизонталь h.

На ортогональном чертеже строим отрезок A₁M₁ перпендикулярно h₁. Далее на прямой h₁ откладываем отрезок M₁M₀ равный А₂В₂. Длину перпендикуляра АM можно найти способом прямоугольного треугольника А₁M₁M₀: |АM| = |А₁M₀|

Задание плоскости на эпюре.

Плоскость на Эпюре задается проекциями элемента, определяющими плоскость в пространстве, а именно:

А) проекциями трех точек, не лежащих на одной прямой;

Б) проекциями прямой и точки, не лежащей на этой прямой;

В) проекциями двух параллельных прямых;

Г) проекциями двух пересекающихся прямых;

Д) отсеком (плоскость, ограниченная линией)

Е) следами (Следами называются линии пересечения плоскости с плоскостями прекции. Чтобы построить следы плоскости нужно построить следы двух прямых, принадлежащих плоскости)

 

Главные линии плоскости

Из всех прямых необходимо выделить особо расположенные, имеющие важное значения как вспомогательные элементы при различных графических операциях:

1) Горизонталь плоскости – это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекции

2) Фронталь плоскости – это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекции.

3) Профиль плоскости – это прямая, лежащая в плоскости и параллельная П3.

 

10. Теорема о линии наибольшего наклона плоскости к плоскостям проекции.

Линия наибольшего наклона к плоскости (л. н. н.) - это прямая, лежащая в плоскости и образующая с плоскостью проекции наибольший угол. Она служит для измерения угла наклона плоскости, в которой она лежит, с соответствующей плоскостью проекции.

С точки зрения геометрии, линии, лежащие в плоскости и перпендикулярные линиям уровням плоскости.

Теорема 1. Горизонтальная проекция л н н к П1 ⊥ горизонтальной проекции горизонтали плоскости.

H принадлеж АВС (h2||Ox → h1)

C1O1⊥→ h1 – C2O2

Теорема 2.Фронтальная проекция л н н ⊥ фронтальной проекции фронтали плоскости.

 

Плоскости частного положения.

Плоскости уровня – это плоскости || одной из плоскостей проекции и ⊥ двум другим.

1. горизонтальная плоскость – это плоскость || П1

2. фронтальная плоскость – это плоскость || П2

3. профильная плоскость – это плоскость || П3.

Проецирующие плоскости. Основные свойства проецирующих плоскостей. Пример.

Проецирующие плоскости – это плоскости ⊥ одной из плоскостей проекции.

1. горизонтально проецирующая плоскость – это плоскость ⊥ П1

На горизонталь плоскости проекция горизонтально проецирующей плоскости проецируется в прямую (след), расположенную под углом к оси Ох. Фронтальный след П2 - оси х. Характерным для горизонтально проецирующей плоскости является то, что горизонтальная проекция любого геометрического элемента, лежащего в плоскости, всегда располагаются на горизонтальном следе плоскости.

2.фронтально проецирующая плоскость – это плоскость ⊥ фронтальной плоскости проекции.

3.профильно проецирующая плоскость – это плоскость ⊥ П3.

Основное свойство проецирующих плоскостей: одна проекция фигуры, принадлежащая проецирующей плоскости проецируется в отрезок прямой, совпадающий с одним следом плоскости (проецирующ).