
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проективная группа плоскости.Содержание книги Поиск на нашем сайте
Опр. 3.4.1. Группой преобразований некоторого множества X называется совокупность преобразований этого множества (не обязательно всех), которое образует группу относительно операции * – «композиция». Теорема 3.4.1. Множество всех проективных преобразований плоскости образует группу преобразований, которая называется проективной группой плоскости.
Замечание. При выбранном репере каждому проективному преобразованию соответствует матрица. Поэтому алгебраически группа проективных преобразований сводится к группе невырожденных матриц, соответствующих этим преобразованиям. Композиции преобразований соответствует произведение их матриц, обратному преобразованию – обратная матрица. Принцип Клейна. Любой группе преобразований соответствует своя геометрия, которая изучает те свойства фигур и те понятия, которые сохраняются при всех преобразованиях группы. Геометрией, которая соответствует проективной группе преобразований, является проективная геометрия. Она изучает те свойства фигур, и те понятия, которые сохраняются при всех проективных преобразованиях плоскости. Такие свойства и понятия называются проективными. Напри-мер, «прямая» является проективным понятием, а «несобственная точка», «параллельность прямых» не являются проективными понятиями
Определения и свойства. Опр. 4.1.1. Пусть точки A, B, C лежат на одной прямой. Число l называется простым отношением трех точек A, B, C, если = l . Это равносильно тому, что точка C делит отрезок AB в отношении l >0, если C лежит между A и B. Если же C лежит за пределами отрезка AB, то будет l < 0. Пишем l = (AB, C) или l = (ABC). Хотя не существует операции деления одного вектора на другой, мы будем писать l = /, если ½½. Простое отношение трех точек сохраняется при параллельном проецировании. Но легко показать, что оно не сохраняется при центральном проецировании, т.е. оно не является проективным понятием. Поэтому в проективной геометрии вводится сложное отношение 4 точек. Опр. 4.1.2. Сложным отношением четырех собственных точек A, B, C, D,лежащих на одной прямой, называется число (ABCD) = =: =. Будем также использовать такое обозначение сложного отношения: (AB, CD). Из 4-х букв можно образовать 24 перестановки. Однако различных значений сложных отношений 4 заданных точек одной прямой может быть только шесть. Теор 4. При перестановке пар A, B и C, D значение сложного отношения сохран-ся. По определению (CD, AB) = = = (AB, CD). Свойства сложных отношений. Пусть 1. (AB, CD) = n. Тогда 2. (AB, DC) = 1/n; 3. (AC, BD) = 1 – n; 4. (AD, BC) = 1 – =; 5. (AC, DB) =; 6. (AD, CB) =;
В каждом из пунктов 1 – 6 имеется по 4 равных значения для исходного значения сложного отношения. Возможны также частные случаи: а) D = C Þ (AB, CC) = 1; б) D = B Þ (AB, CB) = 0; в) D = A Þ(AB, CA) = ¥ . 36 Формулы сложных отношений. 1. Пусть точки A, B, C, D лежат на одной прямой и имеют в репере R координаты A (a 1, a 2), B (b 1, b 2), C (c 1, c 2), D (d 1, d 2). Требуется найти (ABCD). Найдем (ABCD) в частном случае, когда R = { A 1¥, A 2, E }. Тогда a 1/ a 2 = a, b 1/ b 2 = b, c 1/ c 2 = c, d 1/ d 2 = d, где a, b, c, d – обычные координаты на прямой. Поэтому
Можно показать, что по этой формуле выч-ся (ABCD)и в произв-ом репере на. Лемма. Координаты точки M Î в двух реперах R = { A 1, A 2, E } и R ¢= { A ¢1, A ¢2, E ¢} на связаны между собой формулами
x 2 = c 21 x ¢1+ c 22 x ¢2. Эта лемма д-ся дословно так же, как и аналогичная теорема для плоскости. Теор 4.2.1. Формула (4.2.1) имеет место в любом проективном репере.
a 2 = c 21 a ¢1+ c 22 a ¢2.
· · (ABCD) = –––––––––––––––: –––––––––––––––– = ––––––– : –––––––. · ·
2. Пусть на плоскости даны: проективная система координат R = { A 1, A 2, A 3, E }, прямая и на ней 4 точки A (a 1, a 2, a 3), B (b 1, b 2, b 3), C (c 1, c 2, c 3), D (d 1, d 2, d 3). Требуется найти (ABCD). Для этого нам потребуется следующая теорема. Теор 4.2.2. Сложное отношение сохраняется при центральном проецировании.
Спроецируем A, B, C, D из центра A 3 на прямую A 1 A 2. Проекции этих точек в репере R 3= { A 1, A 2, E 3} (E 3 – проекция точки E) будут иметь координаты (a 1, a 2),(b 1, b 2)(c 1, c 2), (d 1, d 2). Значит,
(ABCD) = () = ––––––: ––––––.
Вместо a 1, a 2 можно брать a 2, a 3 или a 1, a 3 ; это касается и координат других точек. Теорема 4.2.3. Сложное отношение сохраняется при любом проективном преобразовании плоскости.
3. Пусть в плоскости даны 4 точки A (a 1, a 2, a 3), B (b 1, b 2, b 3), C (c 1, c 2, c 3), D (d 1, d 2, d 3), лежащие на одной прямой. Тогда ci = l1 ai + m1 bi, di = l2 ai + m2 bi, i = 1, 2, 3, и из формулы (4.2.1) вытекает (ABCD) =: (4.2.4) 4. Теорема 4.2.4. Если A, B, C, D Î и точка D в репере R = { A, B, C } имеет координаты u 1 , u 2 , то (ABCD) = u 1/ u 2 .
Следствия. 1. " A, B, C Î "lÎ R $! D Î: (ABCD) =l. 2. Проективные координаты не зависят от выбора точки O (см. по 2.1).
|
|||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 403; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.101 (0.006 с.) |

 Пусть G – множество всех проективных преобразований плоскости , f Î G, g Î G. Пусть f задается реперами R и R ¢, g задается реперами R ¢ и R ². Тогда g * f переводит M (x 1, x 2, x 3) R в M ²(x 1, x 2, x 3) R², а значит, g * f – проективное преобразование. Роль единичного (нейтрального) элемента выполняет тождественное преобразование, которое, очевидно, является проективным. Обратное преобразование f –1 действует по правилу:
Пусть G – множество всех проективных преобразований плоскости , f Î G, g Î G. Пусть f задается реперами R и R ¢, g задается реперами R ¢ и R ². Тогда g * f переводит M (x 1, x 2, x 3) R в M ²(x 1, x 2, x 3) R², а значит, g * f – проективное преобразование. Роль единичного (нейтрального) элемента выполняет тождественное преобразование, которое, очевидно, является проективным. Обратное преобразование f –1 действует по правилу: M ¢(x 1, x 2, x 3) R¢ ® M (x 1, x 2, x 3) R, а значит, тоже является проективным. Так же легко показать, что операция * в G является ассоциативной.
M ¢(x 1, x 2, x 3) R¢ ® M (x 1, x 2, x 3) R, а значит, тоже является проективным. Так же легко показать, что операция * в G является ассоциативной.
 Докажем, например, свойство 2. По определению имеем:
Докажем, например, свойство 2. По определению имеем: (AB, DC) = = –1= =.
(AB, DC) = = –1= =.







 (ABCD) = (/):(/) = : = ––––––: ––––––. (4.2.1)
(ABCD) = (/):(/) = : = ––––––: ––––––. (4.2.1)
 x 1 = c 11 x ¢1+ c 12 x ¢2,
x 1 = c 11 x ¢1+ c 12 x ¢2, Пусть точки A, B, C, D имеют в репере R = { A 1¥, A 2, E } координаты A (a 1, a 2), B (b 1, b 2), C (c 1, c 2), D (d 1, d 2), а в репере R ¢= { A ¢1, A ¢2, E ¢} – A (a ¢1, a ¢2), B (b ¢1, b ¢2), C (c ¢1, c ¢2), D (d ¢1, d ¢2). Тогда (ABCD) вычисляется по формуле (4.2.1). Но, в соответствии с (4.2.2)
Пусть точки A, B, C, D имеют в репере R = { A 1¥, A 2, E } координаты A (a 1, a 2), B (b 1, b 2), C (c 1, c 2), D (d 1, d 2), а в репере R ¢= { A ¢1, A ¢2, E ¢} – A (a ¢1, a ¢2), B (b ¢1, b ¢2), C (c ¢1, c ¢2), D (d ¢1, d ¢2). Тогда (ABCD) вычисляется по формуле (4.2.1). Но, в соответствии с (4.2.2)
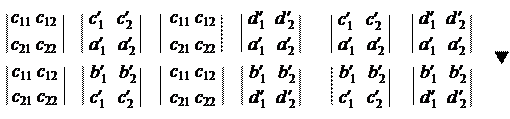 И это же выполняется для координат других точек. Подст-я(4.2.3) в(4.2.1) получаем
И это же выполняется для координат других точек. Подст-я(4.2.3) в(4.2.1) получаем Пусть точки A, B, C, D прямой проецируются из центра S в точки A ¢, B ¢, C ¢, D ¢ прямой. Пусть R = { A 1, A 2, E } – произвольный репер
Пусть точки A, B, C, D прямой проецируются из центра S в точки A ¢, B ¢, C ¢, D ¢ прямой. Пусть R = { A 1, A 2, E } – произвольный репер на, а A ¢1, A ¢2, E ¢ – проекции точек A 1, A 2, E из S на. Тогда R ¢= { A ¢1, A ¢2, E ¢} – репер на. Тогда согласно по 2.1 точки A ¢, B ¢, C ¢, D ¢ имеют в репере R ¢ такие же координаты, что и точки A, B, C, D в репере R. Из теоремы 4.2.1 вытекает, что (ABCD) = (A ¢ B ¢ C ¢ D ¢).
на, а A ¢1, A ¢2, E ¢ – проекции точек A 1, A 2, E из S на. Тогда R ¢= { A ¢1, A ¢2, E ¢} – репер на. Тогда согласно по 2.1 точки A ¢, B ¢, C ¢, D ¢ имеют в репере R ¢ такие же координаты, что и точки A, B, C, D в репере R. Из теоремы 4.2.1 вытекает, что (ABCD) = (A ¢ B ¢ C ¢ D ¢).

 Пусть f – проективное преобразование плоскости, которое задается реперами R и R ¢. Пусть точки A, B, C, D на прямой имеют координаты в репере R: A (ai), B (bi), C (ci), D (di), и пусть при преобразовании f они переходят в A ¢, B ¢, C ¢, D ¢. Тогда в репере R ¢: A ¢(ai), B ¢(bi), C ¢(ci), D ¢(di). Значит, (ABCD) = (A ¢ B ¢ C ¢ D ¢) .
Пусть f – проективное преобразование плоскости, которое задается реперами R и R ¢. Пусть точки A, B, C, D на прямой имеют координаты в репере R: A (ai), B (bi), C (ci), D (di), и пусть при преобразовании f они переходят в A ¢, B ¢, C ¢, D ¢. Тогда в репере R ¢: A ¢(ai), B ¢(bi), C ¢(ci), D ¢(di). Значит, (ABCD) = (A ¢ B ¢ C ¢ D ¢) . A (1, 0), B (0,1), C (1, 1), D (u 1, u 2) Þ l1= m1 =1, l2= u 1, m2= u 2 Þ
A (1, 0), B (0,1), C (1, 1), D (u 1, u 2) Þ l1= m1 =1, l2= u 1, m2= u 2 Þ Þ (ABCD) = u 1/ u 2 .
Þ (ABCD) = u 1/ u 2 .


