
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства расширенных плоскости и пространства.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Многие свойства принадлежности точек, прямых и плоскостей обычного евклидова пространства остаются и у расширенного пространства.
5. Если две точки прямой лежат в плос-и, то и вся прямая лежит в этой плоскости. 6. Через три точки, которые не лежат на одной прямой, можно провести плоскость и, притом, только одну. Для д-ва, напр, св-ва 1 необходимо рас-ть 3 возможных случ: а) данные точки собственные; б)одна точка собственая, а вторая – несобст; в) обе точки несобств. Однако принадлежность точек, прямых и плоскостей в расширенном пространстве обладает и некоторыми новыми свойствами. Например: 7. Любые две различные прямые, лежащие в одной плоскости, имеют общую точку и, притом, только одну. 8. Любая плоскость и прямая, которая не лежит в этой плоскости, имеют общую точку и, притом, только одну.
в) плоскость несобственная, а прямая собственная; в обоих случаях б) и в) общей явл. несобств. точка прямой.
24 Принцип двойственности на проективнойплоскости. Легко заметить, что свойства принадлежности на проективной плоскости обладают своеобразной симметрией. Например, свойства 1 и 7. Для того, чтобы эта симметрия стала более заметной, удобно ввести понятие инцидентности. Вместо выражения «точка принадлежит прямой» будем говорить «точка инцидентна прямой», а вместо «прямая проходит через точку» – «прямая инцидентна точке». Тогда свойства 1 и 7 можно переформулировать так:
1¢. Любые две различные точки инцидентны одной прямой и, притом, единственной. 7¢. Любые две различные прямые инцидентны одной точке и, притом, единственной. Такая же симметрия наблюдается и относительно других свойств. Таким образом, имеет место следующий принцип двойственности. Каждому утверждению на проективной плоскости относительно точек и прямых соответствует второе утверждение, которое получается из первого заменой слова «точка» на слово «прямая», а слова «прямая» на слово «точка». Второе утверждение называется двойственным первому и, если истинно первое утверждение, то и истинно и двойственное ему. В соответствии с этим принципом каждой фигуре также соответствует двойственная фигура. Примеры: 1. фигуре «прямая и три точки на ней» соответствует фигура «точка и три прямые, проходящие через нее»;
ей фигура «три прямые, не проходящие через одну точку, и три точки их пересечения» (она называется трехсторонником). Ясно, что это одна и та же фигура. Замечание. В проективном пространстве выполняется аналогичный принцип – «большой принцип двойственности». В любом утверждении относительно точек, прямых и плоскостей в проективном пространстве можно слово «плоскость» заменить на слово «точка», и наоборот. Утверждение останется истинным (принцип двойственности на плоскости называется малым).
25 Проективные координаты на проективной прямой. Опр. 2.1.1. Проективной системой координат (проективным репером) на проективной прямой наз. Произв-ая упорядоченная тройка точек этой прямой.
Пусть O Ï – произвольная точка, а – плоскость, которая проходит через O и. Будем все векторы в плоскости a, откладывать из точки O. Опр. 2.1.2. Говорим, что векторпорождает точку M на прямой, если лежит на прямой OM. Будем обозначать так: M , или p( ) = M. Очевидно, что
"lÎ R \{0} p( ) = p(l ). (2.1) Опр. 2.1.3. Говорим, что базис B = {, } в плоскости порождает репер R = { A 1, A 2, E }, если p( ) = A 1 , p( ) = A 2 , p( + ) = E. Пишем: p(B ) = R. Теорема 2.1.1. Для любого репера R на прямой существует единственный с точностью до гомотетии с центром O базис B, который порождает репер R.
Опр. 2.1.4. Пусть базис B порождает репер R, а вектор – точку M. Проективными координатами точки M на прямойв репере R наз.координаты вектора относительно базиса B. Из (2.1) и т 2.1.1вытекает, что эти координаты определяются с точностью до пропорциональности, т.е. данная точка в данном репере имеет не одну пару корд. (x 1, x 2), а мн-во пар, пропорц-ных друг другу. Поэтому зап-ют так: M (x 1: x 2). Чтобы найти координаты (x 1, x 2) точки M Î в репере R, необходимо: 1. выбрать собственную точку O Ï; 2. выбрать базис B, который порождает R; 3. выбрать вектор на прямой OM; 4. найти корд-ты (x 1, x 2) этого вектора в базисе B (они и будут проективными корд-ми точки M, т.е. M (x 1: x 2)). В частности, поскольку p( ) = A 1 , p( ) = A 2 , p( + ) = E, то A 1(1,0), A 2(0,1), E (1,1). Теперь понятно, почему точка E называется единичной. Замечание. Позже будет показано, что координаты точки M в репере R не зависят от выбора точки O. Заметим также, что для любой точки M (x 1: x 2) числа x 1, x 2 не равны нулю одновременно: x 12 + x 22 ¹ 0. Очень простой смысл имеют проективные координаты в репере, первая точка которого несобственная. Пусть R = { A 1¥, A 2, E } – такой репер
=, =, =, =. Тогда ½½, т.е. $ x Î R: = x. Поэтому = + = x +. Значит, проективные координаты x 1: x 2 точки M в таком репере будут x:1, где x – обычная координата точки M в аффинной системе координат на прямой с началом A 2 и единичной точкой E. На рисунке M (3:1). Опр. 2.1.5. Проективные координаты в репере, одна точка которого несобственная, называются однородными аффинными координатами на прямой.
26. Однородные аффинные координаты на плоскости.
Таким образом, каждая точка M Îa имеет две координаты (x, y). На проективной плоскости этих координат не хватает (для несобственных точек). Опр. 2.2.1. Однородными аффинными координатами собственной точки M (x, y) называются числа x 1, x 2, x 3 такие, что x = x 1/ x 3 , y = x 2 / x 3 , или, что то же самое, x 1: x 2 : x 3 = x : y : 1. Очевидно, что такие координаты определяются с точностью до пропорциональности. Рассмотрим несобственную точку M ¥. Она определяется прямой l. Пусть ее уравнение в аффинной системе координат ax + by + c = 0. Пусть M (x, y) – произвольная собственная точка прямой. Тогда y = – (ax + с) / b, т.е. M (x, – (ax + с) / b). Значит, однородные координаты точки M будут (x, – (ax + с) / b, 1) или (b, – a – с / x, b / x). Несобственную точку прямой можно рассматривать, как предел собственной точки, когда она бесконечно удаляется по прямой. Поэтому однородные координаты M ¥получаем, как предел (b, – a – с / x, b / x) = (b, – a , 0) Û M ¥(b: – a: 0). Для решения многих задач удобнее пользоваться другими координатами.
27. Проективные координаты на проективной плоскости. Опр. 2.3.1. Проективной системой координат (проективным репером) на проективной плоскости наз.произвольная упорядоченная четверка точек этой плоскости R = { A 1, A 2, A 3, E }, никакие три из которых не лежат на одной прямой. Точки A 1, A 2, A 3 называются вершинами репера, а E – единичной точкой. Выберем произвольную собственную точку O Ï и будем откладывать от нее все векторы. Опр. 2.3.2. Говорим, что векторпорождает точку M Î, если лежит на прямой OM. Пишем p( ) = M. Очевидно, что "lÎ R \{0} p( ) = p(l ). Опр. 2.3.3. Говорим, что базис B = {, , } в пространстве порождает репер R = { A 1, A 2, A 3, E }, если p( ) = A 1 , p( ) = A 2 , p( ) = A 3, p( + + ) = E. Пишем: p(B ) = R.
Д-во аналогично доказательству теоремы 2.1.1. Опр. 2.3.4. Пусть базис B порождает репер R, а вектор – точку M. Проективными координатами точки M Î в репере R называются координаты вектора относительно базиса B. Очевидно, что проективные координаты определяются с точностью до пропорциональности. Поэтому их часто записывают так: M (x 1: x 2: x 3). В частности, A 1(1, 0, 0), A 2(0,1, 0), A 3(0, 0, 1), E (1, 1, 1). Позже мы докажем, что проективные координаты точки на не зависят от выбора точки O.
Пусть R = { A 1, A 2, A 3, E } –произвольный проективный репер на плоскости. Спроецируем E из вершины A 1 на прямую A 2 A 3; получим точку E 1. Проецируя E из A 2 на A 1 A 3, получим E 2 , а проецируя E из A 3 на A 1 A 2, получим E 3. На прямых A 2 A 3, A 1 A 3, A 1 A 2 получились проективные реперы R 1={ A 2, A 3, E 1}, R 2= { A 1, A 3, E 2}, R 3= { A 1, A 2, E 3}. Пусть M Î – произвольная точка.Аналогичным образом пол-ем точки M 1, M 2, M 3. Теорема 2.4.1. M (x 1, x 2, x 3) R Û { M 1(x 2, x 3) R 1 & M 2(x 1, x 3) R 2 & & M 3(x 1, x 2) R 3}. Эта теорема позволяет: 1. находить проективные координаты точки на плоскости; 2. строить точку по ее координатам, не выходя за пределы плоскости. Для решения первой задачи а) строим точки E 1, M 1, E 2, M 2; б) находим координаты x 1, x 2 точки M 1в репере R 1={ A 2, A 3, E 1}; в) находим координаты x ¢1, x ¢3 точки M 2в репере R 2= { A 1, A 3, E 2}; г) координаты x ¢1 , x ¢3 заменяем пропорционально на x 1, x 3: (x 1: x 3 = x ¢1 : x ¢3). д) M (x 1, x 2, x 3) R. Задача 2 решается аналогично. Пример. В репере R = { A 1, A 2, A 3, E } построить точку M (3:2:1). Построение. 1) Выбираем репер R = { A 1, A 2, A 3, E }; 2) строим реперы R 1={ A 2, A 3, E 1} и R 2= { A 1, A 3, E 2} (см. рисунок); 3) в репере R 1 строим точк M 1(2:1); для этого
а) выбираем точку O 1Ï A 2 A 3 и проводим прямые O 1 A 2 , O 1 A 3 , O 1 E 1 ; б)на прям. O 1 E 1 откл-ем вектор от точки O 1; в) раскладываем на составляющие, параллельные O 1 A 2 и O 1 A 3 : = + и получаем базис {, }; г) в этом базисе строим вектор (2, 1) (т.е. = 2 + ), отложенный от точки O 1; д) проводим прямую l 1½½ через точку O 1; тогда M 1= l 1 I A 2 A 3 ; 4) в репере R 2= { A 1, A 3, E 2} аналогично пункту 3) строим точку M 2(3:1); 5) M = A 1 M 1I A 2 M 2 – искомая точка.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 669; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.78.249 (0.014 с.) |

 1. Через две различные точки проходит, и притом, единственная прямая.
1. Через две различные точки проходит, и притом, единственная прямая. 2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, которая проходит через эту точку.
2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, которая проходит через эту точку.
 3. Если две различные прямые имеют общую тчк, то через них можно провести плоск, и при этом, только одну.
3. Если две различные прямые имеют общую тчк, то через них можно провести плоск, и при этом, только одну. 4. Через прямую и не лежащую на ней точку можно провести плоскость, и притом, только одну.
4. Через прямую и не лежащую на ней точку можно провести плоскость, и притом, только одну.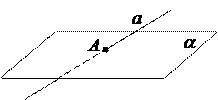 9. Любые две различные плоскости имеют общую прямую и, притом, только одну.
9. Любые две различные плоскости имеют общую прямую и, притом, только одну. Для д-ва, напр., св-ва 8 необходимо расс-ть след-ие возможные случаи:
Для д-ва, напр., св-ва 8 необходимо расс-ть след-ие возможные случаи:
 а) плоскость и прямая собственные, и прямая не параллельна плоскости; тогда имеем обычную точку пересечения.
а) плоскость и прямая собственные, и прямая не параллельна плоскости; тогда имеем обычную точку пересечения.
 б) плоскость и прямая собственные, и прямая параллельна плоскости;
б) плоскость и прямая собственные, и прямая параллельна плоскости;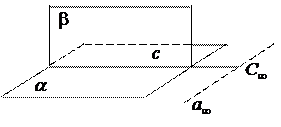
 г) плоскость b собственная, а прямая a ¥ несобственная; тогда a ¥ задается плоскостью a и общей точкой a ¥ и b будет несобственная точка C ¥ прямой c = b I a.
г) плоскость b собственная, а прямая a ¥ несобственная; тогда a ¥ задается плоскостью a и общей точкой a ¥ и b будет несобственная точка C ¥ прямой c = b I a. 2. фигуре «три точки, не лежащие на одной прямой, и три прямые, которые проходят через эти точки» (она называется трехвершинником) соответствует двойственная
2. фигуре «три точки, не лежащие на одной прямой, и три прямые, которые проходят через эти точки» (она называется трехвершинником) соответствует двойственная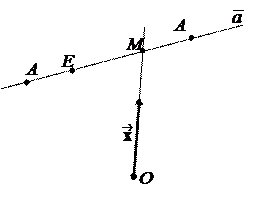 Проективный репер обычно обозначается буквой R, а точки, из которых он состоит – A 1, A 2 , E . Причем E называется единичной точкой репера. В дальнейшем проективный репер часто будем называть просто репером.
Проективный репер обычно обозначается буквой R, а точки, из которых он состоит – A 1, A 2 , E . Причем E называется единичной точкой репера. В дальнейшем проективный репер часто будем называть просто репером. Пусть R = { A 1, A 2, E } – репер на, O Ï. Возьмем произвольный вектор на прямой OE и разложим его на составляющие, лежащие на прямых OA 1 и OA 2: = + . Базис B = {, } – искомый. Очевидно, подойдет и базис {l,l}, l ¹ 0.
Пусть R = { A 1, A 2, E } – репер на, O Ï. Возьмем произвольный вектор на прямой OE и разложим его на составляющие, лежащие на прямых OA 1 и OA 2: = + . Базис B = {, } – искомый. Очевидно, подойдет и базис {l,l}, l ¹ 0.  и M – произвольная собственная точка на прямой. Тогда прямая OA 1¥½½. Обозначим
и M – произвольная собственная точка на прямой. Тогда прямая OA 1¥½½. Обозначим Как известно, аффинная система координат на обычной плоскости a определяется началом O и векторным базисом B = {, }. Аффинные координаты произвольной точки M Îa совпадают с координатами ее радиус-вектора, т.е. они равны коэффициентам разложения = x + y.
Как известно, аффинная система координат на обычной плоскости a определяется началом O и векторным базисом B = {, }. Аффинные координаты произвольной точки M Îa совпадают с координатами ее радиус-вектора, т.е. они равны коэффициентам разложения = x + y. Теорем 2.3.1. Для любого репера R на плоскости сущ-ет единственный с точностью до гомотетии с центром O базис B, который порождает репер R.
Теорем 2.3.1. Для любого репера R на плоскости сущ-ет единственный с точностью до гомотетии с центром O базис B, который порождает репер R. 28Связь между проективными координатами на плоск. и на прям.
28Связь между проективными координатами на плоск. и на прям.


