Построение линии пересечения поверхности проецирующими плоскостями

 

Для решения этой задачи необходимо понимать, что линия пересечения поверхности с плоскостью есть множество точек, принадлежащих одновременно и поверхности и плоскости, а, следовательно, эта линия есть плоская кривая, все точки которой принадлежат поверхности.

В случае если плоскость проецирующая, линия пересечения совпадает с прямой, в которую проецируется плоскость, и находится в пределах очерка поверхности. Следовательно, одна проекция линии пересечения поверхности с плоскостью известна. Для нахождения второй проекции линии пересечения поверхности с плоскостью используется условие принадлежности точек этой линии поверхности, т.е. решается задача по нахождению недостающей проекции точки, лежащей на поверхности.

 

 

Сечение призмы проецирующей плоскостью

 

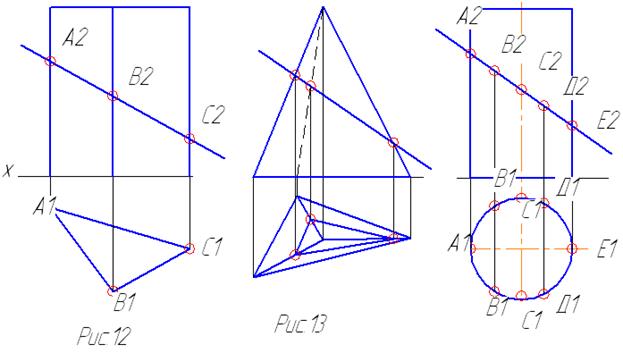
Если призма прямая, т.е. ребра призмы перпендикулярны плоскости проекций, то проекции линии пересечения определены сразу, т.к. одна проекция совпадает с проекцией плоскости, а вторая - совпадает с основанием призмы (рис.12).

 

Сечение пирамиды проецирующей плоскостью

 

Дана пирамида, в основании которой лежит треугольник. Эта пирамида пересекается с проецирующей плоскостью. Одна проекция линии пересечения известна - она совпадает с прямой, в которую проецируется плоскость. В сечении получается треугольник, вершины которого лежат на ребрах пирамиды, а, следовательно, найти недостающие проекции вершин просто, как точки, лежащие на прямой (рис.13).

 

 

Сечение цилиндра проецирующей плоскостью

 

Дан прямой цилиндр, он пересекается с проецирующей плоскостью. Цилиндр- это поверхность, которая на одну из плоскостей проекций проецируется в окружность, т.е. в линию. Это обстоятельство упрощает решение, т.к. любая точка, лежащая на поверхности цилиндра, проецируется на окружность, а, следовательно, проекции линии пересечения цилиндра с плоскостью известны сразу - одна проекция совпадает с проекцией плоскости, а вторая- с окружностью, в которую проецируется цилиндр (рис. 14).

 

 

Рис.14

 

 

Сечение конуса проецирующей плоскостью

 

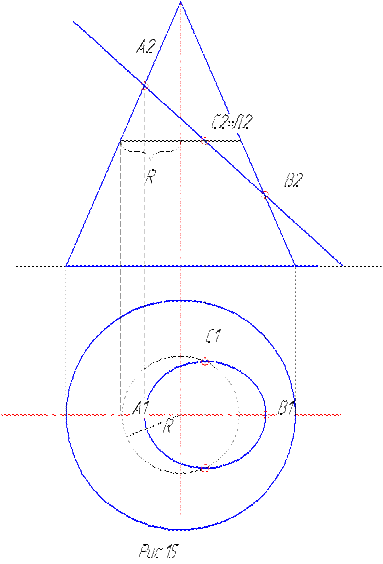
Дан прямой круговой конус, т.е. конус, у которого ось вращения перпендикулярна основанию. Конус пересекается с проецирующей плоскостью. Одна проекция линии пересечения совпадает с проекцией прямой, в которую проецируется плоскость. Вторую проекцию линии пересечения ищем из условия принадлежности точек конусу.

Если точка принадлежит конусу, то через неё можно провести линию, лежащую на конусе. Самая простая линия, принадлежащая конусу - это окружность, лежащая в плоскости, перпендикулярной оси конуса. Следовательно, чтобы найти точку на конусе, надо:

1. через известную проекцию точки провести поперечное сечение конуса плоскостью. В сечении получится окружность, радиус которой известен - расстояние от оси конуса до очерковой образующей,

2.на горизонтальной проекции конуса построить окружность данного радиуса и по линии связи найти, недостающую проекцию точки (рис. 15).

 

 

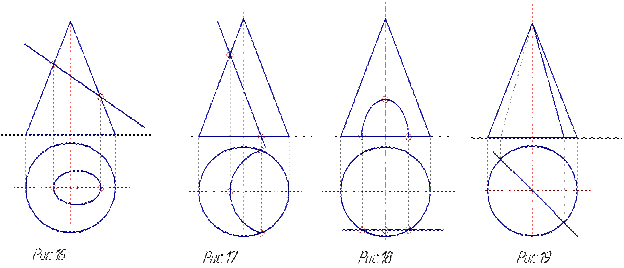
В зависимости от того, как проходит плоскость по конусу, в сечении будет получаться:

1) эллипс- рис. 16, 2) парабола- рис. 17, 3) гипербола- рис. 18, 4) треугольник- рис. 19.

 

 

 

Сечение сферы проецирующей плоскостью

 

Дана сфера, которую пересекает проецирующая плоскость. Одна проекция линии пересечения известна - она совпадает с прямой, в которую проецируется плоскость. Вторую проекцию линии находят из условия принадлежности её точек сфере.

Сфера- это особая поверхность, в любом сечении которой лежит окружность. Правда в зависимости от её расположения по отношению к плоскостям проекций она может проецироваться и в окружность, и в эллипс. Поэтому, для нахождения точки на поверхности сферы используем поперечное сечение сферы, которое параллельно одной из плоскостей проекций. Радиус сечения равен расстоянию от оси сферы до очерка. Нахождение недостающей проекции точки проводят аналогично нахождению точки на конусе (рис. 20).