По выполнению заданий № 3 и 4

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

РОССИИ

ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

МИАССКИЙ ФИЛИАЛ

МАШИНОСТРОИТЕЛЬНЫЙ ФИЛИАЛ

 

 

БЕРЕЖКО Л.Н.

 

 

МЕТОДИЧЕСКОЕ ПОСОБИЕ

для студентов очной формы обучения

По выполнению заданий № 3 и 4

ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

Тема «Поверхности»

 

 

Миасс,2007

 

СОДЕРЖАНИЕ

 

СОДЕРЖАНИЕ.. 2

ВВЕДЕНИЕ.. 3

1.РЕШЕНИЕ ЗАДАНИЯ №3. 4

1.1 Метод замены плоскостей проекций. 4

1.2. Преобразование плоскости общего положения в проецирующую плоскость. 6

1.3. Преобразование поверхности. 7

1.4. Построение линии пересечения поверхности проецирующими плоскостями. 10

1.4.1.Сечение призмы проецирующей плоскостью.. 11

1.4.2.Сечение пирамиды проецирующей плоскостью.. 11

1.4.3. Сечение цилиндра проецирующей плоскостью.. 11

1.4.4. Сечение конуса проецирующей плоскостью.. 12

1.4.5. Сечение сферы проецирующей плоскостью.. 14

1.5. Построение линии пересечения геометрического тела плоскостью.. 15

1.6. Построение натурального вида сечения. 16

2. РЕШЕНИЕ ЗАДАДАНИЯ № 4. 18

2.1. Пересечение поверхностей. 18

2.1.1. Пересечение поверхностей, одна из которых занимает простейшее положение. 19

2.1.2.Метод вспомогательных секущих плоскостей. 20

2.1.3. Метод вспомогательных концентрических сфер. 23

2.1.4. Заключение по первой части задания №4. 26

2.2. Построение разверток поверхностей. 27

2.2.1. Развертка призмы.. 27

2.2.2. Развертка пирамиды.. 28

2.2.3. Развертка цилиндра. 32

2.2.4. Развертка конуса. 33

ЗАКЛЮЧЕНИЕ.. 35

 

 

ВВЕДЕНИЕ

 

 

Контрольные задания № 3и4 по начертательной геометрии выполняются студентами после изучения следующих тем:

1.Методы преобразования проекций. Замена плоскостей проекций.

2.Сечение поверхности проецирующими плоскостями.

3.Взаимное пересечение поверхностей.

Изучение этих тем позволит выполнить контрольные задания без особых усилий, так как в основе решения задач лежит материал, изложенный в этих темах. Кроме того, желательно ознакомиться с методическими указаниями по решению метрических задач методом замены плоскостей проекций, имеющихся на кафедре технической механики.

В данном методическом пособии рассмотрен порядок выполнения контрольных заданий с изложением основного теоретического материала, знание которого необходимо для решения задач.

 

РЕШЕНИЕ ЗАДАНИЯ №3

 

Условие задачи сформулировано следующим образом.

Даны: непрозрачное геометрическое тело и секущая плоскость, заданная двумя пересекающимися прямыми.

Требуется на комплексном чертеже:

1.Построить проекции линии пересечения поверхности геометрического тела плоскостью.

2.Определить видимость элементов геометрического тела и линии сечения.

3.Построить истинный вид сечения.

Варианты задач представлены в методических указаниях.

Геометрическое тело представляет собой совокупность нескольких поверхностей, например, цилиндр и конус или призма, в основании которой лежит правильный пятиугольник, и конус, который стоит на этой призме.

Секущая плоскость задана двумя пересекающимися прямыми и является плоскостью общего положения. Решение задачи сводится к построению линии пересечения этих поверхностей плоскостью общего положения. В общем виде построение линии пересечения поверхности плоскостью общего положения решается довольно сложно. Особенно это касается таких поверхностей как пирамида, конус и сфера.

Но если плоскость занимает проецирующее положение, то решение задачи по построению линии пересечения поверхности такой плоскостью значительно упрощается.

Следовательно, решение задачи удобно проводить после преобразования плоскости общего положения в проецирующую, т.е. перпендикулярную одной из плоскостей проекций. Это преобразование проведем с помощью метода замены плоскостей проекций.

Разберем основы этого метода в следующем подразделе.

 

Построение линии пересечения поверхности проецирующими плоскостями

 

Для решения этой задачи необходимо понимать, что линия пересечения поверхности с плоскостью есть множество точек, принадлежащих одновременно и поверхности и плоскости, а, следовательно, эта линия есть плоская кривая, все точки которой принадлежат поверхности.

В случае если плоскость проецирующая, линия пересечения совпадает с прямой, в которую проецируется плоскость, и находится в пределах очерка поверхности. Следовательно, одна проекция линии пересечения поверхности с плоскостью известна. Для нахождения второй проекции линии пересечения поверхности с плоскостью используется условие принадлежности точек этой линии поверхности, т.е. решается задача по нахождению недостающей проекции точки, лежащей на поверхности.

 

 

Сечение призмы проецирующей плоскостью

 

Если призма прямая, т.е. ребра призмы перпендикулярны плоскости проекций, то проекции линии пересечения определены сразу, т.к. одна проекция совпадает с проекцией плоскости, а вторая - совпадает с основанием призмы (рис.12).

 

Сечение пирамиды проецирующей плоскостью

 

Дана пирамида, в основании которой лежит треугольник. Эта пирамида пересекается с проецирующей плоскостью. Одна проекция линии пересечения известна - она совпадает с прямой, в которую проецируется плоскость. В сечении получается треугольник, вершины которого лежат на ребрах пирамиды, а, следовательно, найти недостающие проекции вершин просто, как точки, лежащие на прямой (рис.13).

 

 

РЕШЕНИЕ ЗАДАДАНИЯ № 4

 

Условие задания сформулировано следующим образом:

 

Построить проекции линии пересечения двух поверхностей. Выполнить развертку одной из поверхностей, на которой найти все точки линии пересечения.

 

Пересечение поверхностей

 

Пересечение двух поверхностей между собой происходит по линии, которую называют линией пересечения. Множество точек, образующих эту линию, принадлежат одновременно обеим пересекающимся поверхностям.

 

Вид или форма этой линии зависит от того, какого вида поверхности пересекаются между собой:

1) если пересекаются гранные поверхности (пирамиды и призмы), то линия пересечения есть ломаная пространственная, состоящая из отрезков прямых,

2) если пересекаются гранная поверхность с поверхностью вращения (цилиндр с призмой), то линия пересечения есть пространственная, состоящая из плоских кривых,

3) если пересекаются две поверхности вращения (конус с цилиндром), то линия пересечения есть пространственная кривая линия.

При построении линии пересечения поверхностей надо искать точки общие у поверхностей. Существует множество способов отыскания таких точек.

Рассмотрим основные из них:

1) простейшее расположение одной из поверхностей,

2) метод вспомогательных секущих плоскостей,

3) метод вспомогательных секущих концентрических сфер.

 

 

Построение разверток поверхностей

 

Вторая часть задачи №2 состоит из построения развертки одной из пересекающихся поверхностей с нанесением на ней точек линии пересечения. Выбор развертываемой поверхности зависит от желания студента. Но необходимо учесть, что не стоит разворачивать сферу или тор. Лучше развернуть гранную поверхность или цилиндр, или конус.

 

 

Развертка призмы

 

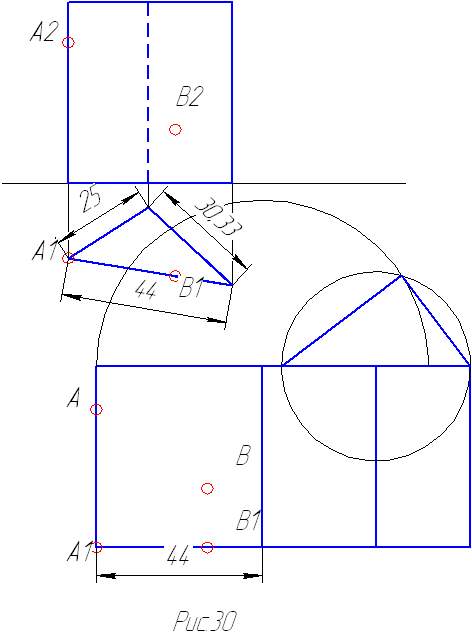
Развертка призмы представляет собой прямоугольник, высота которого равна высоте призмы, а длина равна периметру основания призмы. Если призма прямая, то построение развертки выполняется просто, т.к. на чертеже есть натуральная величина и основания призмы и ее высота (рис.30).

 

 

 

 

Развертка пирамиды

 

 

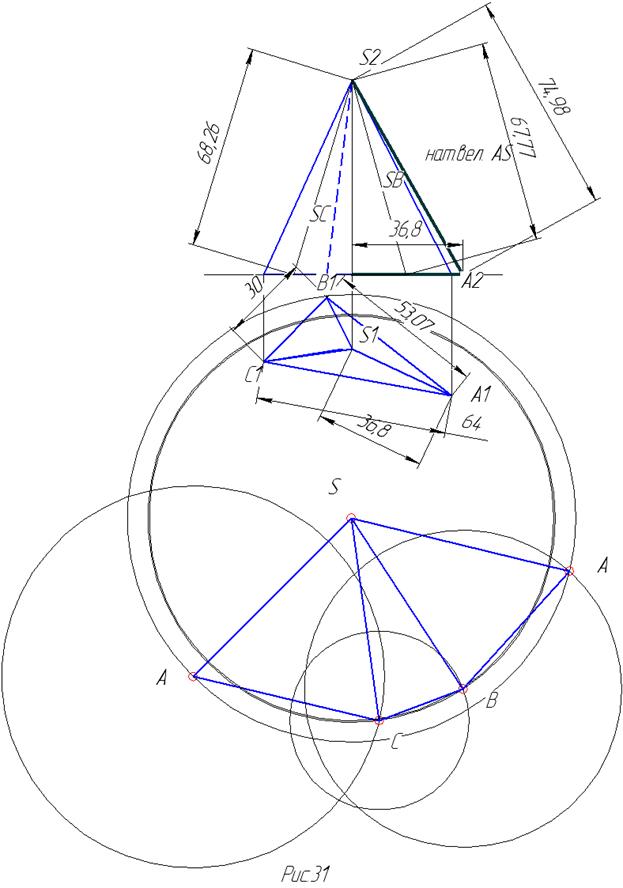
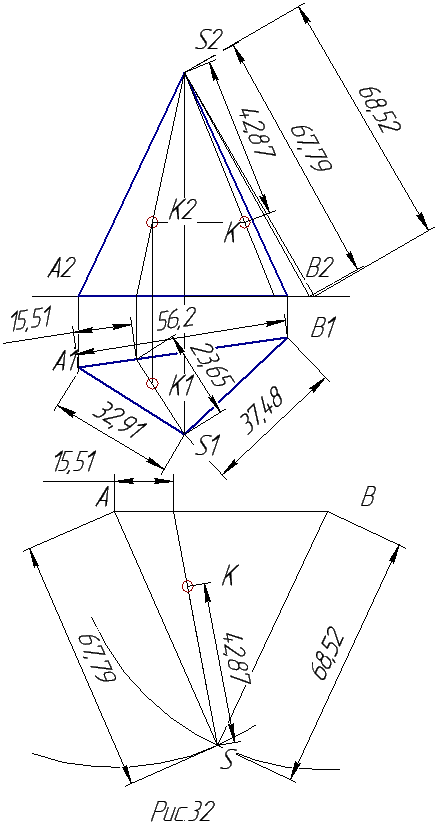
Чертеж пирамиды и построение ее развертки показаны на рисунке 31. Из чертежа видно, что натуральная величина основания пирамиды совпадает с горизонтальной проекцией основания пирамиды, а вот ребра пирамиды не проецируются на плоскости проекций в натуральную величину. Следовательно, для построения развертки надо построить сначала натуральную величину ребер пирамиды. Можно воспользоваться нахождением натуральной величины отрезка с помощью прямоугольного треугольника. Причем если рассматривать ребра пирамиды как отрезки, то для всех ребер пирамиды разница координат Z одинакова и равна высоте пирамиды. Поэтому, чтобы найти величину ребра пирамиды, достаточно отложить величину горизонтальной проекции ребра по оси Х, используя высоту пирамиды как катет прямоугольного треугольника, тогда гипотенуза этого треугольника и есть натуральная величина ребра.

Развертка пирамиды есть треугольники, являющиеся натуральной величиной боковых граней пирамиды и ее основания (рис.31).

Точку на поверхности пирамиды надо искать из условия принадлежности точки плоскости. Следовательно, через точку надо провести прямую, лежащую в плоскости треугольника, построить ее на развертке и на ней найти саму точку (рис.32).Причем прямую надо проводить так, чтобы ее можно было просто построить на развертке, например, через вершину треугольника на основание.

 

 

 

.

 

Развертка цилиндра

 

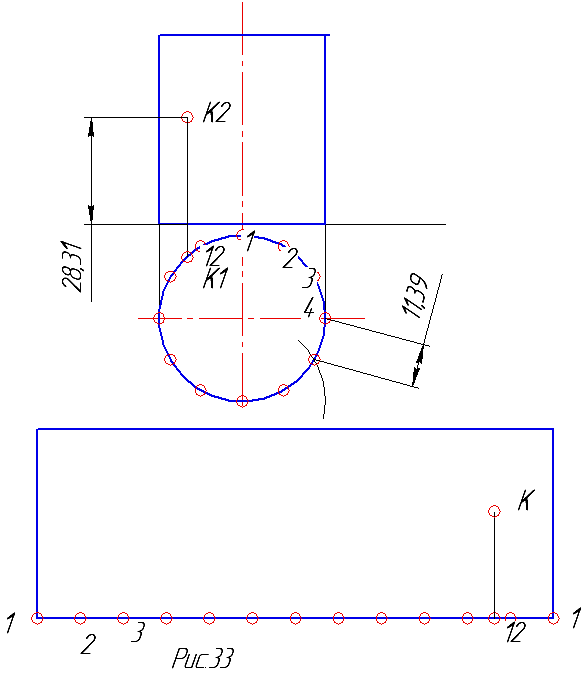
Развертка боковой поверхности цилиндра есть прямоугольник, высота которого есть высота цилиндра, а длина равна длине окружности основания цилиндра. Для того чтобы не считать длину окружности основания цилиндра и для упрощения нахождения в дальнейшем точек на поверхности, применим метод разбивки основания цилиндра на равное количество частей и чем больше это количество, тем точнее будет построение, т.к. длину дуги будем заменять длиной хорды, соединяющей концы дуги (рис.33).

 

 

Развертка конуса

 

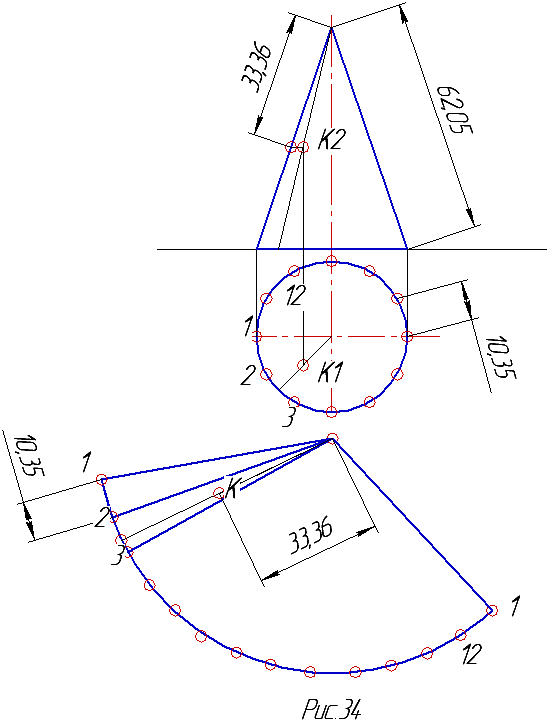
Развертка боковой поверхности конуса есть сектор круга, радиус которого равен натуральной величине образующей конуса. Угол этого конуса можно рассчитать по формуле, но это непрактично, т.к. при построении развертки подразумевается то, что надо будет искать точки на поверхности. Поэтому в качестве ограничения сектора лучше использовать крайние точки, лежащие на основании сектора, т.е. на дуге. Для этого надо разбить основание конуса на равные части аналогично построению развертки цилиндра и, заменяя длину дуги длиной хорды, отложить необходимое количество отрезков по дуге, радиус которой равен длине образующей конуса (рис.34). На этом же рисунке показано нахождение точки на поверхности конуса. Для нахождения точки надо через нее провести образующую. Найти основание образующей, найти на развертке это основание, через него провести образующую на развертке и на ней отложить расстояние от точки до вершины конуса. Причем это расстояние находят на чертеже. Для этого фронтальную проекцию точки переносят на очерковую образующую с помощью горизонтальной линии и тогда расстояние от точки до вершины конуса замеряют по очерковой образующей.

 

 

ЗАКЛЮЧЕНИЕ

 

В данном методическом пособии рассмотрены приемы решения задач по теме поверхности. Решение необходимо проводить сначала на черновике большого формата для выяснения того, как лучше расположить чертеж в чистовом варианте. Желательно, прежде чем оформлять решение, показать черновик преподавателю и только после этого проводить оформление.

 

 

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

РОССИИ

ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

МИАССКИЙ ФИЛИАЛ

МАШИНОСТРОИТЕЛЬНЫЙ ФИЛИАЛ

 

 

БЕРЕЖКО Л.Н.

 

 

МЕТОДИЧЕСКОЕ ПОСОБИЕ

для студентов очной формы обучения

по выполнению заданий № 3 и 4

ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

Тема «Поверхности»

 

 

Миасс,2007

 

СОДЕРЖАНИЕ

 

СОДЕРЖАНИЕ.. 2

ВВЕДЕНИЕ.. 3

1.РЕШЕНИЕ ЗАДАНИЯ №3. 4

1.1 Метод замены плоскостей проекций. 4

1.2. Преобразование плоскости общего положения в проецирующую плоскость. 6

1.3. Преобразование поверхности. 7

1.4. Построение линии пересечения поверхности проецирующими плоскостями. 10

1.4.1.Сечение призмы проецирующей плоскостью.. 11

1.4.2.Сечение пирамиды проецирующей плоскостью.. 11

1.4.3. Сечение цилиндра проецирующей плоскостью.. 11

1.4.4. Сечение конуса проецирующей плоскостью.. 12

1.4.5. Сечение сферы проецирующей плоскостью.. 14

1.5. Построение линии пересечения геометрического тела плоскостью.. 15

1.6. Построение натурального вида сечения. 16

2. РЕШЕНИЕ ЗАДАДАНИЯ № 4. 18

2.1. Пересечение поверхностей. 18

2.1.1. Пересечение поверхностей, одна из которых занимает простейшее положение. 19

2.1.2.Метод вспомогательных секущих плоскостей. 20

2.1.3. Метод вспомогательных концентрических сфер. 23

2.1.4. Заключение по первой части задания №4. 26

2.2. Построение разверток поверхностей. 27

2.2.1. Развертка призмы.. 27

2.2.2. Развертка пирамиды.. 28

2.2.3. Развертка цилиндра. 32

2.2.4. Развертка конуса. 33

ЗАКЛЮЧЕНИЕ.. 35

 

 

ВВЕДЕНИЕ

 

 

Контрольные задания № 3и4 по начертательной геометрии выполняются студентами после изучения следующих тем:

1.Методы преобразования проекций. Замена плоскостей проекций.

2.Сечение поверхности проецирующими плоскостями.

3.Взаимное пересечение поверхностей.

Изучение этих тем позволит выполнить контрольные задания без особых усилий, так как в основе решения задач лежит материал, изложенный в этих темах. Кроме того, желательно ознакомиться с методическими указаниями по решению метрических задач методом замены плоскостей проекций, имеющихся на кафедре технической механики.

В данном методическом пособии рассмотрен порядок выполнения контрольных заданий с изложением основного теоретического материала, знание которого необходимо для решения задач.

 

РЕШЕНИЕ ЗАДАНИЯ №3

 

Условие задачи сформулировано следующим образом.

Даны: непрозрачное геометрическое тело и секущая плоскость, заданная двумя пересекающимися прямыми.

Требуется на комплексном чертеже:

1.Построить проекции линии пересечения поверхности геометрического тела плоскостью.

2.Определить видимость элементов геометрического тела и линии сечения.

3.Построить истинный вид сечения.

Варианты задач представлены в методических указаниях.

Геометрическое тело представляет собой совокупность нескольких поверхностей, например, цилиндр и конус или призма, в основании которой лежит правильный пятиугольник, и конус, который стоит на этой призме.

Секущая плоскость задана двумя пересекающимися прямыми и является плоскостью общего положения. Решение задачи сводится к построению линии пересечения этих поверхностей плоскостью общего положения. В общем виде построение линии пересечения поверхности плоскостью общего положения решается довольно сложно. Особенно это касается таких поверхностей как пирамида, конус и сфера.

Но если плоскость занимает проецирующее положение, то решение задачи по построению линии пересечения поверхности такой плоскостью значительно упрощается.

Следовательно, решение задачи удобно проводить после преобразования плоскости общего положения в проецирующую, т.е. перпендикулярную одной из плоскостей проекций. Это преобразование проведем с помощью метода замены плоскостей проекций.

Разберем основы этого метода в следующем подразделе.