
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистика регистрации ядерного излученияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача 2.34
Решение Используя биномиальный закон (2.5) и формулы (2.6) и (2.7), получим
Задача 2.35
Решение Ожидаемое число измерений, в которых может быть зафиксировано точно ni импульсов будет равно N (ni) = N · P (ni), где P (ni) - вероятность появления точно ni импульсов, число которых пропорционально количеству распадающихся ядер за этот же промежуток времени. Эта вероятность определяется с помощью биномиального закона распределения вероятностей (2.5), если известно полное число возможных событий N 0 и время t каждого измерения. Но величины N 0 и t неизвестны, и использовать формулу (2.5) не представляется возможным. Однако в случае n << N 0 и t << T 1/2 биномиальный закон распределения вероятностей (2.5) может быть представлен в виде распределения Пуассона (2.8). Тогда N (ni) = N и N (n1) = 2000 N (n2) = 2000 Задача 2.36
Решение Согласно условию задачи предполагаем, что время проведения измерений существенно меньше периода полураспада исследуемого радионуклида и для вычисления искомых вероятностей можно воспользоваться распределением Пуассона (2.8). Однако использование формулы (2.8) технически затруднительно, так как связано с вычислением факториалов больших чисел и возведением чисел в степени с большими показателями. Получить более удобную для вычислений форму можно, если воспользоваться утверждением центральной предельной теоремы (ЦПТ) теории вероятности, согласно которой при μ >> 1 распределение Пуассона переходит в нормальное распределение с дисперсией, равной μ:
Тогда
Очевидно, что сумма вероятностей появления любого значения скорости счета импульсов от
Используя формулу (2.36.1), вычислим
Таким образом,
Вычислить вероятность получения абсолютной погрешности измерения, превосходящей: а) σ и б) 2σ, где σ – среднеквадратичная погрешность. Решение Предполагаем, что случайная величина имеет нормальный закон распределения. Тогда искомая вероятность будет равна
Если в интеграле произвести замены:
то получим
где Ф(α) – интеграл ошибок, который не выражается в элементарных функциях и значения которого можно найти в подробных таблицах. Для поставленной задачи α =1 и α = 2 и соответственно: Ф(1) = 0,683; Ф(2) = 0,955. Задача 2.38
Решение По определению средняя скорость счета
Погрешность измерения числа импульсов является принципиально неустранимой, так как вызвана статистическим характером распада большого числа радиоактивных ядер. Измерение же времени обычно выполняется с относительной погрешностью, существенно меньшей, чем при измерении числа импульсов, и потому ее величиной можно пренебречь. Тогда, если предположить, что условия применения распределения Пуассона выполнены, можно воспользоваться формулой (2.10) и
Относительная погрешность измерения числа импульсов
Следует отметить, что эта погрешность соответствует доверительной вероятности 68%. Если использовать значение доверительной вероятности 95%, как принято в настоящее время, то полученную величину надо удвоить (см. предыдущую задачу):
Тогда число импульсов, которое необходимо зарегистрировать для получения заданной относительной точности с доверительной вероятностью 95%, составит
Необходимое время измерений составит
Задача 2.39
Решение Фоном принято называть излучение, не связанное с исследуемым излучением, действие которого на счетчик не представляется возможным исключить. Поэтому
Средняя квадратичная погрешность искомой скорости счета будет равна, согласно (2.9) и (2.12):
Скорость счета импульсов от фона составляет 15 имп./мин, а скорость счета от исследуемого препарата и фона составляет 60 имп./мин. Пусть t ф и t иф – время измерения фона и исследуемого препарата при наличии фона. Найти оптимальное отношение t ф/ t иф, при котором точность определения скорости счета от самого препарата будет максимальной для заданного полного времени t ф + t иф. Решение
Для нахождения отношения t ф/ t иф, которое отвечает минимальному значению σи, вычислим полный дифференциал от (2.40.1) и приравняем его к нулю. Имеем
Из условия
Подставив (2.30.3) в (2.40.2), получим
Задача 2.41
Решение
Пусть время измерения t >> τ. Тогда среднее число частиц N 0, прошедших через счетчик за это время, можно представит следующим образом:
где N >> 1 – число частиц, зарегистрированных за время t; Δ N =
так как τ N – суммарное время, в течение которого счетчик не мог регистрировать частицы. Тогда
Разделив левую и правую части уравнения (2.41.3) на t, получим
Из последнего уравнения
Задача 2.42
Решение Количество просчитанных импульсов (используем формулу (2.41.3) из предыдущей задачи) равно
Тогда η1 = 100·1,0·10-6= 10-4 = 0,01% η2 = 105·1,0·10-6 = 0,1 = 10%
Задачи для самостоятельного решения
2.43. Какая доля первоначального количества ядер радиоактивного препарата со средним временем жизни τ: а) останется через интервал времени, равный 10 τ? б) распадется за интервал времени между t 1= τ и t 2=2 τ? 2.44. Какая доля радиоактивного нуклида 32Р распадется в течение второй недели (за вторую неделю) с момента приготовления препарата. 2.45. Определить вероятность распада ядра радиоактивного ядра золота 198Au: а) за четверо суток; б) за четвертые сутки. 2.46. Во сколько раз вероятность распада ядер радиоактивного 128I в течение первых суток, больше вероятности распада за вторые сутки.
2.47. Какая доля радиоактивных ядер кобальта, период полураспада которых равен 71,3 суток, распадется за месяц (30 суток)? 2.48. Найти постоянную распада и среднее время жизни радиоактивного 55Со, если его активность уменьшается на 4% за один час. 2.49. Сколько β-частиц испускает за один час 1,0 мкг нуклида 24Na. 2.50. Активность некоторого радионуклида уменьшается в 2,5 раза за 7 суток. Найти его период полураспада. 2.51. В начальный момент активность некоторого радионуклида времени составляла 10,8·106 Бк. Какова будет его активность по истечению времени, равной половине периода полураспада. 2.52. Активность радиоактивного препарата уменьшилась в 250 раз. Скольким периодам полураспада Т1/2 равен протекший промежуток времени. 2.53. Активность нуклида 24Na через 20 часов стала равной 1,0·109 Бк. Найти активность свежеприготовленного препарата и его удельную активность. 2.54. Для измерения активности была принята единица 1 кюри (Ки), 1 Ки = 3,7·1010 Бк, которая соответствовала активности 1 г 226Ra. Определить период полураспада 226Ra. 2.55. Ядра 235U наряду с a-распадом (период полураспада Т 1/2 = 8,91·108 лет) испытывают спонтанное деление (среднее время жизни t = 3·1017 лет). Оценить среднее количество ядер в 1 г чистого 235U, испытывающих спонтанный распад в течение одного часа. Сколько a-распадов происходит в том же образце за один час? 2.56. Показать, что удельная активность а любого радиоактивного нуклида, не зависит от времени. 2.57. Вычислить удельные активности нуклидов 24Na и 235U, периоды полураспада которых равны 15 часов и 7,1·108 лет соответственно. 2.58. Найти отношение удельной активности плутония 238Pu к удельной активности урана 236U. 2.59. 1 мг 226Ra испускает 3,61·107 α-частиц в секунду. Оценить промежуток времени (в годах), через который от первоначального количества останется одно ядро 226Ra. 2.60. Активность препарата, содержащего радионуклид 24Na, через 20 часов после приготовления стала равной 2,1·109 Бк. Найти активность свежеприготовленного препарата, учитывая, что удельная активность нуклида 24Na равна 3,22·1017 Бк/г. 2.61. Древесный уголь, обнаруженный на местах стоянок древних индейцев, обладает β-активностью, обусловленной наличием нуклида 14С и равной в среднем 12,9 распадов в минуту на 1 г углерода в образце. Активность 14С в живых деревьях не зависит от выбранного дерева и равна в среднем 15,3 распада в минуту на 1 г углерода в живых деревьях. Определить возраст стоянок. 2.62. Содержание трития в воде из некоторой глубокой скважины составляет 33% от того количества, которое содержится в свежей дождевой воде. Сколько времени прошло с того времени, когда вода, содержащаяся в скважине, выпала в виде дождя?
2.63. Считая, что в начальный момент ядер 90Y не было, найти отношение числа ядер 90Sr к числу ядер 90Y в источнике β-частиц 90Sr - 90Y спустя: а) сутки после изготовления; б) год после изготовления. Принять, что Т1/2 (90Sr) = 28,1 года, а Т1/2 (90Y) = 64,1 часа. 2.64. Образец 23Na облучается потоком тепловых нейтронов, в результате чего образуется 108 атомов 24Na в секунду. Определить максимальное число атомов 24Na, которое может образоваться при облучении данным потоком тепловых нейтронов. 2.65. Радионуклид 32Р, период полураспада которого Т 1/2 = 14,3 суток, образуется в ядерном реакторе с постоянной скоростью q = 3,1·109 ядер/с. Через сколько времени после начала образования этого радионуклида его активность станет А = 1,0·109 Бк. 2.66. Радионуклид 27Mg, который с периодом полураспада Т 1/2 = 8,5 минут превращается в стабильный нуклид 27Al, образуется с постоянной скоростью q = 1,0·1010 ядер/с. Какая масса нуклида 27Al образуется спустя месяц (30 дней) после начала его образования? 2.67. Препарат урана, массой 1,0 г, излучает 1,24·104 α-частиц в секунду. Найти его период полураспада. 2.68. Радионуклид 128I образуется с постоянной скоростью q = 7,48·109 ядер/с. Его активность через двадцать минут стала равной 3,23·109 с- 1. Чему равен период полураспада 128I? 2.69. Какая доля радиоактивного нуклида 35S распадется за вторую неделю (в течение второй недели) с момента изготовления препарата. 2.70. Радионуклид 32Р, период полураспада которого Т1/2=14,3 суток, образуется в ядерном реакторе с постоянной скоростью q = 5,1·109 ядер/с. Чему будет равна активность радионуклида через двадцать суток после начала облучения. 2.71. Найти постоянную распада и среднее время жизни радиоактивного нуклида 55Со, если его удельная активность составляет активность уменьшается на 4% в час. 2.72. Определить энергию, выделяющуюся при α-распаде 239Pu в течение одной секунды. Количество плутония 239Pu составляет один грамм. Энергия распада 5,14 МэВ. 2.73. Возможен ли α-распад полония 210Ро и железа 56Fe? 2.74. Выразить кинетическую энергию дочернего ядра, возникающего в результате α-распада материнского ядра с массовым числом А, если энергия распада равна Q α. Найти кинетическую энергию дочернего ядра при α-распаде ядра 210Bi. 2.75. Вычислить высоту центробежного барьера для α-частиц, вылетающих из ядра 222Rn с орбитальным моментом l =2. Оценить полную высоту потенциального барьера для таких α-частиц. 2.76. При α-распаде ядер 212Ро с первого возбужденного уровня (см. схему в задаче 2.21) наблюдается два конкурирующих процесса: непосредственное испускание α-частиц (длиннопробежная группа α-частиц) или же испускание α-частиц после перехода возбужденного ядра в основное состояние (основная группа α-частиц). При этом на каждые 1,0·106 α-частиц основной группы испускается в среднем 35 длиннопробежных α-частиц с первого возбужденного уровня. Найти среднее время τγ жизни возбужденного ядра по отношению к γ-излучению, если среднее время жизни этого уровня по отношению к испусканию длиннопробежных α-частиц τα = 1,6·10‑9 с.
2.77. Рассчитать энергию ядра отдачи при захвате электронов ядрами 37Ar. Изобразить графически энергетический спектр нейтрино. 2.78. Вычислить максимальную энергию ядра отдачи при β-распаде ядер трития. Определить максимальную энергию β-частиц и среднюю энергию нейтрино. Средняя энергия β-частиц равна 5,7 кэВ. 2.79. Покоящееся ядро нуклида 7Ве испытывает Е -захват. Дочернее ядро при этом оказывается в основном состоянии. Вычислить энергию распада и определить кинетическую энергию, которую приобретает дочернее ядро. 2.80. Определить кинетическую энергию β-частицы при распаде ядра 204Та, если дочернее ядро остается в покое. 2.81. Изомерное ядро 69mZn переходит в основное состояние, испуская γ-квант с энергией 0,436 МэВ. Вычислить кинетическую энергию образующегося ядра. 2.82. С какой скоростью и в каком направлении следует перемещать источник γ-излучения, чтобы полностью компенсировать в поглотителе гравитационное изменение энергии γ-кванта, если источник находится над поглотителем на высоте 20 м. Указание: вспомнить эффект Допплера. 2.83. За один час измерений зарегистрировано 12000 импульсов. Вычислить скорость счета и абсолютную и относительную погрешности определения этой величины с доверительной вероятностью 0,68 и 0,95. 2.84. Интенсивность регистрации фона равна интенсивности исследуемого излучения. Сколько частиц необходимо зарегистрировать, чтобы статистическая погрешность определения интенсивности исследуемого излучения не превышала 5%, если измерения выполняются оптимальным образом. 2.85. В эксперименте по определению возраста древних предметов с помощью радиоуглеродного метода (см. задачу 2.5), найденных при археологических раскопках, обнаружено, что скорость счета составляет 14 импульсов в минуту, а скорость счета фона – 9,5 импульсов в минуту. Сколько времени займут измерения для оценки возраста предметов с точностью 5%. 2.86. Счетчик имеет разрешающее время τ = 8·10-6 с. При какой скорости счета просчеты не будут превышать 2%. 2.87. При облучении детектора источником №1 зарегистрированная счетчиком скорость счета составляла Ответы 2.43. 4,4·10-5; 0,233. 2.44. 0,205. 2.45. 0,642; 0,11. 2.46. 2.2·1017. 2.47. 0,253. 2.48. 0,021 час -1; 24,5 часа. 2.49. 1,1·1015. 2.50. 5,3 суток. 2.51. 7,64·106 Бк. 2.52. ≈ 8 Т 1/2. 2.53. 2,5·109 Бк; 3,2·1017 Бк/г. 2.54. 1580 лет. 2.55. 2,28·108; ≈1. 2.56. а = λ/Мат. 2.57. 3,2·1017 Бк/г; 7,9·104 Бк/г. 2.58. 2,65·105. 2.59. 9,93·104 ≈ 105 лет. 2.60. 5,3·109 Бк. 2.61. 1370 лет. 2.62. ≈ 20 лет. 2.63. а) 1,68·104; б) 3840. 2.64. 7,79·1012. 2.65. 9,54 суток. 2.66. 2,6·1016 ядер; 1,2·10-6 г. 2.67. 4,5·109 лет. 2.68. 24,5 мин. 2.69. 5,15·10-2. 2.70. 3,17·109 Бк. 2.71. 0,041 час -1; 24,5 час. 2.72. 1,19·1010 МэВ. 2.73. Да; нет. 2.74. 9,47·10-2 МэВ. 2.75. 0,032 и 28,4 МэВ. 2.76. 5,6·10-14 с. 2.77. 9,6 эВ;. 2.78. 1,8 эВ; 12,9 кэВ; 7,2 кэВ. 2.79. 0,862 МэВ; 57 эВ. 2.80. 0.21 МэВ. 2.81. 1,48 эВ. 2.82. 6,5·10-5 см/с; вверх. 2.83. Ядерные реакции Символическая запись ядерной реакции:
где С – составное ядро. Энергетическая схема ядерной реакции:
которая протекает с образованием возбужденного составного
Экзоэнергетическая реакция представлена на схеме а); на схеме б) представлена эндоэнергетическая реакция. Энергия, которая может быть передана для возбуждения составного ядра С, образующегося в процессе (3.1):
ε а (С) – энергия связи частицы а относительно составного ядра С;
Построение векторной диаграммы импульсов для частиц, участвующих в ядерной реакции A (a, b) B, показано на рис. 3.3. Частица А (ядро-мишень) в ЛСК покоится.
где Пороговая кинетическая энергия (Та)пор налетающей частицы а в ЛСК, при которой становится возможной эндоэнергетическая ядерная реакция:
Ядро-мишень А в ЛСК покоится.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 951; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.126.199 (0.016 с.) |

 В результате активации образовалось N 0 = 10 радиоактивных ядер. Какова вероятность распада точно 5 ядер за время t = Т 1/2?
В результате активации образовалось N 0 = 10 радиоактивных ядер. Какова вероятность распада точно 5 ядер за время t = Т 1/2? .
. Предполагается провести 2000 измерений активности препарата в течение одинаковых промежутков времени. Среднее число импульсов за время одного измерения равно 10,0. Считая время измерения малым по сравнению с периодом полураспада исследуемого радионуклида, определить число измерений, в которых следует ожидать точно 10 и 5 импульсов.
Предполагается провести 2000 измерений активности препарата в течение одинаковых промежутков времени. Среднее число импульсов за время одного измерения равно 10,0. Считая время измерения малым по сравнению с периодом полураспада исследуемого радионуклида, определить число измерений, в которых следует ожидать точно 10 и 5 импульсов. ,
, 76;
76; .
. Среднее значение скорости счета импульсов от исследуемого радионуклида с большим периодом полураспада составляет 100,0 имп./мин. Определить вероятность получения 105 имп./мин. И вероятность того, что абсолютное отклонение от среднего числа имеет значение, большее 5,0 имп./мин.
Среднее значение скорости счета импульсов от исследуемого радионуклида с большим периодом полураспада составляет 100,0 имп./мин. Определить вероятность получения 105 имп./мин. И вероятность того, что абсолютное отклонение от среднего числа имеет значение, большее 5,0 имп./мин.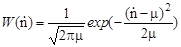 .
.
 .
. = 0 и до
= 0 и до 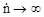 равняется единице. Тогда
равняется единице. Тогда
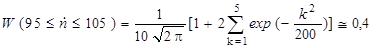 .
.

 Задача 2.37
Задача 2.37 .
.

 ,
,
 Счетчик, находящийся в поле исследуемого излучения, зарегистрировал 3600 импульсов за 10 мин. Найти: а) среднюю квадратичную погрешность в скорости счета; б) продолжительность измерения, обеспечивающую определение скорости счета с погрешностью 1,00%.
Счетчик, находящийся в поле исследуемого излучения, зарегистрировал 3600 импульсов за 10 мин. Найти: а) среднюю квадратичную погрешность в скорости счета; б) продолжительность измерения, обеспечивающую определение скорости счета с погрешностью 1,00%. .
. .
.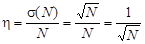 .
. .
. .
.
 При изучении интенсивности исследуемого облучения (вместе с фоном) счетчик зарегистрировал 1700 имп. за 10,0 мин. Отдельное измерение фона дало 1800 имп. за 15,0 мин. Найти скорость счета, имп./мин, обусловленную исследуемым облучением, и ее среднюю квадратичную погрешность.
При изучении интенсивности исследуемого облучения (вместе с фоном) счетчик зарегистрировал 1700 имп. за 10,0 мин. Отдельное измерение фона дало 1800 имп. за 15,0 мин. Найти скорость счета, имп./мин, обусловленную исследуемым облучением, и ее среднюю квадратичную погрешность.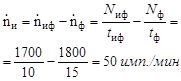
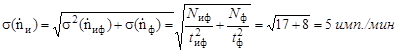
 Задача 2.40
Задача 2.40
 ,
, ;
; ;
; .
.

 .
.
 следует, что
следует, что .
.
 .
. Счетчик Гейгера-Мюллера с разрешающим временем τ = 0,20 мс зарегистрировал 3,0·104 имп./мин. Оценить среднее число частиц, прошедших через счетчик в мин.
Счетчик Гейгера-Мюллера с разрешающим временем τ = 0,20 мс зарегистрировал 3,0·104 имп./мин. Оценить среднее число частиц, прошедших через счетчик в мин. Любой счетчик ядерного излучения после регистрации попавшей частицы затрачивает некоторый промежуток времени τ для восстановления своих свойств. Время τ – время восстановления является одной из основных характеристик счетчика ядерных частиц. Если в течение этого промежутка времени в счетчик попадает частица, то она не может быть зарегистрирована. Рисунок поясняет это явление. Частицы 1, 2, 4 будут зарегистрированы, а частица 3 – нет (просчитана), так как она попала в счетчик в интервал времени τ восстановления свойств счетчика.
Любой счетчик ядерного излучения после регистрации попавшей частицы затрачивает некоторый промежуток времени τ для восстановления своих свойств. Время τ – время восстановления является одной из основных характеристик счетчика ядерных частиц. Если в течение этого промежутка времени в счетчик попадает частица, то она не может быть зарегистрирована. Рисунок поясняет это явление. Частицы 1, 2, 4 будут зарегистрированы, а частица 3 – нет (просчитана), так как она попала в счетчик в интервал времени τ восстановления свойств счетчика. – число просчитанных (незарегистрированных) частиц за суммарное мертвое время
– число просчитанных (незарегистрированных) частиц за суммарное мертвое время ,
,
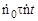 .
.
 .
.
 имп./мин.
имп./мин. Какая доля частиц, проходящих через счетчик с разрешающим временем τ =1,0 мкс, не будет зарегистрирована при скорости счета
Какая доля частиц, проходящих через счетчик с разрешающим временем τ =1,0 мкс, не будет зарегистрирована при скорости счета  и 1,0·105 имп./мин.
и 1,0·105 имп./мин. .
. имп./с. При облучении источником №2 скорость счета
имп./с. При облучении источником №2 скорость счета  имп./с. Скорость счета при облучение детектора одновременно обоими источниками составила
имп./с. Скорость счета при облучение детектора одновременно обоими источниками составила  =1673 имп/с. Вычислить разрешающее время счетчика.
=1673 имп/с. Вычислить разрешающее время счетчика. =200 мин- 1; Δ(68)≈2 мин- 1и Δ(95)≈4 мин- 1; δ(68)≈1% и δ(95)≈2%. 2.84. 9600. 2.85. 19 часов. 2.86. 2,5·10-3 с -1. 2.87. 9,7·10‑5≈10‑4 с.
=200 мин- 1; Δ(68)≈2 мин- 1и Δ(95)≈4 мин- 1; δ(68)≈1% и δ(95)≈2%. 2.84. 9600. 2.85. 19 часов. 2.86. 2,5·10-3 с -1. 2.87. 9,7·10‑5≈10‑4 с.  ,
,
 ядра
ядра  , показана на рис. 3.1. На этом рисунке:
, показана на рис. 3.1. На этом рисунке:  и
и  - сумма энергий покоя частиц a и A до и после реакции, т.е. все массы выражены в энергетических единицах;
- сумма энергий покоя частиц a и A до и после реакции, т.е. все массы выражены в энергетических единицах; 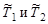 - суммарные кинетические энергии частиц до и после реакции в СЦИ (система центра инерции); Q - энергия реакции:
- суммарные кинетические энергии частиц до и после реакции в СЦИ (система центра инерции); Q - энергия реакции: ;
;
 и
и  - энергии связи частиц a и b в составном ядре
- энергии связи частиц a и b в составном ядре 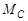 .
. ,
,
 - кинетическая энергия частицы а в СЦИ.
- кинетическая энергия частицы а в СЦИ.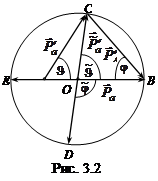
 Построение векторной диаграммы импульсов для упругого рассеяния нерелятивистской частицы массой
Построение векторной диаграммы импульсов для упругого рассеяния нерелятивистской частицы массой  на первоначально покоившейся частице массой
на первоначально покоившейся частице массой  в ЛСК (лабораторная система координат) приведена на рис. 3.2. Величины, относящиеся к СЦИ, обозначены сверху знаком “~” (тильда). Отрезок AB – представляет импульс
в ЛСК (лабораторная система координат) приведена на рис. 3.2. Величины, относящиеся к СЦИ, обозначены сверху знаком “~” (тильда). Отрезок AB – представляет импульс 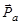 налетаюшей частицы a в ЛСК. Точка О делит отрезок AB на две части в отношении AO:OB = ma:MA. Отрезки AC и CB представляют импульсы
налетаюшей частицы a в ЛСК. Точка О делит отрезок AB на две части в отношении AO:OB = ma:MA. Отрезки AC и CB представляют импульсы  и
и  частиц a и A после рассеяния в ЛСК. Отрезки OB и OE - импульсы
частиц a и A после рассеяния в ЛСК. Отрезки OB и OE - импульсы  и
и  частиц a и A до столкновения в СЦИ. Соответственно отрезки OC и OD представляют импульсы
частиц a и A до столкновения в СЦИ. Соответственно отрезки OC и OD представляют импульсы  и
и  частиц a и A после столкновения в СЦИ. Углы
частиц a и A после столкновения в СЦИ. Углы  и φ – углы рассеяния частиц a и A в соответствующих системах координат.
и φ – углы рассеяния частиц a и A в соответствующих системах координат. ,
, 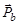 и
и  - импульсы в ЛСК налетающей частицы и частиц, возникающих в результате реакции, а
- импульсы в ЛСК налетающей частицы и частиц, возникающих в результате реакции, а  ,
,  =
=  =
=  - те же импульсы в СЦИ. О – центр окружности с радиусом, равным величине импульса
- те же импульсы в СЦИ. О – центр окружности с радиусом, равным величине импульса  ,
,
 - приведенная масса возникающих частиц; Q - энергия реакции (см. (3.3)). Отрезок AB представляет импульс
- приведенная масса возникающих частиц; Q - энергия реакции (см. (3.3)). Отрезок AB представляет импульс 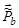 и
и  образовавшихся частиц b и B в СЦИ. Углы
образовавшихся частиц b и B в СЦИ. Углы 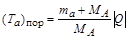 .
.



