
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь спектров излучения (поглощения)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Со строением вещества
Одним из первых экспериментальных результатов, не нашедших объяснения с помощью законов классической физики является спектр излучения отдельных атомов и молекул, находящихся в возбуждённом состоянии, а также сплошной спектр излучения твёрдого тела (типа нити накаливания). Было замечено, что отдельные спектральные линии расположены не беспорядочно, как это может показаться на первый взгляд. Было также установлено, что: а) для одного и того же химического элемента расположение линий одинаково как для спектров излучения так и для спектров поглощения и не зависит от температуры; б) расположение спектральных линий различных элементов различно; в) при конденсации вещества (переход пар→жидкость→твёрдое тело) спектр становится сплошным. В 1885 г. физикам Бальмеру и Ридбергу удалось установить, что длины волн излучения атома водорода в видимой области спектра (серия Бальмера, см. рис. 3) могут быть точно описаны формулой
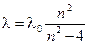
где n (для серии Бальмера) - 3, 4, 5, …;
Или в волновых числах
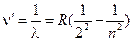 ; ;
где n=3, 4, 5, …; R=109737,309±0,012 см-1 - постоянная Ридберга. Для n=3 λ=0,6563 мкм - красная линия в спектре (Hα); n=4 λ=0,4861 мкм - голубая линия (Hβ);
n=6 λ=0,4101 мкм При n=∞ λ=4/R≈0,5646 мкм - граница серии Бальмера, причём по Дальнейшие исследования показали, что в спектре водорода имеется ещё несколько серий излучения, невидимых человеческому глазу, которые лежат в УФ и ИК областях спектра: в УФ – Лаймана:
 , n=4, 5, 6, …; , n=4, 5, 6, …;
Брэкета: Пфунда: Общая формула для них (обобщённая формула Бальмера):
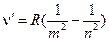 , ,
где при m=1, а n=2, 3, 4, … - серия Лаймана; m=2, а n=3, 4, 5 … - видимая область Бальмера и т.д. Успехи квантовой механики и предложенная Бором в 1911 году теория строения атома водорода позволила объединить закономерности, наблюдаемые в спектрах излучения и поглощения атома водорода, а в последствии и многоэлектронных атомов. Предложенная Бором квантово-механическая модель атома и сейчас является наиболее доступной в понимании строения атома, хотя и заменена более совершенной квантовой моделью Гейзенберга, Шредингера, Дирака, Зоммерфельда и др. Бор создал свою теорию водородоподобного атома, основанную на следующих постулатах: 1. Электрон вращается вокруг протона в атоме водорода, совершая равномерное движение по круговой орбите под действием кулоновской силы и в соответствии с законами Ньютона. 2. Из всех возможных орбит являются разрешёнными только те, для которых момент импульса электрона равен целому, умноженному на
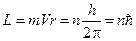 ; n=1, 2, 3 …, ; n=1, 2, 3 …,
где h - постоянная Планка; n - номер орбиты (главное квантовое число). 3. При движении электрона по разрешённой орбите атом не излучает энергию. 4. При переходе электрона с орбиты с энергией Ei на другую орбиту с энергией Ej и Ej< Ei излучается фотон с энергией
и частотой
 [Гц] [Гц]
См. рис. 4 (переход A→B с орбиты с номером n=5 на n=4), т.е. излучается фотон с частотой
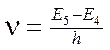 [Гц] [Гц]
С другой стороны, если фотон с энергией Таков в общих чертах механизм образования линейчатых спектров испускания и поглощения. На основе постулатов, а также с использованием законов классической и квантовой механики Бор установил, что радиус орбиты электрона в водородоподобном атоме может принимать лишь ряд дискретных значений:
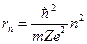 , ,
n=1, 2, 3, 4...; m - масса электрона; e - заряд электрона; Z - число протонов в ядре ZH=1 Для первой неизлучающей орбиты водородоподобного атома (Z=1, n=1)
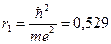 Å, (1Å=10-4 мкм) Å, (1Å=10-4 мкм)
Энергия, которой обладает электрон, находясь на неизлучающей орбите, в теории Бора определяется выражением
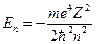 , n=1, 2, 3 … , n=1, 2, 3 …
Тогда для первой орбиты водородоподобного атома (Z=1, n=1)
E1=-13,6 эВ - минимальная энергия, необходимая для ионизации атома водорода. При переходе атома водорода из состояния n в состояние m (n>m) → En>Em испускается квант света с энергией
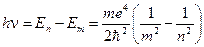
R - постоянная Ридберга. Таким образом, мы пришли к обобщённой эмпирической формуле Бальмера через квантово-механическую модель атома водорода, которая хорошо согласуется с экспериментальными результатами. Схема энергетических уровней, определяемых выражением (15) приведена на рис. 7.
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.173.72 (0.008 с.) |

 - некоторая константа;
- некоторая константа; - длина волны излучения.
- длина волны излучения.
 n=5 λ=0,4340 мкм
n=5 λ=0,4340 мкм , n=2, 3, 4, …;
, n=2, 3, 4, …;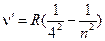 , n=5, 6, 7, …;
, n=5, 6, 7, …;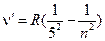 , n=6, 7, 8, … и др.
, n=6, 7, 8, … и др. :
: [эВ]
[эВ]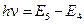 падает на атом, то он может быть поглощён, и электрон перейдет с орбиты с номером n=4 на орбиту с номером n=5 или (E4→E5).
падает на атом, то он может быть поглощён, и электрон перейдет с орбиты с номером n=4 на орбиту с номером n=5 или (E4→E5).
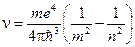 ;
;  ,
,


