Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение первого закона термодинамикиСодержание книги
Поиск на нашем сайте
К химическим процессам Любая химическая реакция сопровождается выделением или поглощением энергии. Потенциальная энергия, скрытая в химических связях, и кинетическая энергия (поступательного и других видов движения атомов и молекул) изменяются в ходе химической реакции. Химическая реакция как система получает энергию извне на разрыв химических связей исходных реагентов и выделяет энергию в окружающую среду при образовании новых химических связей в молекулах – продуктах реакции (табл. 3). Представим энергетические изменения на примере горения водорода в кислороде (рис. 43).
При образовании новых химических связей энергия выделяется. Это кинетическая энергия движения молекул – продуктов реакции. Часть внутренней энергии, которая была скрыта в химических связях молекул водорода и кислорода, превратилась в энергию поступательного и других видов движения молекул воды: DН =2×(+436)+498.4 + 2×(-427,8) +2×(-498.7) = -482,6 кДж. Величина DН = -482,6 кДж эквивалентна энергии движущихся молекул воды. Именно эта кинетическая энергия определяет рост температуры в процессе горения водорода в среде кислорода.
Т а б л и ц а 3 Энергии связей некоторых двух- и трехатомных молекул
Термохимические расчеты Различают экзо- и эндотермические реакции. Химические реакции, сопровождающиеся выделением или поглощением энергии в форме теплоты, называются соответственно экзотермическими и эндотермическими реакциями. Энтальпия реакции Пример. Чему равна энтальпия реакции образования фтороводорода, если известны энергии связей исходных веществ и продукта реакции.
Решение Энтальпия DН реакции вычисляется по термохимическому уравнению: H2(г) + F2(г) = 2HF(г); DН=? Форма уравнения химической реакции, указывающая агрегатные состояния участников процесса и его энтальпию, называется термохимическим уравнением. Для разрыва химических связей в молекулах Н2 и F2 требуется затратить (согласно табл. 3) 436 и 159 кДж энергии соответственно. Это эндотермический процесс. Значения энергии берутся со знаком (+). При образовании химических связей в молекулах НF выделяется энергия. Это экзотермический процесс. Перед значениями энергии связи ставится знак (-) (-568,5 кДж).
DН= Е(Н - Н) + Е(F - F) +2Е(Н - F) DН= [436 +159] +2 [-568,5] = - 542кДж.
Образование двух молекул НF приводит к выделению 542 кДж энергии. Реакция экзотермическая. Пример. Оксид азота NO образуется при грозовых электрических разрядах в облаках. Чему равна энтальпия реакции окисления 84 г азота атмосферным кислородом? Решение N2(г) + О2(г) = 2NO(г), D Н =? E св +945,3 +498,4 2 (–632) Используются данные, приведенные в табл.3. D Н 1 = [945,3 + 498.4] + 2 [–632] = 179.7 кДж. При окислении 84 г N2 (3моль азота): D Н 2 = 3×179.7 = 539.1 кДж. Окисление 84 г азота в избытке кислорода сопровождается поглощением из окружающей среды 539,1 кДж энергии. Реакция эндотермическая. Приведенные в примерах расчеты D Н по энергиям химических связей имеют ограниченное применение и используются в основном для двух- и трехатомных молекул. В термохимии основными данными для проведения термохимических расчетов служат энтальпии образования сложных соединений из простых веществ Под простыми веществами подразумеваются все химические элементы периодической системы в кристаллической форме, характерной для металлов (за исключением ртути), и молекулярной форме для неметаллов (за исключением благородных газов) в том агрегатном состоянии, которое для них характерно при внешнем давлении 1 атм. Для внешнего давления, равного 1 атм и температуре T = 298.15 К, в справочных таблицах термодинамических величин (см. приложение) даются стандартные энтальпии образования соединенийразной степени сложности. Например, энтальпия образования
С(графит) + О2(г) = СО2(г); С(графит) и О2(газ) – простые вещества. Энтальпия образования всех простых веществ принята за начало отсчета и равна нулю. Задачей термохимии является расчет энтальпий химических реакций Основной закон термохимии (закон Гесса, 1836 г.) в современной интерпретации утверждает, что энтальпия реакций, протекающих либо при V,T = const, либо p,T = const не зависти от промежуточных стадий, а определяется лишь начальным и конечным состояниями системы. Например, экспериментально невозможно определить значение D H 1реакции: С(гр) + так как при сжигании графита, как правило, образуется смесь оксидов (СО2 и СО). В соответствии с законом Гесса можно преодолеть это затруднение, измерив экспериментально (в калориметре) энтальпии следующих реакций: С(гр) + О2(г) ® СО2(г); D H 2 = - 393,51 кДж/моль, СО(г) + Представим возможные пути превращений исходных соединений.
Поскольку D H есть функция состояния системы, в которой происходят реакции, то в соответствии с законом Гесса независимо от того, идет реакция по первому или второму пути: D H 1 = D H 2 + D H 3 или D H 2 = D H 1 - D H 3 = (- 393,51) - (- 282,99) = - 110, 52 кДж. Именно столько энергии выделяется (экзотермический процесс) при образовании 1 моль СО из С(гр) и 1/2О2(г). Эта величина вычислена теоретически. В соответствии с законом Гесса с термохимическими уравнениями можно обращаться как с алгебраическими. Их можно складывать друг с другом или вычитать из одного уравнения другое. Именно эти операции используют при вычислении энтальпии реакции Воспользуемся табличными данными термохимических величин, приведенных в приложении, для вычисления энтальпии реакции разложения карбоната кальция: СаСО3(т) ® СаО(т) + СО2(г);
Для того чтобы вычислить
В том, что именно такую алгебраическую операцию нужно совершить, можно убедиться, если записать реакции образования участников процесса: Са(т) + 1/2О2(г) ® СаО(т); С(т) + О2(г) ® СО2(г); С(т)+3/2О2(г)+С(т)®СаСО3(т); При вычитании из алгебраической суммы первых двух уравнений третьего и выполнении необходимых сокращений и переносов получим: СаСО3(т) ® СаО(т) + СО2(г); [(- 635.1) + (- 393.51)] - [- 1206], СаСО3(т) ® СаО(т) + СО2(г); Dr Н 0(298) = 177.39 кДж. Второй закон термодинамики Движущей силой любого процесса, совершающегося в системе, является ее неустойчивость. Только в этом случае система самопроизвольно переходит из неустойчивого в устойчивое состояние. Брусок, расположенный на определенной высоте, самопроизвольно падает на поверхность пола, но никогда не вернется в исходное положение самопроизвольно. Заметим, что потенциальная энергия падающего бруска спонтанно уменьшается. Возможно, направление самопроизвольного процесса связано со стремлением системы к минимуму энергии? Но в соответствии с первым законом термодинамики в окружающей среде происходит самопроизвольное возрастание энергии на ту же величину. Другими словами, изменение энергии системы и окружающей среды не может служить критерием направления самопроизвольного процесса.
В конце XIX и начале ХХ вв. два выдающихся физика-теоретика Р. Клаузиус и В. Томсон в своих исследованиях установили, что полное количество энергии в любом процессе должно сохраняться в соответствии с первым законом термодинамики, а распределение имеющейся энергии осуществляется необратимым образом. Последняя фраза означает, что энергия превращается самопроизвольно в менее ценные формы. Одна из многих формулировок второго закона термодинамики утверждает: невозможен круговой (циклический) процесс, имеющий единственным своим результатом превращение теплоты в работу. Поршни в двигателе автомобиля должны совершать циклически повторяющиеся движения, чтобы заставить вращаться коленчатый вал. При этом в атмосферу выбрасываются горячие выхлопные газы. Следовательно, часть энергии, выделяющаяся при сжигании топлива, расходуется не на движение автомобиля, а на нагревание окружающей среды. И эта энергия не может быть превращена в работу. В начале XIX в. французский инженер С. Карно доказал, что идеальная тепловая машина, действующая циклически (цикл Карно), не может полностью превратить теплоту в работу. Позже математическое выражение коэффициента полезного действия машины h, работающей по циклу Карно, дал соотечественник Карно, инженер Б. Клапейрон: h В двигателе современного автомобиля температура сгорания топлива достигает 14000С (1673 К). Выхлопные газы, выбрасываемые в атмосферу, имеют температуру около 10000С (1273 К). Коэффициент полезного действия такого двигателя составляет: h = (1673-1273)/1673 = 0,24 или 24%.
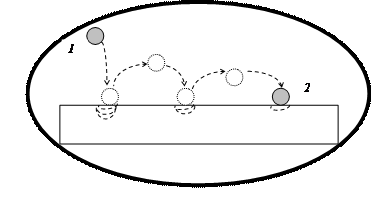
Энтропия Обратимся к модели самопроизвольного необратимого превращения энергии на примере механической модели, предложенной Эткинсом (рис. 44). Потенциальная энергия падающего тела превращается в энергию движения микрочастиц поверхности пола. Энергия системы остается постоянной, происходит лишь ее перераспределение. Обратный процесс перемещения тела из состояния 2 в состояние 1 невозможен. Тело самопроизвольно не вернется в исходное состояние, т.к. частицы, расположенные на поверхности пола, рассеяли полученную энергию по всей поверхности пола в результате межмолекулярных соударений.
Рис. 44. Модель рассеяния энергии (увеличения беспорядка) в результате падения шарика на поверхность пола. Цифрами обозначены: 1 - начальное, 2 - конечное состояние системы. Стрелки указывают направление самопроизвольного (необратимого) процесса. Система изолирована от окружающей среды
Обычно математическое выражение второго закона термодинамики дается на примере цикла Карно или выводится с использованием принципа Каратеодори. Мы ограничимся следующим уравнением второго закона термодинамики
принимая его как закон, который, как и любой фундаментальный закон, не выводится. Для термодинамически равновесного (обратимого) процесса уравнение (4.22) принимает вид: dS обр. В термодинамически неравновесном (необратимом) процессе dSнеобр. Изменение энтропии как критерий направления процесса применим к изолированным системам. Так как изолированная системане обменивается энергией с окружающей средой, для нее dQ = 0 и, соответственно, для состояния термодинамического равновесия в изолированной системе
dS сист. = 0 (4.25) для необратимого процесса, протекающего в изолированной системе dS сист. > 0. (4.26) Одна из формулировок второго закона термодинамики гласит: любой необратимый процесс характеризуется увеличением энтропии изолированной системы (dS сист. >0) и любой обратимый процесс характеризуется неизменностью энтропии изолированной системы (dS сист. =0). На примере изолированной системы, состоящей из горячего и холодного тел (рис. 45), покажем, что процессы обмена энергией в форме теплоты между телами сопровождаются ростом энтропии. Изменение энтропии системы равно сумме изменений энтропии входящих в состав данной системы тел. dS сист. = dS1 + dS2 или dS сист. Горячее тело при Т 1 обменивает с холодным телом, находящимся при температуре Т 2, бесконечно малое количество энергии. Количество теплоты δQ настолько малое, что температура тел практически не меняется и Т 1 >> Т 2.
Рис. 45. Обмен энергией горячего (Т1) и холодного (Т2) тел в изолированной системе
В соответствии с принятой в термодинамике шкалой δQ < 0 для горячего тела и δQ > 0 для холодного. Следовательно, в уравнении (4.27) отношение
Таким образом, только самопроизвольные процессы передачи тепла от горячего тела к холодному протекают в изолированной системе.
Функция Гиббса Второй закон термодинамики, опирающийся на концепцию энтропии как критерий самопроизвольного процесса в изолированной системе, применим к любым системам, при условии учета всех без исключения внешних объектов, которые обмениваются с системой энергией. Фактически это означает рассмотрение изолированной совокупности тел система – окружающая среда. При этом приведенный ниже расчет позволяет судить о направлении самопроизвольного процесса только по параметрам системы. dS = dS окр. среда + dS сист. = dQ окр. среда/ Т окр. среда + dS сист. ³ 0 (4.28) В соответствии с законом сохранения энергии количество энергии в форме теплоты, поступившее из окружающей среды в систему, равно теплоте, полученной системой:
- dQ окр. среда = dQ сист.. (4.29) Если процесс в системе (например, химическую реакцию в сосуде) проводят при постоянной температуре, равной температуре окружающей среды, то Т окр.среда = Т сист. = Т. (4.30) Преобразуем уравнение (4.28), учитывая уравнения (4.29) и (4.30) (dS сист. - dQ сист./ Т) ³ 0. (4.31) Получили уравнение (4.31), не содержащее параметров, относящихся к окружающей среде. Оно отражает направление самопроизвольного процесса или состояние термодинамического равновесия только через свойства системы, поэтому, отбросив индексы (все они относятся к системе), запишем: (dS - dQ / Т) ³ 0. (4.32) Если процесс проводят при постоянной температуре и давлении (Т,р = const), а это наиболее часто встречающийся случай проведения физико-химических процессов, то выражение первого закона термодинамики dQ = dU + pdV примет вид dQр = d(U + pdV) или dQр = dН. Соответственно уравнение (4.32) запишется: (dН – TdS) £ 0. Поскольку энтропия и энтальпия являются функциями состояния системы, их разность также является функцией состояния. d (Н – TS) £ 0, разность H – TS обозначим символом G. Функция состояния системы G = H – TS, впервые введенная Гиббсом, носит название функции Гиббса. По изменению функции Гиббса dG = dН – TdS £ 0 (4.33) можно судить о течении самопроизвольного процесса в исследуемой системе, происходящего при р,Т = const. Интегрируем уравнение (4.33)
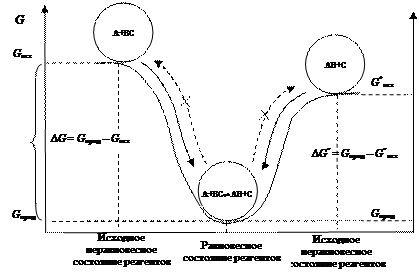
G 2 – G 1 = (H 2 – H 1) – T (S 2 – S 1), D G = D H – T D S. (4.34) Для любой химической реакции изменение функции Гиббса служит критерием направления химического превращения. Если D G < 0, самопроизвольный процесс происходитв направлении: исходные вещества ® продукты реакции. Если D G > 0, процесс идет в направлении: продукты реакции ® исходные вещества. Если D G = 0, система находится в состоянии термодинамического равновесия. Ответ на вопрос, почему идут химические реакции, очевиден, – реакционная система стремится перейти в устойчивое состояние. Достижение химического равновесия между реагентами А, ВС и продуктами реакции АВ и С А + ВС ⇆ АВ + С подобно движению шарика по склону ложбины (рис. 46). Движение может осуществляться самопроизвольно со стороны веществ (А + ВС) или со стороны веществ (АВ + С). Для определения направления смещения равновесия рассчитывают значения и по знаку
Рис. 46. Модель, демонстрирующая направление термодинамически разрешенного процесса, аналогична скатыванию шара в ложбину (самопроизвольный процесс)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.2.6 (0.01 с.) |

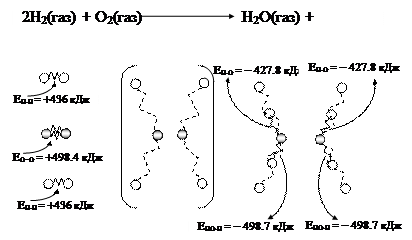 Рис. 43. Модель превращения потенциальной энергии, скрытой в химических связях, в кинетическую энергию на примере появления интенсивного колебательного движения молекул – продуктов реакции
Рис. 43. Модель превращения потенциальной энергии, скрытой в химических связях, в кинетическую энергию на примере появления интенсивного колебательного движения молекул – продуктов реакции равна количеству энергии в форме теплоты, выделяющейся или поглощающейся в результате химического процесса при постоянных р = 1 атм и температуре Т.
равна количеству энергии в форме теплоты, выделяющейся или поглощающейся в результате химического процесса при постоянных р = 1 атм и температуре Т. (f – formation). Энтальпия образования
(f – formation). Энтальпия образования  СО2(г) = - 393.51 кДж/моль относится к реакции
СО2(г) = - 393.51 кДж/моль относится к реакции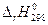 по табличным значениям
по табличным значениям  О2(г) ® СО(г); D H 1 =?
О2(г) ® СО(г); D H 1 =?
 или h
или h  .
.
 , (4.22)
, (4.22) (4.23)
(4.23)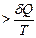 . (4.24)
. (4.24)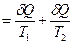 . (4.27)
. (4.27)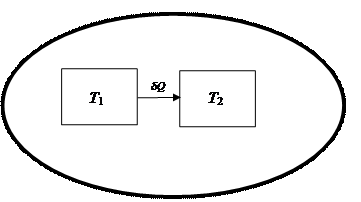
 , а
, а  . По абсолютной величине
. По абсолютной величине  , следовательно
, следовательно >0.
>0. ,
, , подставляют в уравнение
, подставляют в уравнение 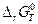 =
=