
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства термодинамической системыСодержание книги
Поиск на нашем сайте
Системе присущи такие свойства, как объем V, давление р, температура Т, концентрация сi, теплоемкость Ср или CV, внутренняя энергия U, а совокупность свойств определяет состояние системы. Если изменилось состояние системы, изменяются её свойства. Изменение состояния системы называется процессом. Подчеркнем, что изменение свойств не зависит от пути перехода системы из начального состояния в конечное. Между свойствами системы существуют определенные функциональные связи.Например, уравнение состояния идеального газа Важнейшими понятиями в термодинамике являются внутренняя энергия, теплота, теплоемкость, работа. Обмен внутренней энергией U термодинамической системы (в дальнейшем термодинамическую систему будем называть просто системой) с окружающей средой осуществляется либо в форме работы А, либо в форме теплоты Q, либо одновременно в обеих формах. Подчеркнем, что термодинамика рассматривает только две формы передачи энергии – теплоту и работу и не рассматривает, например, обмен системы энергией с окружающей средой посредством электромагнитного излучения.
Внутренняя энергия Полная энергия системы включает: 1) энергию направленного перемещения системы в пространстве как целого; 2) энергию системы в гравитационном и электромагнитном полях; 3) внутреннюю энергию системы U. В химии рассматривают неподвижные системы в постоянном внешнем поле. В таких условиях изменение энергетического состояния системы определяется изменением её внутренней энергии U. Внутренняя энергия U есть сумма кинетической S Е кин. и потенциальной S Е пот. энергии всех микрочастиц системы. U = S Е кин. + S Е пот. Кинетическая энергия как составляющая часть внутренней энергии – это энергия различного вида движения микрочастиц системы. Потенциальная энергия как составляющая внутренней энергии – этоэнергия межмолекулярного и внутримолекулярного взаимодействия. Например, нагревание жидкой воды до температуры кипения увеличивает кинетическую энергию системы (скорость движения молекул). Когда жидкость кипит при постоянной температуре и давлении (р,Т = const), кинетическая энергия не увеличивается, несмотря на то, что нагреватель продолжает передавать энергию в форме теплоты системе (жидкость – пар). Энергия нагревателя расходуется на увеличение потенциальной энергии S Е пот. пара, равной теплоте испарения Q исп.. Для отрыва молекул с поверхности жидкости требуется затратить энергию нагревателя, чтобы преодолеть силы межмолекулярного сцепления в жидкой воде. Температура не будет изменяться, пока не испарится последняя капля жидкости.
Химическая реакция, например реакция горения водорода в кислороде в калориметрической бомбе, позволяет превратить потенциальную энергию (энергию притяжения и отталкивания химически связанных атомов в молекулах) в кинетическую энергию (энергию движения молекул продуктов реакции). Важным свойством идеального газа является независимость его внутренней энергии от объема и давления
Этот факт экспериментально был доказан Джоулем. Из опытов Джоуля следует, что внутренняя энергия идеального газа является функцией только температуры:
Если система в начальном состоянии обладала внутренней энергией U 1 при температуре Т 1 и перешла в конечное состояние U 2 при температуре Т 2, то изменение внутренней энергии будет определяться разностью: D U = U 2 - U 1 (4.8)
Теплота Теплота Q есть форма передачи энергии от одного тела другому посредством соударения микрочастиц, составляющих тела (рис. 37). Интенсивное движение микрочастиц от горячего к холодному телу распространяется через границу прижатых друг к другу тел. Теплота является микрофизической характеристикой процесса передачи энергии. Если контакта между телами нет и нет никакого посредника для передачи кинетической энергии, следовательно нет соударений между микрочастицами тел и Q = 0.
Рис. 37. Модель обмена энергией в форме теплоты (соударения микрочастиц) горячего (система 1) и холодного (система 2) тел Несложно вычислить теплоту Q, которая необходима для нагревания тела от температуры Т 1 до температуры Т 2 Для этого необходимо иметь сведения о средней теплоемкости тела. Средняя теплоемкость С – это количество энергии в форме теплоты, затраченное на нагревание одного моля или одного грамма вещества на 1 К. Из определения следует
Теплоемкость Запишем уравнение первого закона термодинамики для бесконечно малого изменения состояния системы dQ = dU + dА (4.9) dU является функцией состояния, а dQ и dА не являются функциями состояния системы. Они являются характеристиками процесса. Если нет процесса, то работа и теплота равны нулю. В термодинамике большую роль играют круговые процессы - циклы. В двигателе внутреннего сгорания, в паровой машине совершаются такие циклы, позволяющие получить работу в тепловом процессе сжигания топлива. Если единственной работой является работа расширения идеального газа, вычисляемая по уравнению dA = p dV, (4.10) то уравнение первого закона термодинамики примет вид dQ = dU + рdV. (4.11) Введем понятие истинная теплоемкость при постоянном объеме и постоянном давлении. При постоянном объеме (V = const) dV =0 и dQV = dU, (4.12) и мы получим выражение теплоемкости при постоянном объеме
Запишем уравнение первого закона термодинамики при р = const dQp = dU + рdV (4.14) dQp = d(U + рV) dQp = dН, (4.15) где H – энтальпия химической реакции H = (U +pV). Из уравнения (4.15) выражение теплоемкости при постоянном давлении
Отметим, что единственный случай, когда теплота физико-химического процесса является функцией состояния, то есть определяется начальным и конечным состояниями системы, отражена в уравнениях (4.12) и (4.15). Величины удельной и мольной теплоемкости индивидуальных соединений имеют размерности [Дж/г×К] и [Дж/моль×К] соответственно. Между мольными теплоемкостями идеального газа при постоянном давлении и объеме существует связь. Её можно получить из уравнения (4.16):
Поскольку внутренняя энергия идеального газа не зависит от давления и объема,
Используя уравнение состояния идеального газа, найдем, что Ср = СV + R. (4.17) Газовая постоянная R = 8.314 Дж/моль К имеет ту же размерность, что и мольная теплоемкость.
Пример. Вычислим количество энергии, которое необходимо для нагревания 1 г воды (Ср = 4.18 Дж/г К) и 1 г железа (Ср = 0.448 Дж/г К) – от 25 до 100 0С.
Решение dQ = Ср × dT
Q = Ср (Т 2 – Т 1) Q (Н2О) = 4.18 (373 – 298) = 313.5 [Дж/г×К] Q (Fe) = 0.448 (373 – 298) = 33.6 [Дж/г×К]. Не случайно в жаркий солнечный день одинаковые по площади и массе водные и металлические поверхности по-разному нагреваются.
Работа Работа А – это форма обмена энергией системы с окружающей средой посредством направленного движения макросистемы как целого. Например, газ в цилиндре под поршнем расширяется и совершает работу, поднимает груз на некоторую высоту. (рис. 35). Работа совершается за счет энергии нагревателя, передаваемой в форме теплоты. Газ совершает направленное движение, перемещая поршень с грузом, поэтому работа является макрофизической формой обмена энергией системы и окружающей среды. Рассмотрим работу расширения (или сжатия), совершаемую идеальным газом. Работа изобарного расширения (р = const) Работа изобарного расширения n моль идеального газа (работа подъема груза на некоторую высоту) осуществляется за счет внешнего источника энергии (нагревателя) в соответствии с уравнением dQр = dU + рdV. Газ, находящийся в цилиндре под поршнем, изменяет внутреннюю энергию (нагревается) и совершает работу. При р = const нагревание газа сопровождается изменением объема от V 1 до V 2. Модель такого процесса представлена на рис. 35. Интегрируем уравнение dA = p dV
А = р (V 2 – V 1). (4.18) Графически в координатах р – V работа изобарного расширения представлена площадью (рис. 38).
Рис. 38. Работа изобарного расширения
Для n моль исходное и конечное состояния идеального газа выражаются уравнениями. PV 1 = nRT 1 и PV 2 = nRT 2. Заменим объемы в уравнении (4.18), тогда
Из уравнений (4.18) и (4.19) следует, что работа расширения идеального газа при постоянном давлении есть функция состояния. Она определяется только начальным и конечным состояниями системы. В данном случае начальное и конечное состояния определяются значениями V и T. Работа изотермического расширения (Т = const) Работа изотермического расширения n моль идеального газа также осуществляется за счет внешнего источника энергии (нагревателя, или термостата), но при этом изменяется давление в системе так, как это представлено на рис. 39. Внутренняя энергия идеального газа является функцией температуры. При Т = const dU = 0, и уравнение первого закона термодинамики принимает вид:
dQ = рdV
Рис. 39. Расширение газа по мере уменьшения груза (количества песчинок) на поршне: а) исходное состояние; б) конечное состояние системы
Интегрируем уравнение dA = p dV
Графически в координатах р – V работа изотермического расширения представлена площадью, показанной на рис. 40.
Рис. 40. Работа изотермического расширения
Работа адиабатического расширения (dQ = 0) В адиабатическом процессе система обменивается с окружающей средой энергией только в форме работы (dQ = 0), поэтому работа адиабатического расширения осуществляется за счет внутренней энергии n моль идеального газа (рис. 41).
Рис. 41. Адиабатическое расширение (сжатие) идеального газа
При dQ = const уравнение первого закона термодинамики принимает вид: 0= dU + dА. Так как работа расширения в адиабатическом процессе происходит за счет уменьшения внутренней энергии системы, то при расширении газ охлаждается, при сжатии – разогревается. Из уравнения (4.13) dU =n CVdT, тогда dА = - nCVdT
А =nСV (Т 1 – Т 2) (4.21) В координатах p – V уравнения изотермы и адиабаты имеют вид рV = const и
Рис. 42. Работа адиабатического расширения (закрашенная область) меньше, чем работа изотермического расширения в одной и той же области изменений давления
Для изохорного процесса (V = const) работа расширения равна А = 0.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.255.63 (0.011 с.) |

 связывает свойства таким образом, что любое из них можно определить, если известны другие.
связывает свойства таким образом, что любое из них можно определить, если известны другие. и
и 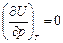 .
. . (4.7)
. (4.7)
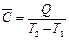 или Q =
или Q = 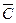 (T 2 – Т 1)
(T 2 – Т 1) . (4.13)
. (4.13) . (4.16)
. (4.16) .
.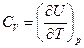 и
и  .
. , тогда
, тогда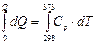


 . (4.19)
. (4.19)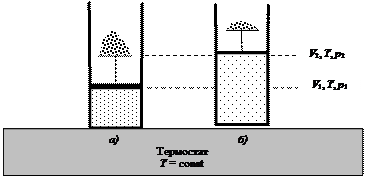

 (4.20)
(4.20)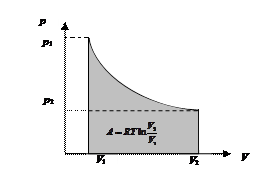


 const соответственно, где
const соответственно, где  . Графически в координатах р – V работа адиабатического расширения представлена площадью, изображенной на рис. 42.
. Графически в координатах р – V работа адиабатического расширения представлена площадью, изображенной на рис. 42.



