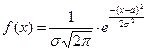Закон распределение вероятностей дискретной случайной величины

Закон распределение вероятностей дискретной случайной величины

Законом распределения случайной величины называется любое со­отношение, связывающее возможные значения этой случайной ве­личины и соответствующие им вероятности. Закон распределения дискретной случайной величины задается чаще всего не функцией распределения, а рядом распределения, т.е, таблицей

В которой x1, x2,..., xn,... - расположенные по возрастанию значения дискретной случайной величины X, а р1, р₂,..., р_п,... — отвечающие этим значениям вероятности: p_i = Р{Х = хi), i= 1, 2,..., п,.... Число столбцов в этой таблице может быть конечным (если соответствующая случайная величина принимает конечное число значений) или бесконечным,S pi= 1.

Многоугольником распределения дискретной случайной величины X называется ломаная, соединяющая точки {xi; pi), расположенные в Порядке возрастания хi. – это графический способ – полигон распределения вероятностей.

Математические операции над ДСВ

1.Произведение к на х называется случайная величина, которая принимает значение кхi с теми же самыми вероятностями.

2.Возведение случайной величины в степень: m-ой степенью СВ х называется СВ, которая принимает значение хim c теми же самыми вероятностями.

3.Суммой (разностью, произведением) СВ Х и Y называется СВ, которая принимает все возможные значения типа

хi+yj (xi-yj; xiyj) с вероятностями того, что СВ Х принимает значение хi, а СВ Y принимает значение уj, т.е.

р - вероятность того, что Р(Х=хi и Y=уj) равны произведению вероятностей событий: р(Х=хi)*p(Y=yj)

Эти события независимы X и Y.

Математическое ожидание ДСВ. Математическое ожидание числа появления событий в n независимых испытаниях.

Мат. Ожиданием Д.С.В. называют сумму произведений всех ее возможных значений на их вероятности: М(Х)=х1р1+х2р2+…+хnpn. Мат. ожидание обладает следующими свойствами: 1) Мат. ожидание постоянной величины равно самой постоянной: М(С)=С. 2) Постоянный множитель можно выносить за знак мат. ожидания: М (СХ)=СМ (Х). 3) Мат. ожидание произведения взаимно независимых С.В. равно произведению мат. ожиданий сомножителей: М (Х1,Х2…Хn)=M(X1)*M(X2)…M(Xn). 4) Мат. ожидание суммы (разности) С.В. равно сумме(разности) мат. ожиданий слагаемых:

М (Х1+Х2+Х3+…+Хn)=M(X1)+M(X2)+M(X3)+…+M(Xn).

Мат ожидание числа появления событий в н независимых испытаниях равна произведению числа испытаний на р, где р – это вероятность появления события в каждом испытании, то есть М(Х) = n *р, где р = Р (А), Х – число появления события А в н независимых испытаниях предстваляется в виде суммы отдельных случайных величин Х итое, то есть Х = сумме Х итых, где Х-итое – это появление события А в итом испытании. Х1-число появлений события А в 1-м испытании.

Х2-число появлений события А во 2-м испытании.

Хn-число появлений события А в n испытании.

Х= Х1+Х2+…+Хn

1 – либо происходит в испытании либо нет М(Хi) = сумма хi*pi = 1p+0(1-p) = p

X = сумма Хi, M(X) = M (сумма Хi) = сумма M (Xi) = np

16. Дисперсия ДСВ. Дисперсия появления числа событий в n независимых испытаниях. Дисперсией D(X) СВ называют матем. ожидание квадрата ее отклонения от мат. ожидания, т.е. D(X)=M(X-M(X))2. Основн. св-ва дисперсии:

1) Дисперс. алгебраич. Суммы (разность) 2-ух независим. СВ X и Y равна сумме дисперсий этих величин, т.е. D(X+или- Y)=D(X)+D(Y

2) Дисперсия постоян. величины равна 0, т.е. D(C)=0. Доказ-во: Т.к. M(C)=C, то D(C)= M(C – M(C))2 = M(C – C)2 = M(0) = 0;

3) Постоян. множитель С можно выносить за знак дисперсии, возводя его в квадрат, т.е. D(CX)= C в квадрате*D(X).

4) Дисперсия СВ Х равна разности между мат. ожиданием квадрата СВ и квадратом ее мат. ожидания, т.е. D(X) = M(X2) – (M(X))2.

Дисперсия числа появлений события в n независимых испытаниях

Эксперимент повторяется n раз, А- событие.

Р(А)=р

Р(неА)=q=1-p

X-число появлений события А в n-независимых испытаниях.

М(Х)=np

Дисперсия числа появления события n-независимых испытаний равно npq.

D(X)=npq, где р- вероятность появления события;р=Р(А);q=Р(неА)

D (Xi) = M (Xi в квадрате) – (M (X)) в квадрате = p – p в квадрате = p (1-p) = p*q

Хi 0 1

P q p

D(X)=D(X1)+D(X2)+…+D(Xn) = npq

Вероятность отдельно взятого значения НСВ. Вероятность попадания НСВ в заданный интервал.

Теорема: Вероятность любого отдельно взятого значения НСВ равна нулю. Поэтому НСВ можно определить как: случайная величина непрерывна, если вероятность любого отдельно взятого ее значения равна нулю.

Вероятность попадания НСВ в заданный интервал

Вер. попадания СВ Х в задан. Интервал [а;в] равна определенному интегралу от ее плотности вероятности в пределах от а до в, то есть Р (а меньше или равно Х меньше или равно в) = интеграл от а до в фи (х)dx = F(в) – F(а)

При этом плотность вероятности неотрицательная функция, то есть фи(х) больше или равно 0.

Наиболее часто встречаемые законы распределения ДСВ.

Биномиальным закон распределения Д.С.В. ДСВ распределятеся по этому закону с параметрами n и р, если мн-во ее значений совпадает со мн-ом целых неотрицательных чисел от 0 до n, а соответствующие им вероятности рассчитываются по формуле Бернулли Pn (k)=Cn^k* p^k *q^(n-k), при этом М(Х) = np, D(x) = npq

Наиболее часто встречаемые законы распределения вероятностей НСВ.

Нормальный закон распределения НСВ

НСВ имеет Нормальный закон распределения с параметрами а и сигма в квадрате задается плотностью распределения вида

Закон распределение вероятностей дискретной случайной величины

Законом распределения случайной величины называется любое со­отношение, связывающее возможные значения этой случайной ве­личины и соответствующие им вероятности. Закон распределения дискретной случайной величины задается чаще всего не функцией распределения, а рядом распределения, т.е, таблицей

В которой x1, x2,..., xn,... - расположенные по возрастанию значения дискретной случайной величины X, а р1, р₂,..., р_п,... — отвечающие этим значениям вероятности: p_i = Р{Х = хi), i= 1, 2,..., п,.... Число столбцов в этой таблице может быть конечным (если соответствующая случайная величина принимает конечное число значений) или бесконечным,S pi= 1.

Многоугольником распределения дискретной случайной величины X называется ломаная, соединяющая точки {xi; pi), расположенные в Порядке возрастания хi. – это графический способ – полигон распределения вероятностей.

Познавательные статьи:



Организация работы процедурного кабинета

Статус республик в составе РФ

Понятие финансов, их функции и особенности

Сущность демографической политии