
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика проведения экспериментаСодержание книги
Поиск на нашем сайте
И ОБРАБОТКИ РЕЗУЛЬТАТОВ Лабораторное оборудование: · токарно-винторезный станок; · заготовка; · резец токарный проходной с пластинкой из твердого сплава; · динамометр. Перед началом работы следует ознакомиться с оборудованием и приборами; убедиться в тщательности закрепления динамометра, обрабатываемой заготовки и инструмента на станке, так как в противном случае возникают вибрации, искажающие результаты опытов. Вылет резца в державке динамометра должен соответствовать условиям тарировки. Динамометр устанавливают на суппорте токарного станка таким образом, чтобы вершина резца находилась на линии центров станка. При установлении силовых зависимостей используют однофакторный эксперимент, который, являясь более трудоемким, в то же время обеспечивает высокую точность. В случае однофакторного эксперимента варьируют только тот фактор процесса резания, влияние которого изучают, а все остальные факторы за время опыта остаются неизменными. Конечной целью эксперимента является установление функциональной связи между независимой переменной, в качестве которой выступают характеристики процесса резания, и зависимой переменной, которой является составляющая силы резания, и описание этой связи математической эмпирической формулой. Точность получаемых результатов при однофакторном эксперименте главным образом зависит от постоянства факторов, не учитываемых в данной серии опытов. Результаты наблюдений при невысокой стабильности условий проведения и метрологического оснащения необходимо подвергать статистическому анализу: определение погрешности измерений, установление доверительного интервала, оценка воспроизводимости результатов отдельных опытов. В настоящей лабораторной работе проводится три серии опытов. В первой серии определяется зависимость главной составляющей силы резания от глубины резания при прочих неизменных условиях. Вторая серия опытов устанавливает зависимость главной составляющей силы резания от подачи. В третьей серии определяется зависимость главной составляющей силы резания от скорости при остальных постоянных параметрах. Частоту вращения заготовки подсчитывают по формуле:
где D – диаметр обрабатываемой поверхности заготовки, мм.
Затем подбирается ближайшая имеющаяся на станке частота вращения шпинделя, и подсчитывается скорость резания, осуществляемая в опытах. Для каждого принятого в опытах сочетания значений скорости, подачи и глубины резания регистрируют показания динамометра и заносят в протокол отчета (табл. 1). Таблица 1 Протокол измерений
Сила резания определяется по тарировочному графику (см. рис. 3) соответственно показаниям динамометра. В работе используется механический однокомпонентный динамометр (рис. 4). Динамометр устанавливают на верхних салазках суппорта токарного станка вместо предварительно снятого резцедержателя и закрепляют болтом, проходящим через отверстие А. Резец закрепляется в державке 3, которая соединена с корпусом динамометра 1 посредством двух упругих торсионных брусков 2 квадратного сечения. Под действием составляющей силы резания PZ резец отжимается вниз, упруго скручивая торсионные бруски. При этом находящийся в нижней части прибора свободный конец планки 4, приваренный другим концом к державке 3, поднимается, нажимая посредством стержня 6 на ножку индикатора 5. Ножка индикатора перемещается пропорционально упругой деформации торсионных брусков и, следовательно, главной составляющей силы резания. Для устранения влияния неизбежных колебаний планки 4 и ножки индикатора предусмотрено простое демпфирующее устройство, включающее насаженный на стержень 6 поршень 7 с двумя малыми отверстиями, помещенный в закрытый, заполненный вязким маслом цилиндр в корпусе динамометра.
Рис. 4. Схема однокомпонентного токарного динамометра В каждом опыте из-за наличия случайных погрешностей наблюдается разброс выходных значений силы резания. Для оценки дисперсии воспроизводимости используют критерий Кохрена. Для каждой опытной точки дисперсия подсчитывается по формуле:
где n – число дублей; уji – значение функции i -го дубля в j-м опыте;
Критерий Кохрена G представляет собой отклонение наибольшей дисперсии, полученной в опытах, к сумме дисперсий всех опытов:
где N – число опытов (измеряемых точек). Если G > GКРИТ, то это означает, что в одном или нескольких опытах рассеяние результатов вследствие неучтенных факторов или случайных ошибок, слишком велико и опыты необходимо повторить. Значения GКРИТ приведены в табл. 2 в зависимости от доверительной вероятности р и числа степеней свободы q = n – 1. Таблица 2 Критерий Кохрена G при р = 0,95
Проверку адекватности модели производят с помощью критерия Фишера, представляющего собой отношение дисперсии адекватности
Критерий Фишера обычно применяют для определения адекватности малых выборок, в больших выборках целесообразно применять критерии Пирсона, Романовского, Колмогорова. Дисперсия адекватности определяется по формуле:
где n – число повторов в каждой точке; уj – среднее значение отклика в j-й точке;
N – количество различных точек; d – количество коэффициентов в уравнении регрессии. Средняя дисперсия для оценки дисперсии воспроизводимости:
Вычисленный критерий сравнивают с критическим FКРИТ. Если F > FКРИТ, то модель адекватна функции отклика. В противном случае модель должна быть изменена [5]. Значение FКРИТ принимают по табл. 3 для определенной доверительной вероятности и числа степеней свободы q1 = n – d, q2 = n ×(N – 1). Таблица 3 Критерий Фишера F для р = 0,95
Полученные экспериментальные данные обрабатывают для получения формулы, отражающей связь параметров процесса резания с соответствующей им силой резания. Зависимость главной составляющей силы резания PZ от глубины резания, отражающая содержание первой серии экспериментов, может быть описана уравнением вида: PZ = CX × t Xp, (1) от подачи, в соответствии со второй серией экспериментов: PZ = CY × S Yp, (2) и от скорости, по третьей серии экспериментов: PZ = CZ × V Zp. (3) Эти уравнения называются частными эмпирическими. В результате обработки экспериментальных данных требуется найти параметры общей эмпирической зависимости вида:
PZ = CpZ × t Xp× S Yp× V Zp, (4)
показатели степени в котором xР: yР; zР равны соответствующим показателями в частных уравнениях, а коэффициент CpZ этого уравнения не совпадает ни с одним из CХ , CY или CZ. Прологарифмировав одно из частных уравнений, например (1), получим
Введем для наглядности временное переобозначение lgPZ = y; lgCХ = a; xР= b; lg t = x и перепишем уравнение (5):
у = а + b × х. (6)
Полученное уравнение (6) является уравнением прямой линии с угловым коэффициентом b в декартовых координатах с функциональными логарифмическими шкалами. Такого же вида уравнения могут быть получены после применения аналогичных преобразований к другим частным уравнениям.
В науке о резании металлов используют различные методы обработки экспериментальных данных. Наибольшее применение получили графоаналитический и метод наименьших квадратов. Сущность графоаналитического метода заключается в том, что неизвестные параметры искомого уравнения определяются графическим путем. При этом по экспериментальным точкам проводят прямую, наилучшим образом соответствующую функциональной зависимости, и затем определяют ее параметры. 1. Построение наилучшей прямой с помощью линейки (рис.5,а). Наложив на график с экспериментальными точками прозрачную линейку, находим такое положение, при котором экспериментальные точки достаточно плотно лежат вдоль нее, и проводим прямую. 2. Метод парных точек (рис.5,б). Соединяем попарно точки и определяем несколько значений тангенса угла наклона. В качестве наилучшего принимаем среднее значение. Прямую в этом случае проводят через точку, имеющую в качестве координат средние значения абсциссы и ординаты. Метод дает удовлетворительные результаты, если разность ординат попарных точек примерно равны.
а б Рис. 5. Графоаналитический метод построения наилучшей прямой Коэффициент b уравнения (6) (показатель степени в уравнениях (1)…(4)) есть тангенс угла наклона прямой к оси абсцисс:
Определить коэффициенты CХ или CY можно по графику, пользуясь свойством степенной функции 11=1, то есть значение постоянной CХ или CY равно тому значению зависимой переменной, которое она принимает при единичном значении независимой. Если единичное значение независимой переменной отсутствует в перечне экспериментальных данных, то график экстраполируют до единичного значения. Если это является затруднительным, например, единичное значение независимой переменной далеко отстоит от экспериментального диапазона, то определить коэффициент можно аналитически и например, для скорости резания коэффициент CZ из формулы (3):
Расчет постоянной по этой формуле производится для всех опытов из серии, в данном случае 4 раза и окончательно принимается среднее арифметическое из них. При методе наименьших квадратов параметры искомого уравнения находят расчетным путем. Находится кривая, для которой сумма квадратов разности значений функции и экспериментальных точек минимальна. Для нашего случая условие имеет вид:
где xi, yi – абсцисса и ордината i -й экспериментальной точки; n – число экспериментальных точек. Для расчета коэффициентов a и b уравнений вида (6) имеются следующие формулы:
После определения коэффициентов и показателей степеней частных зависимостей (1)…(3) необходимо найти коэффициент СРz общей зависимости (4). Исходной посылкой является то, что при определении частных зависимостей во всех случаях эксперименты имели одну общую точку с координатами (t0; S0; V0). Тогда в этой точке величину PZ можно рассчитать как по общей, так и по частным зависимостям: PZ = CpZ × t Xp× S Yp× V Zp = CХ × t Xp = CY × S Yp = CZ × V Zp.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.109.152 (0.011 с.) |

 ,
,
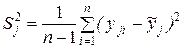 ,
, – среднее значение j-го опыта.
– среднее значение j-го опыта. ,
,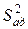 к средней дисперсии опыта S 2:
к средней дисперсии опыта S 2: .
. ,
, – вычисленное по уравнению регрессии значение отклика в j-й точке;
– вычисленное по уравнению регрессии значение отклика в j-й точке; .
. (5)
(5)
 .
. .
.  ,
,
 .
.


