
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование силы резания при точенииСодержание книги
Поиск на нашем сайте
ИССЛЕДОВАНИЕ СИЛЫ РЕЗАНИЯ ПРИ ТОЧЕНИИ
Методические указания к лабораторной работе по курсу «Операции и процессы формообразования» для студентов направления КТОП
Одобрено редакционно-издательским советом Саратовского государственного технического университета Саратов 2013 Цель работы: исследование влияния элементов режима резания (скорости, подачи и глубины резания) на главную составляющую силы резания при точении, а также приобретение навыков обработки экспериментальных данных для получения эмпирических зависимостей.
ОСНОВНЫЕ ПОНЯТИЯ
Срезаемый слой давит на резец с силой резания Р, являющейся геометрической суммой нормальных сил и сил трения, действующих на передней и задней поверхностях. В общем случае сила резания не расположена в главной секущей плоскости, а составляет с ней некоторый угол. При изменении обрабатываемого материала, геометрических параметров резца и режимов резания сила Р меняет как свою величину, так и направление в пространстве. Поэтому при расчетах силу резания проектируют на оси некоторой стабильно расположенной при резании системы координат X, Y, Z, ось Z которой совпадает по направлению с вектором скорости главного движения, оси X – противоположно направлению подачи, а направление оси Y соответствует правой системе координат (рис. 1). Полученные при этом составляющие называют: РX – осевая (сила подачи), PY – радиальная и PZ – тангенциальная (главная). Зная величины составляющих, легко определить величину силы резания:
Рис. 1. Сила резания при продольном точении Главная составляющая силы резания PZ действует на резец, изгибая его в вертикальной плоскости, а ее реакция также в вертикальной плоскости изгибает деталь. Эффективную мощность станка рассчитывают только по силе PZ. Радиальная составляющая силы резания PY стремится оттолкнуть резец от детали, а ее реакция изгибает деталь в горизонтальной плоскости. Осевая составляющая силы резания РX противодействует продвижению суппорта станка вдоль оси детали. По ее величине рассчитывают на прочность механизм подачи станка. Сила РX изгибает резец в горизонтальной плоскости, а ее реакция сдвигает деталь вдоль оси.
Силы РX, PY и PZ в общем случае неодинаковы. Величина силы PZ главным образом определяется нормальной силой, действующей на передней поверхности резца. Силы РX и PY зависят от величины и направления силы трения. Соотношения между составляющими силы резания меняются в зависимости от обрабатываемого материала, геометрических параметров резца и режимов резания. При достаточно употребительных характеристиках инструмента: j = 45°, l = 0, g = 15° и отношении t/s > 10 – приближенно выполняются следующие соотношения: PZ: PY: РX = 1: (0,4…0,5): (0,25…0,3), при этом главная составляющая PZ мало отличается от силы резания (на 10-15%). При увеличении глубины резания и подачи растет площадь сечения срезаемого слоя, что вызывает возрастание всех составляющих силы резания. Однако результаты экспериментов, проведенных при точении различных материалов с прямыми срезаемыми слоями, свидетельствуют, что во всех случаях глубина резания на силу резания влияет сильнее, нежели подача. Известно, что изменение ширины срезаемого слоя b не сказывается на изменении степени его деформации (коэффициент усадки стружки остается постоянным). Увеличение же толщины срезаемого слоя а снижает величину коэффициента усадки стружки. Главная составляющая силы резания пропорциональна той степени деформации, которую получил срезаемый слой при превращении его в стружку. При увеличении ширины срезаемого слоя вследствие увеличения площади сечения сила PZ увеличивается во столько раз, во сколько возросла величина b. При увеличении толщины срезаемого слоя также увеличивается его площадь, но при этом степень деформации слоя уменьшается и рост силы PZ отстает от роста а. Поскольку физические и технологические размеры срезаемого слоя связаны друг с другом только через главный угол в плане, то влияние t и S на силу PZ остается таким же, как влияние b и а.
Изменение скорости резания влияет на силу резания так, как оно влияет на изменение коэффициента усадки стружки. При резании материалов, не склонных к образованию нароста, коэффициент усадки монотонно убывает при увеличении скорости резания. Так же ведет себя и главная составляющая силы резания. При резании материалов, склонных к наростообразованию, кривые PZ =f (V) и K =f (V) немонотонны (рис. 2), причем обе кривые совпадают по фазам. Начиная от скорости V1 до скорости V2, при которых высота нароста растет, сила PZ уменьшается, достигая минимума при максимально развитом наросте. При скоростях резания от V2 до V3 сила PZ вновь возрастает. При скоростях резания, больше V 3, соответствующей исчезновению нароста, сила PZ непрерывно уменьшается и при V > 400 м/мин практически перестает влиять.
Знание сил, действующих в процессе резания, необходимо для расчета и конструирования режущего инструмента, станков и приспособлений, а также для расчета жесткости технологической системы и определения мощности, затрачиваемой на резание. Связь между изменением факторов процесса резания и составляющими силы резания обычно находят экспериментально в виде эмпирической формулы. Аналитические методы определения составляющих силы резания имеют преимущественно теоретический характер и для инженерных расчетов не применяются. Приборы, предназначенные для измерения силы резания, называют динамометрами. Если динамометр измеряет одну составляющую, то его называют однокомпонентным, иначе – многокомпонентным. По принципу действия различают механические, гидравлические и электрические (индуктивные, емкостные, тензометрические). Независимо от конструкции динамометры состоят из трех основных частей: 1) датчика, являющегося основой для определения величины силы резания; он воспринимает нагрузку, перемещения, связанные с упругой деформацией датчика, или изменения параметров электрической цепи, связанные с упругой деформацией; 2) приемника, регистрирующего выходной параметр датчика; 3) вспомогательных звеньев, связывающих датчик и приемник. К динамометрам предъявляют следующие основные требования: · при измерении не сообщать резцу или шпинделю дополнительные перемещения, не изменять жесткость системы, быть виброустойчивым; · иметь малую инерционность, для чего собственная частота колебаний динамометра должна быть в несколько раз больше частоты колебаний измеряемой силы; · в многокомпонентном динамометре должно отсутствовать взаимное влияние составляющих силы резания (датчик, воспринимающий действие одной из составляющих силы резания, не должен реагировать на действие других составляющих); · точность измерения сил резания должна составлять 1…2 % при исследовании физических процессов, 2…3 % при определении мощности, расчетах на жесткость и прочность.
Динамометры не позволяют определить непосредственно величины сил резания – их показания дают значения, пропорциональные действующей силе. Поэтому перед работой необходимо протарировать динамометр. Тарирование заключается в том, что динамометр нагружают в направлении силы резания сначала возрастающим, а затем убывающими силами, величина которых известна. Показания динамометра, соответствующие определенным величинам сил, регистрируются. На основании этих данных по средней линии нагрузки и разгрузки строится тарировочный график (рис. 3), который в дальнейшем используют для расшифровки показаний динамометра. Конструкция механического динамометра основана на том, что тонкая стенка, несущая на себе резцедержатель с резцом, под действием сил резания упруго деформируется. Перемещения, появляющиеся в результате этой деформации, регистрируются индикаторами. По этим перемещениям можно судить о величине действующих сил. Они просты по конструкции, но весьма чувствительны к вибрациям и сами могут вызвать ее, обладают значительной инерционностью. Стрелка индикатора, регистрирующая перемещение, сильно колеблется, что затрудняет замеры и отсчет, а также записи изменения величин.
И ОБРАБОТКИ РЕЗУЛЬТАТОВ Лабораторное оборудование: · токарно-винторезный станок; · заготовка; · резец токарный проходной с пластинкой из твердого сплава; · динамометр. Перед началом работы следует ознакомиться с оборудованием и приборами; убедиться в тщательности закрепления динамометра, обрабатываемой заготовки и инструмента на станке, так как в противном случае возникают вибрации, искажающие результаты опытов. Вылет резца в державке динамометра должен соответствовать условиям тарировки. Динамометр устанавливают на суппорте токарного станка таким образом, чтобы вершина резца находилась на линии центров станка. При установлении силовых зависимостей используют однофакторный эксперимент, который, являясь более трудоемким, в то же время обеспечивает высокую точность. В случае однофакторного эксперимента варьируют только тот фактор процесса резания, влияние которого изучают, а все остальные факторы за время опыта остаются неизменными. Конечной целью эксперимента является установление функциональной связи между независимой переменной, в качестве которой выступают характеристики процесса резания, и зависимой переменной, которой является составляющая силы резания, и описание этой связи математической эмпирической формулой. Точность получаемых результатов при однофакторном эксперименте главным образом зависит от постоянства факторов, не учитываемых в данной серии опытов. Результаты наблюдений при невысокой стабильности условий проведения и метрологического оснащения необходимо подвергать статистическому анализу: определение погрешности измерений, установление доверительного интервала, оценка воспроизводимости результатов отдельных опытов. В настоящей лабораторной работе проводится три серии опытов. В первой серии определяется зависимость главной составляющей силы резания от глубины резания при прочих неизменных условиях. Вторая серия опытов устанавливает зависимость главной составляющей силы резания от подачи. В третьей серии определяется зависимость главной составляющей силы резания от скорости при остальных постоянных параметрах.
Частоту вращения заготовки подсчитывают по формуле:
где D – диаметр обрабатываемой поверхности заготовки, мм. Затем подбирается ближайшая имеющаяся на станке частота вращения шпинделя, и подсчитывается скорость резания, осуществляемая в опытах. Для каждого принятого в опытах сочетания значений скорости, подачи и глубины резания регистрируют показания динамометра и заносят в протокол отчета (табл. 1). Таблица 1 Протокол измерений
Сила резания определяется по тарировочному графику (см. рис. 3) соответственно показаниям динамометра. В работе используется механический однокомпонентный динамометр (рис. 4). Динамометр устанавливают на верхних салазках суппорта токарного станка вместо предварительно снятого резцедержателя и закрепляют болтом, проходящим через отверстие А. Резец закрепляется в державке 3, которая соединена с корпусом динамометра 1 посредством двух упругих торсионных брусков 2 квадратного сечения. Под действием составляющей силы резания PZ резец отжимается вниз, упруго скручивая торсионные бруски. При этом находящийся в нижней части прибора свободный конец планки 4, приваренный другим концом к державке 3, поднимается, нажимая посредством стержня 6 на ножку индикатора 5. Ножка индикатора перемещается пропорционально упругой деформации торсионных брусков и, следовательно, главной составляющей силы резания. Для устранения влияния неизбежных колебаний планки 4 и ножки индикатора предусмотрено простое демпфирующее устройство, включающее насаженный на стержень 6 поршень 7 с двумя малыми отверстиями, помещенный в закрытый, заполненный вязким маслом цилиндр в корпусе динамометра.
Рис. 4. Схема однокомпонентного токарного динамометра В каждом опыте из-за наличия случайных погрешностей наблюдается разброс выходных значений силы резания. Для оценки дисперсии воспроизводимости используют критерий Кохрена. Для каждой опытной точки дисперсия подсчитывается по формуле:
где n – число дублей; уji – значение функции i -го дубля в j-м опыте;
Критерий Кохрена G представляет собой отклонение наибольшей дисперсии, полученной в опытах, к сумме дисперсий всех опытов:
где N – число опытов (измеряемых точек). Если G > GКРИТ, то это означает, что в одном или нескольких опытах рассеяние результатов вследствие неучтенных факторов или случайных ошибок, слишком велико и опыты необходимо повторить. Значения GКРИТ приведены в табл. 2 в зависимости от доверительной вероятности р и числа степеней свободы q = n – 1.
Таблица 2 Критерий Кохрена G при р = 0,95
Проверку адекватности модели производят с помощью критерия Фишера, представляющего собой отношение дисперсии адекватности
Критерий Фишера обычно применяют для определения адекватности малых выборок, в больших выборках целесообразно применять критерии Пирсона, Романовского, Колмогорова. Дисперсия адекватности определяется по формуле:
где n – число повторов в каждой точке; уj – среднее значение отклика в j-й точке;
N – количество различных точек; d – количество коэффициентов в уравнении регрессии. Средняя дисперсия для оценки дисперсии воспроизводимости:
Вычисленный критерий сравнивают с критическим FКРИТ. Если F > FКРИТ, то модель адекватна функции отклика. В противном случае модель должна быть изменена [5]. Значение FКРИТ принимают по табл. 3 для определенной доверительной вероятности и числа степеней свободы q1 = n – d, q2 = n ×(N – 1). Таблица 3 Критерий Фишера F для р = 0,95
Полученные экспериментальные данные обрабатывают для получения формулы, отражающей связь параметров процесса резания с соответствующей им силой резания. Зависимость главной составляющей силы резания PZ от глубины резания, отражающая содержание первой серии экспериментов, может быть описана уравнением вида: PZ = CX × t Xp, (1) от подачи, в соответствии со второй серией экспериментов: PZ = CY × S Yp, (2) и от скорости, по третьей серии экспериментов: PZ = CZ × V Zp. (3) Эти уравнения называются частными эмпирическими. В результате обработки экспериментальных данных требуется найти параметры общей эмпирической зависимости вида:
PZ = CpZ × t Xp× S Yp× V Zp, (4)
показатели степени в котором xР: yР; zР равны соответствующим показателями в частных уравнениях, а коэффициент CpZ этого уравнения не совпадает ни с одним из CХ , CY или CZ. Прологарифмировав одно из частных уравнений, например (1), получим
Введем для наглядности временное переобозначение lgPZ = y; lgCХ = a; xР= b; lg t = x и перепишем уравнение (5):
у = а + b × х. (6)
Полученное уравнение (6) является уравнением прямой линии с угловым коэффициентом b в декартовых координатах с функциональными логарифмическими шкалами. Такого же вида уравнения могут быть получены после применения аналогичных преобразований к другим частным уравнениям. В науке о резании металлов используют различные методы обработки экспериментальных данных. Наибольшее применение получили графоаналитический и метод наименьших квадратов. Сущность графоаналитического метода заключается в том, что неизвестные параметры искомого уравнения определяются графическим путем. При этом по экспериментальным точкам проводят прямую, наилучшим образом соответствующую функциональной зависимости, и затем определяют ее параметры. 1. Построение наилучшей прямой с помощью линейки (рис.5,а). Наложив на график с экспериментальными точками прозрачную линейку, находим такое положение, при котором экспериментальные точки достаточно плотно лежат вдоль нее, и проводим прямую. 2. Метод парных точек (рис.5,б). Соединяем попарно точки и определяем несколько значений тангенса угла наклона. В качестве наилучшего принимаем среднее значение. Прямую в этом случае проводят через точку, имеющую в качестве координат средние значения абсциссы и ординаты. Метод дает удовлетворительные результаты, если разность ординат попарных точек примерно равны.
а б Рис. 5. Графоаналитический метод построения наилучшей прямой Коэффициент b уравнения (6) (показатель степени в уравнениях (1)…(4)) есть тангенс угла наклона прямой к оси абсцисс:
Определить коэффициенты CХ или CY можно по графику, пользуясь свойством степенной функции 11=1, то есть значение постоянной CХ или CY равно тому значению зависимой переменной, которое она принимает при единичном значении независимой. Если единичное значение независимой переменной отсутствует в перечне экспериментальных данных, то график экстраполируют до единичного значения. Если это является затруднительным, например, единичное значение независимой переменной далеко отстоит от экспериментального диапазона, то определить коэффициент можно аналитически и например, для скорости резания коэффициент CZ из формулы (3):
Расчет постоянной по этой формуле производится для всех опытов из серии, в данном случае 4 раза и окончательно принимается среднее арифметическое из них. При методе наименьших квадратов параметры искомого уравнения находят расчетным путем. Находится кривая, для которой сумма квадратов разности значений функции и экспериментальных точек минимальна. Для нашего случая условие имеет вид:
где xi, yi – абсцисса и ордината i -й экспериментальной точки; n – число экспериментальных точек. Для расчета коэффициентов a и b уравнений вида (6) имеются следующие формулы:
После определения коэффициентов и показателей степеней частных зависимостей (1)…(3) необходимо найти коэффициент СРz общей зависимости (4). Исходной посылкой является то, что при определении частных зависимостей во всех случаях эксперименты имели одну общую точку с координатами (t0; S0; V0). Тогда в этой точке величину PZ можно рассчитать как по общей, так и по частным зависимостям: PZ = CpZ × t Xp× S Yp× V Zp = CХ × t Xp = CY × S Yp = CZ × V Zp. ПОРЯДОК ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЕ РАБОТЫ
Последовательность выполнения работы: 1) изучить основные теоретические сведения по влиянию элементов режима резания на составляющие силы резания при продольном точении, методам измерения силы резания и конструкциям динамометров; 2) ознакомиться с методикой эксперимента и лабораторным оборудованием; 3) провести измерение главной составляющей силы резания РZ в зависимости от скорости, подачи и глубины резания; 4) по полученным данным построить графики функциональных зависимостей РZ = f (V), РZ = f (S), РZ = f (t); 5) обработать результаты измерений для получения эмпирической формулы вида PZ = CpZ×tXp×SYp×VZp; 6) по полученной эмпирической формуле рассчитать величину силы PZ для всех точек каждой серии опытов; 7) составить отчет по лабораторной работе. Отчет по лабораторной работе включает: 1) название и цель лабораторной работы; 2) схема измерения силы резания и эскиз конструкции динамометра; 3) заполненная таблица проведенного эксперимента (см. табл. 1); 4) графики для трех серий опытов; 5) графики в двойных логарифмических осях координат для трех серий опытов; 6) необходимые расчеты и полученные эмпирические зависимости; 7) выводы по лабораторной работе.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Силы, действующие на резец при продольном точении заготовки. 2. На какие составляющие разлагают равнодействующую силы резания? 3. Дать определение главной составляющей силы резания. 4. На чем основаны методы определения силы резания? 5. Назовите основные части динамометра. 6. Требования, предъявляемые к динамометрам. 7. Устройство механического динамометра. 8. Что такое тарировка динамометра? 9. Влияние толщины и ширины среза (глубины резания и подачи) на величину силы резания. 10. Характер и причины влияния скорости резания на величину силы резания.
ЛИТЕРАТУРА
1. Бобров В.Ф. Основы теории резания металлов. – М.: Машиностроение, 1975. – 344 с. 2. Егоров С.В., Червяков А.Г. Резание конструкционных материалов и режущий инструмент: Лабораторный практикум. – М.: Высшая школа, 1975. – 188 с. 3. Основы резания металлов и режущий инструмент / П.И. Ящерицын, М.Л. Еременко, Н.И. Жигалко. – Минск: Вышейшая школа, 1981. – 560 с. 4. Коженкова Т.И., Фельдштейн Е.Э. Лабораторные работы по резанию металлов. – Минск: Вышейшая школа, 1985. – 176 с. 5. Основы научных исследований / Под ред. В.И. Крутова. – М.: Высшая школа, 1989. – 400 с.
ИССЛЕДОВАНИЕ СИЛЫ РЕЗАНИЯ ПРИ ТОЧЕНИИ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 2357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.20.156 (0.016 с.) |

 .
.
 Рис. 2. Влияние скорости резания
на силу PZ, коэффициент усадки
стружки К и высоту нароста Н
Рис. 2. Влияние скорости резания
на силу PZ, коэффициент усадки
стружки К и высоту нароста Н
 Рис. 3. Тарировочный график
Рис. 3. Тарировочный график
 ,
,
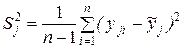 ,
, – среднее значение j-го опыта.
– среднее значение j-го опыта. ,
, к средней дисперсии опыта S 2:
к средней дисперсии опыта S 2: .
. ,
, – вычисленное по уравнению регрессии значение отклика в j-й точке;
– вычисленное по уравнению регрессии значение отклика в j-й точке; .
. (5)
(5)
 .
. .
.  ,
,
 .
.


