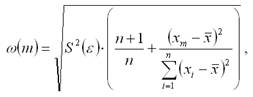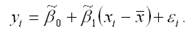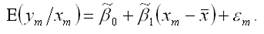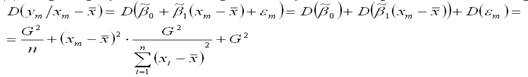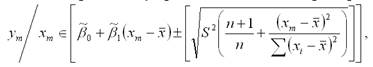Точечный и интервальный прогноз для модели парной регрессии

Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных моделей, с помощью которых можно спрогнозировать поведение результативной переменной в зависимости от поведения факторных переменных.

Рассмотрим подробнее процесс прогнозирования для линейной модели парной регрессии.

Точечный прогноз результативной переменной у на основе линейной модели парной регрессии при заданном значении факторной переменной хm будет осуществляться по формуле:

ym=β0+β1xm+εm.

Точечный прогноз результативной переменной ym с доверительной вероятностью γ или (1–а) попадает в интервал прогноза, определяемый как:

ym–t*ω(m)≤ ym≤ ym+t*ω(m),

t – t-критерий Стьюдента, который определяется в зависимости от заданного уровня значимости a и числа степеней свободы (n-2) для линейной модели парной регрессии;

ω(m) – величина ошибки прогноза в точке m.

Для линейной модели парной регрессии величина ошибки прогноза определяется по формуле:

где S2(ε) – несмещённая оценка дисперсии случайной ошибки линейной модели парной регрессии.

Рассмотрим процесс определения величины ошибки прогноза β(m).

Предположим, что на основе выборочных данных была построена линейная модель парной регрессии вида:

Факторная переменная х в данной модели представлена в центрированном виде.

Задача состоит в расчёте прогноза результативной переменной у при заданном значении факторной переменной хm, т. е.

Математическое ожидание результативной переменной у в точке m рассчитывается по формуле:

Дисперсия результативной переменной у в точке m рассчитывается по формуле:

где D(β0) – дисперсия оценки параметра β0 линейной модели парной регрессии, которая рассчитывается по формуле:

Следовательно, точечная оценка прогноза результативной переменной у в точке m имеет нормальный закон распределения с математическим ожиданием

и дисперсией

Если в формулу дисперсии результативной переменной у в точке m вместо дисперсии G2 подставить её выборочную оценку S2, то получим доверительный интервал для прогноза результативной переменной у при заданном значении факторной переменной хm:

где выборочная оценка генеральной дисперсии S2 для линейной модели парной регрессии рассчитывается по формуле:

 

 

В этом случае прогнозный интервал можно преобразовать к виду:

 

Компоненты временного ряда

Временным рядом называется ряд наблюдаемых значений изучаемого показателя, расположенных в хронологическом порядке или в порядке возрастания времени.

Отдельно взятый временной ряд можно представить как выборочную совокупность из бесконечного ряда значений показателей во времени.

Уровнями временного ряда называются наблюдения

из которых состоит данный ряд.

Временной ряд называется моментным рядом, если уровень временного ряда фиксирует значение изучаемого показателя на определённый момент времени.

Временной ряд называется интервальным рядом, если уровень временного ряда характеризует значение показателя за определённый период времени.

Временной ряд называется производным рядом, если уровни ряда представлены в виде производных величин (средних или относительных показателей).

Исследование данных, представленных в виде временных рядов, преследует две основные цели:

1) характеристика структуры временного ряда;

2) прогнозирование будущих уровней временного ряда на основании прошлых и настоящих уровней.

Достижение поставленных целей возможно с помощью идентификации модели временного ряда.

Идентификацией модели временного ряда называется процесс выявления основных компонент, которые содержит изучаемый временной ряд.

Временные ряды могут содержать два вида компонент – систематическую и случайную составляющие.

Систематическая составляющая временного ряда является результатом воздействия постоянно действующих факторов.

Выделяют три основных систематических компоненты временного ряда:

1) тренд;

2) сезонность;

3) цикличность.

Трендом называется систематическая линейная или нелинейная компонента, изменяющаяся во времени.

Сезонностью называются периодические колебания уровней временного ряда внутри года.

Цикличностью называются периодические колебания, выходящие за рамки одного года. Промежуток времени между двумя соседними вершинами или впадинами в масштабах года определяют как длину цикла.

Систематические составляющие характеризуются тем, что они могут одновременно присутствовать во временном ряду.

Случайной составляющей называется случайный шум или ошибка, которая воздействует на временной ряд нерегулярно.

К основным причинам, по которым возникает случайный шум, относят факторы резкого и внезапного действия, а также действия текущих факторов.

Катастрофическими колебаниями называется случайный шум, в основе возникновения которого лежат факторы резкого и внезапного действия.

Шум, в основе возникновения которого лежит действие текущих факторов, может быть связан также с ошибками наблюдений.

Отдельный уровень временного ряда обозначается как yt. Его можно представить в виде функции от основных компонент временного ряда следующим образом:

yt=f(T,S,C,ε),

где T – это трендовая компонента,

S – это сезонная компонента,

C – это циклическая компонента,

ε – случайный шум.

Существует несколько основных моделей временных рядов, к которым относятся:

1) аддитивная модель временного ряда, в которой компоненты представляют собой слагаемые:

yt=Tt+St+Ct+εt;

2) мультипликативная модель временного ряда, в которой компоненты представляют собой сомножители:

yt=Tt*St*Ct*εt;

3) комбинированная модель временного ряда:

yt=Tt*St*Ct+εt.