
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы фильтрации временного рядаСодержание книги Поиск на нашем сайте
етоды фильтрации временных рядов предназначены на решение проблем, возникающих при исследовании взаимосвязи между двумя и более временными рядами, с помощью исключения из них трендовой и сезонной компонент. К проблемам, которые позволяют устранить методы фильтрации временных рядов, относятся: 1) проблема ошибочности показателей тесноты и силы связи: а) если временные ряды, между которыми изучается взаимосвязь, содержат циклическую или сезонную компоненту одинаковой периодичности, то в результате значение показателей тесноты связи будет завышено; б) если один из временных рядов содержит циклическую или трендовую компоненту или периодичность совместных колебаний различна, то в результате значение показателей тесноты связи будет занижено; 2) проблема «ложной корреляции»: а) если временные ряды, между которыми изучается взаимосвязь, содержат тренды одинаковой направленности, то уровни этих рядов будут положительно коррелированны; б) если временные ряды, между которыми изучается взаимосвязь, содержат тренды противоположной направленности, то уровни этих рядов будут отрицательно коррелированны. Первая проблема решается путём исключения из временного ряда сезонной компоненты. Если временной ряд представлен в виде аддитивной модели, то сезонная компонента устраняется путём вычитания из исходных уровней ряда показателей абсолютных отклонений Sai. Если временной ряд представлен в виде мультипликативной модели, то сезонная компонента устраняется путём деления исходных уровней ряда на индексы сезонности Isi. Проблема “ложной корреляции” решается путём исключения из временного ряда трендовой компоненты. Предположим, что исследуется зависимость между двумя временными рядами – Х и Y. При этом была построена модель регрессии вида: Yt=β0+β1*Хt+εt. Для выявления «ложной корреляции» необходимо провести анализ остатков данной модели регрессии, потому что если в модели присутствует обычная автокорреляция остатков, следовательно, существует и «ложная автокорреляция». Исключение трендовой компоненты осуществляется с помощью метода отклонений от тренда. Алгоритм реализации метода отклонений от тренда: 1) вычисляются отклонения уровней временных рядов Yt и Xt от их значений, рассчитанных на основе уравнений тренда:
2) определяется степень тесноты связи между полученными отклонениями с помощью коэффициента корреляции:
3) для линейной модели регрессии строится модель зависимости отклонения e(yt) от e(xt): e(yt)=a0+a1* e(xt). Неизвестные коэффициенты данной модели рассчитываются с помощью классического метода наименьших квадратов по формулам:
В результате получим модель вида: e(yt)=a1* e(xt). Исключение трендовой компоненты можно также осуществить с помощью метода последовательных разностей. При этом рассчитываются разности между текущим и предыдущим уровнями для каждого временного ряда:
Далее рассчитывается показатель линейной корреляции абсолютных цепных приростов по формуле:
На основании показателей абсолютных цепных приростов можно построить линейную модель регрессии вида:
где а1 – это коэффициент, который уравнении характеризует в среднем прирост Y при изменении прироста Х на единицу своего измерения; а0 – это коэффициент, который характеризует прирост Y при нулевом приросте Х. С помощью разностных операторов первого порядка можно исключить автокорреляцию только в тех временных рядах, в которых основная тенденция выражена прямой линией. С помощью разностных операторов второго порядка можно исключить автокорреляцию в тех временных рядах, в которых основная тенденция выражена параболой второго порядка.
Гомоскедастичность и гетероскедастичность остатков модели регресиии. Гетероскедастичность Случайной ошибкой называется отклонение в линейной модели множественной регрессии: εi=yi–β0–β1x1i–…–βmxmi В связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается выборочная оценка случайной ошибки модели регрессии по формуле:
где ei – остатки модели регрессии. Термин гетероскедастичность в широком смысле понимается как предположение о дисперсии случайных ошибок модели регрессии. При построении нормальной линейной модели регрессии учитываются следующие условия, касающиеся случайной ошибки модели регрессии: 6) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
7) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:
8) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
Второе условие
означает гомоскедастичность (homoscedasticity – однородный разброс) дисперсий случайных ошибок модели регрессии. Под гомоскедастичностью понимается предположение о том, что дисперсия случайной ошибки βi является известной постоянной величиной для всех наблюдений. Но на практике предположение о гомоскедастичности случайной ошибки βi или остатков модели регрессии ei выполняется не всегда. Под гетероскедастичностью (heteroscedasticity – неоднородный разброс) понимается предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, что означает нарушение второго условия нормальной линейной модели множественной регрессии:
Гетероскедастичность можно записать через ковариационную матрицу случайных ошибок модели регрессии:
Тогда можно утверждать, что случайная ошибка модели регрессии βi подчиняется нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2Ω: εi~N(0; G2Ω), где Ω – матрица ковариаций случайной ошибки. Если дисперсии случайных ошибок
модели регрессии известны заранее, то проблема гетероскедастичности легко устраняется. Однако в большинстве случаев неизвестными являются не только дисперсии случайных ошибок, но и сама функция регрессионной зависимости y=f(x), которую предстоит построить и оценить. Для обнаружения гетероскедастичности остатков модели регрессии необходимо провести их анализ. При этом проверяются следующие гипотезы. Основная гипотеза H0 предполагает постоянство дисперсий случайных ошибок модели регрессии, т. е. присутствие в модели условия гомоскедастичности:
Альтернативная гипотеза H1 предполагает непостоянство дисперсиий случайных ошибок в различных наблюдениях, т. е. присутствие в модели условия гетероскедастичности:
Гетероскедастичность остатков модели регрессии может привести к негативным последствиям: 1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности; 2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.
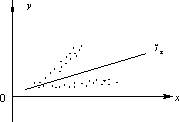
Гомоскедастичность Гомоскедастичность остатков означает, что дисперсия каждого отклонения одинакова для всех значений x. Если это условие не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции.
Т.к. дисперсия характеризует отклонение то из рисунков видно, что в первом случае дисперсия остатков растет по мере увеличения x, а во втором – дисперсия остатков достигает максимальной величины при средних значениях величины x и уменьшается при минимальных и максимальных значениях x. Наличие гетероскедастичности будет сказываться на уменьшении эффективности оценок параметров уравнения регрессии. Наличие гомоскедастичности или гетероскедастичности можно определять также по графику зависимости остатков от теоретических значений
|
|||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 628; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.62.85 (0.01 с.) |

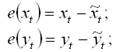


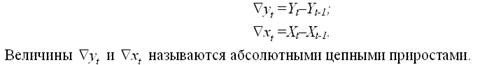


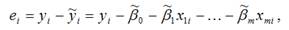
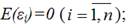





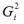
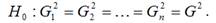


 .
.



