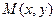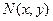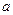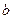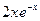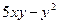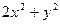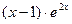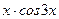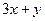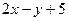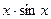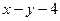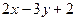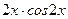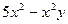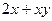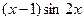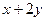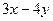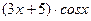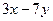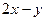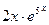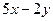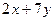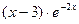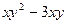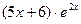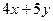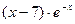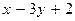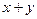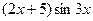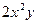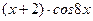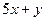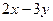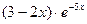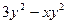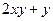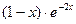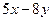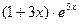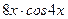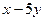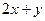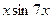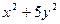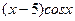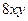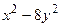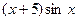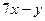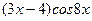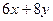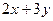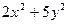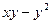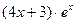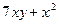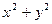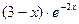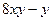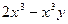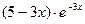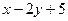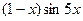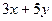Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема «Дифференциальные уравнения»Содержание книги
Поиск на нашем сайте
Выполнить следующие задания, выбрав соответствующие варианту величины из представленной ниже таблицы.
1. Найти общее решение дифференциального уравнения
2. Составить линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами а) б) в) г) Записать общее решение для каждого из составленных уравнений.
3. Найти общее решение линейного однородного дифференциального уравнения а) б) в) г)
4. Найти частное решение линейного однородного дифференциального уравнения
5. Найти общее решение линейного неоднородного дифференциального уравнения а) б) в) г) д)
6. Найти частное решение линейного неоднородного дифференциального уравнения
7. Найти общее решение дифференциального уравнения
Практическое занятие № 54 Тема занятия « Дифференциальные уравнения и методы их решения (итоговое занятие) »
Цель занятия: контроль теоретических знаний и практических умений по разделу «Дифференциальные уравнения». Организационная форма занятия: итоговое компьютерное тестирование. Компетенции, формируемые на занятии: - способность и готовность анализировать социально-значимые проблемы и процессы, использовать на практике методы гуманитарных, естественнонаучных, медико-биологических, и клинических наук в различных видах профессиональной и социальной деятельности (ОК-1); - способностью и готовностью к анализу медицинской информации при помощи системного подхода, к восприятию инноваций в целях совершенствования своей профессиональной деятельности, к использованию полученных теоретических, методических знаний и умений по фундаментальным естественнонаучным, медико-биологическим, клиническим и специальным (в том числе биохимическим) дисциплинам, в научно-исследовательской, лечебно-диагностической, педагогической и других видах работ (ПК-2, частично: формируется способность использовать методы математического анализа в научно-исследовательской деятельности). Формирование у будущих специалистов этих компетенций на занятии предполагает обучение студентов - сформулировать основные цели выполняемой работы; - анализировать ситуации и делать выводы; - ставить новые вопросы и видеть проблемы в традиционных ситуациях; - владеть основными методиками решения учебно-исследовательских задач; - вести поиск альтернативных средств и способов решения; - абстрагировать содержание и выделять существенное; - планировать самостоятельную работу; - осуществлять самоконтроль за работой, объективно оценивать ее результат. Вопросы, выносимые на обсуждение 1. Дифференциальные уравнения первого порядка. 2. Случаи понижения порядка дифференциального уравнения. 3. Линейные однородные и неоднородные дифференциальные уравнения второго и более высоких порядков. 4. Системы дифференциальных уравнений. 5. Приближенное решение дифференциальных уравнений. 6. Дифференциальные уравнения в частных производных. Методические рекомендации Для подготовки к занятию дома 1. Подготовьтесь к итоговому компьютерному тестированию по разделу «Дифференциальные уравнения».
2. Рекомендуется предварительно пройти репетиционное компьютерное тестирование. 3. Ответьте на вопросы тестов, приведенных в практических заданиях для развития и контроля владения компетенциями. На занятии по указанию преподавателя 1. Пройдите итоговое компьютерное тестирование по разделу «Дифференциальные уравнения». 2. Решите предложенный вариант самостоятельной работы №18 по теме «Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами». Дома 1. Подготовьтесь к коллоквиуму№4 по разделам «Функции нескольких переменных. Дифференциальные уравнения». Вопросы к коллоквиуму приведены в теоретических заданиях для развития и контроля владения компетенциями. 2. Подготовьтесь к контрольной работе № 5 по теме «Дифференциальные уравнения». Рекомендуемая литература [1] глава 13. [2] часть 2, глава IV. [3] глава 10. [4] часть III занятия 17 -21. [5] глава 6. [6] глава 15. [7] глава XV. Теоретические задания
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.77.29 (0.01 с.) |

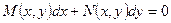 .
.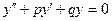 , если корни характеристического уравнения:
, если корни характеристического уравнения: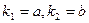 ;
;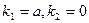 ;
;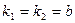 ;
;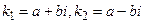
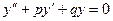 ;
;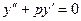 ;
;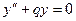 ;
;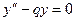 .
.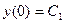 ,
, 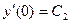 .
.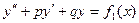 , где
, где 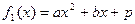 ;
;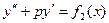 , где
, где 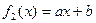 ;
;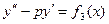 , где
, где 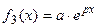 ;
;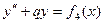 , где
, где 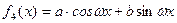 ;
;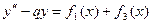 .
.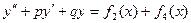 , отвечающее начальным условиям
, отвечающее начальным условиям 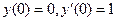 .
.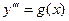 .
.