
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Программирование алгоритмов линейной структуры.Содержание книги
Поиск на нашем сайте
Текст программы на языке программирования C/С++ начинается с подключения заголовочных файлов, (#include <имя_модуля.h>), включающих описание средств вввода-вывода, используемых в программе. Для написания программы линейной структуры необходимо вспомнить: 1) запись констант, переменных, функций; 2) правила записи алгебраических выражений; 3) использование оператора присваивания; 4) организацию ввода-вывода данных. 5) стандартные фунции, которые могут использоваться в программе;
Задача 1. Найти сумму заданного трёхзначного числа а = 879 с числом, полученным из числа а перестановкой его цифр в обратном порядке. #include <iostream.h> //Подключение средств ввода-вывода С++ #include <conio.h> #include <stdio.h> //Подключение стандартных функций ввода-вывода С #include <math.h> //Подключение стандартных математических функций int main() {
int a=879; int z1, z2, z3, b=a; z3=a%10; //Вычисление младшей цифры числа a/=10; //Деление числа на 10 с отбрасыванием дробной части z2=a%10; //Вычисление второй цифры числа z1=a/10; // Вычисление третьей цифры числа cout<<((100*z3+10*z2+z1)+b);//Вычисление и вывод результата на экран getch(); //Задержка экрана пользователя для просмотра результата (из conio.h) return 0; }
Задача 2. Следующая программа запрашивает длину в дюймах, затем преобразует ее в сантиметры (1 дюйм = 2.54 см) и выдает полученное значение на экран.
#include <iostream.h> #include <conio.h> int main () { int duim; cout<<"введи длину в дюймах"; cin>>duim; cout <<duim<<" дюймов= "<<duim*2.54<<" см\n"; getch();return 0; }
Задача 3. Присвоить целой переменной Z первую цифру из дробной части числа А (например, если А = 123.948, то Z = 9) //из_дроб.cpp #include <conio.h> #include <stdio.h> #include <math.h> int main() { double A =123.948; int Z; clrscr(); printf("A= %lf\n",A); A = A - int (A); Z = int (A*10); printf("A= %lf\n",A); printf("Z= %d\n",Z); getch();return 0; }
Задача 4. Поменять местами значения целых переменных a и b: a) используя вспомогательную переменную; б) без применения вспомогательной переменной. //обмен.cpp #include <conio.h> #include <stdio.h> #include <math.h> int main() { int a=15, b=-7, t; clrscr(); //Очистка экрана
// 1 вариант t=a; a=b; b=t; printf("a= %d\n",a); printf("b= %d\n",b);
// 2 вариант a=a+b; b=a-b; a=a-b; printf("a= %d\n",a); printf("b= %d\n",b);
// 3 вариант a=a^b; b=a^b; a=a^b; printf("a= %d\n",a);
printf("b= %d\n",b);
getch();return 0; }
Введем длину основания a и угол
Далее, из рисунка видно, что высота треугольника h может быть найдена по формуле:
а боковая сторона
Остальное, как говорят, дело техники. Ниже приведена соответствующая программа.
//площа_3.cpp #include <conio.h> #include <stdio.h> #include <math.h> const double pi= 3.14159; int main() { float a, c, psy, h,s; int alpha; clrscr(); printf("Введи основание "); scanf("%f",&a); printf("Введи угол в градусах "); scanf("%d",&alpha); //преобразуем угол в радианы psy=pi*alpha/180; //найдем высоту h =a*tan(psy)/2; //вычислим площадь s=0.5*a*h; printf("Площадь= %10.2f\n",s); //найдем боковую сторону c = h/sin(psy); printf("Периметр= %10.2f\n",a + 2*c); getch();return 0;
}
Протокол выполнения программы:
Введи основание 6 Введи угол в градусах 60 Площадь= 15.59 Периметр= 18.00
Задача 6. Ввести координаты трёх точек на плоскости: (х1, у1), (х2, у2), (х3, у3). Определить, лежат ли они на одной прямой. Если три точки лежат на одной прямой, то площадь треугольника, образованная соединяющими их отрезками, очевидно, равна нулю. Площадь S треугольника, заданного координатами его вершин (х1, у1), (х2, у2), (х3, у3), определяется формулой:
S =
Раскрыв определитель третьего порядка по последнему столбцу, получим:
S =
Замечание. Значение S положительно, если направление обхода вершин треугольника совпадает с положительным направлением вращения (т.е. против часовой стрелки).
//три_точк.cpp Три точки на одной прямой? #include <conio.h> #include <stdio.h> #include <math.h> int main() { double x1,y1,x2,y2,x3,y3,s; printf("Введи через пробел координаты вершин:\n"); printf("x1 y1 "); scanf("%lf %lf",&x1, &y1); printf("x2 y2 "); scanf("%lf %lf",&x2, &y2); printf("x3 y3 "); scanf("%lf %lf",&x3, &y3); s=0.5*(x2*y3 - x3*y2 - x1*y3 +x3*y1 + x1*y2 - x2*y1); printf("s = %lf\n", s); printf("Три точки на одной прямой "); printf("%s \n",(fabs(s)<=0.000001)?("лежат"):(" не лежат")); getch();return 0; }
Протокол работы программы:
Введи через пробел координаты вершин:
x1 y1 0 0 x2 y2 2 0 x3 y3 0 2 s = 2.000000 Три точки на одной прямой не лежат
Для вывода результата тестирования мы здесь воспользовались тернарной операцией. Следует помнить, что сравнивать между собой вещественные числа на равенство – неблагодарное дело (ведь они в памяти представлены приближённо!).
Задача 7. Программа иллюстрирует некоторые особенности последовательного применения операций "инкремент" и "декремент" в выражениях. В частности, не следует забывать, что эти операции в выражении вычисляются в порядке их следования справа налево; этим и объясняются несколько неожиданные на первый взгляд результаты работы программы. #include <stdio.h> #include <iostream.h> #include <conio.h> int main () { int y,n; clrscr(); n = 5; y = n/2+5*(1 + n++)+n/2; cout<<"n = "<<n<<" y = "<<y<<endl; //n=6 y=34 n = 5; y = n++ + ++n; cout<<"n = "<<n<<" y = "<<y<<endl; //n=7 y=12 n = 5; y = n++ + --n; cout<<"n = "<<n<<" y = "<<y<<endl; //n=5 y=8 n = 0; y = (n = 5) + (++n); cout<<"n = "<<n<<" y = "<<y<<endl; //??? n=5 y=10 getch();return 0;
}
Результаты работы программы:
n=6 y=34 n=7 y=12 n=5 y=8 n=5 y=10???
Последний результат трудно объяснить. Для того же примера компиляторы GNU gcc и g++ в операционной системе Linux дают более ожидаемый результат:
n=6 y=11
Задача 8. Следующая программа иллюстрирует работу поразрядных логических операций и сдвигов. Прежде чем вы возьметесь за осмысление полученных результатов, непременно разберитесь со внутренним (машинным) представлением целочисленных величин. Напомним, что эти данные хранятся в двоичном коде (положительные – в прямом, а отрицательные – в дополнительном коде). Шестнадцатеричная система счисления служит для компактной записи двоичных данных. При этом каждая шестнадцатеричная цифра кодируется 4 двоичными разрядами: 0 – 0000, 1 – 0001, 2 – 0010, 3 – 0011, 4 – 0100, 5 – 0101, 6 – 0110, 7 – 0111, 8 – 1000, 9 – 1001, A – 1010, B – 1011, C – 1100, D – 1101, E – 1110, F – 1111.. Цифры восьмеричной системы счисления кодируются 3 двоичными разрядами: 0 – 000, 1 – 001, 2 – 010, 3 – 011, 4 – 100, 5 – 101, 6 – 110, 7 – 111.
#include "stdafx.h" #include <conio.h> #include <stdio.h>
int main() { unsigned char c; unsigned short int n, m=125; printf("%d %X %o\n",m,m,m); // 125 7D 175 n=m & 017; printf("%d %X %o\n",n,n,n); // 13 D 15 n=m | 013; printf("%d %X %o\n",n,n,n); // 127 7D 177 n=m>>3; printf("%d %X %o\n",n,n,n); // 15 F 17 n=m<<2; printf("%d %x %o\n",n,n,n); // 500 1F4 764 c=~m; printf("%d %X %o\n",c,c,c); // 130 82 202 n=m^013; printf("%d %X %o\n",n,n,n); // 118 76 166 _getch(); return 0; }
Результат работы программы приведен в виде комментария к каждому из операторов вывода.
Задача 9. С интервалом в 0.7 секунды играть все ноты малой октавы: до, до-диез, ре, ре‑диез, ми, …, си.
// Программа отлажена в Visual Studio 2008 #include <Windows.h> #include <iostream> using namespace std;
int main() { const int d=700; Beep(130.8, d); Beep(138.6, d); Beep(146.8, d); Beep(155.6, d); Beep(164.8, d); Beep(174.6, d); Beep(185.0, d); Beep(190.0, d); Beep(207.7, d); Beep(220.0, d); Beep(233.1, d); Beep(246.9, d); return 0; }
Замечание. В этом примере использована новая для нас функция Beep(). Здесь и далее, чтобы выяснить назначение и правила применения неизвестных вам функций стандартной библиотеки языка, поступите следующим образом: подгоните курсор под имя неизвестной функции и нажмите клавишу F1. В частности, таким способом Вы узнаете, что функция Beep() генерирует звуковой сигнал заданной частоты в герцах (первый аргумент); длительность звучания каждой ноты в миллисекундах задает второй аргумент. И не забудьте вставить препроцессорную команду #include<Windows.h> (или #include <vcl.h> для Borland С++ Builder).
При необходимости приостановку выполнения программы на заданное число миллисекунд можно осуществить при помощи функции Sleep(). Исследуйте её самостоятельно.
1. Обьем круглого конуса равен V = p r 2 h, где: r — радиус основания, h — высота. Составить программу для вычисления объема. 2. Площадь равностороннего треугольника с заданной стороной а вычисляется по формуле: S = a2. Составить программу для вычисления площади. 3. Вычислить высоты треугольника со сторонами a, b, c по формулам: ha =, hb =, hc =, где p = (a + b + c). 4. Смешано V Tcм =, Vcм = V1 + V2.
5. Присвоить целой переменной Z третью от конца цифру в записи целого положительного числа А (например, если А = 475984, то Z = 9).
6. Две точки на плоскости заданы своими координатами (x1, y1) и (x2, y2). Найти расстояние между ними.
S = h(R + r)l + pR2 + pr2 и его обьем V = p h(R 2 + r 2 + Rr) Здесь R, r — радиусы оснований h — высота l — образующая
9. Радиус окружности, вписанной в равносторонний треугольник, равен R. Составить программу для вычисления площади двумя способами: а) по длине основания и высоте; б) по формуле Герона
10. Обьем круглого цилиндра равен V = p r 2h, где: r — радиус основания, h — высота
11. Площадь правильного шестиугольника со стороной а вычисляется по формуле: S = a2. Cоставить программу для вычисления площади.
12. Ввести три стороны треугольника a, b, c. Вычислить его площадь по формуле Герона:
S =
где p = (a + b + c). Найти одну из высот треугольника.
13. Вычислить медианы треугольника по трем его сторонам a, b, c:
mb = mc =
14. Площадь кругового кольца, у которого R и r — внешний и внутренний радиусы, R¢ — средний радиус, K — ширина кольца, вычисляется по формулам: S1 = p(R2 – r2), S1 = 2 pR¢K
15. Пусть D — диаметр основания цилиндра, H — его высота. Составить программу для вычисления его поверхности S и объема V:
16. Ввести сторону квадрата а. Вычислить и выдать на экран длину окружности:
а) вписанной в него; б) описанной около него.
17. Ввести сторону квадрата а. Найти площадь незаштрихованной части фигуры. Указание. Радиусы дуг образовавшихся секторов равны половине стороны квадрата.
18. Ввести сторону равностороннего треугольника а. Найти площадь фигуры, ограниченной дугами. Указание. Радиусы дуг образовавшихся секторов равны половине стороны треугольника.
Составить программу для вычисления площади заштрихованной части фигуры.
21. Треугольник задан величинами своих углов и радиусом описанной окружности. Найти стороны треугольника.
22. Найти площадь равнобочной трапеции с основаниями а и в и углом α при большем основании.
23. Даны действительные положительные числа а, в, с. По трём сторонам с длинами а, в, с можно построить треугольник. Найти углы треугольника.
24. Дана длина куба. Найти площадь полной поверхности и объём этого куба.
25. Дано х. Вычислить 2х4– 3х3 + 4х2 – 5х + 6, применив не более 8 операций сложения, вычитания и умножения.
26. Определить силу притяжения F между двумя телами массы m1 и m2, находящимися на расстоянии r друг от друга.
27. Даны гипотенуза и катет прямоугольного треугольника. Найти второй катет и радиус вписанной окружности.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 2376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.216.107 (0.012 с.) |

 Задача 5. В равнобедренном треугольнике основание равно а, а угол при основании равен
Задача 5. В равнобедренном треугольнике основание равно а, а угол при основании равен  . Найти площадь и периметр треугольника.
. Найти площадь и периметр треугольника. . Прежде всего, преобразуем угол из градусной меры в радианную:
. Прежде всего, преобразуем угол из градусной меры в радианную:

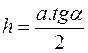


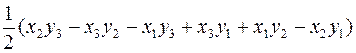
 Задачи для самостоятельного решения
Задачи для самостоятельного решения литров воды температуры T1 и V2 литров воды температуры T2 . Написать программу вычисления объема и температуры образовавшейся смеси по формулам:
литров воды температуры T1 и V2 литров воды температуры T2 . Написать программу вычисления объема и температуры образовавшейся смеси по формулам: 7. Найти площадь равнобочной трапеции с основаниями А и В и углом b при большем основании.
7. Найти площадь равнобочной трапеции с основаниями А и В и углом b при большем основании. 8. Вычислить площадь поверхности усеченного конуса
8. Вычислить площадь поверхности усеченного конуса Результаты сравнить.
Результаты сравнить. Составить программу для вычисления объема
Составить программу для вычисления объема

 ma =
ma = Ввести R и r. Найти R¢ и K. Вычислить площадь по обеим формулам и сравнить результаты.
Ввести R и r. Найти R¢ и K. Вычислить площадь по обеим формулам и сравнить результаты. S = + pDH, V = pD2H
S = + pDH, V = pD2H

 19. Около квадрата со стороной а описана окружность, в него вписана другая окружность. Составить программу, которая вводит значение а и вычисляет площадь образовавшегося кольца.
19. Около квадрата со стороной а описана окружность, в него вписана другая окружность. Составить программу, которая вводит значение а и вычисляет площадь образовавшегося кольца. 20. Две окружности имеют внутреннее касание. Радиус большей из них равен R1, а радиус меньшей – в два раза меньше (см. рис).
20. Две окружности имеют внутреннее касание. Радиус большей из них равен R1, а радиус меньшей – в два раза меньше (см. рис).


