
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды сбалансированных деревьев, достоинства и недостатки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ДЕРЕВО ОПТИМАЛЬНОГО ПОИСКА
Бывают случаи, когда информация о вероятности появления ключа известна. В таких ситуациях характерно постоянство ключей, то есть ключи не добавляются, не удаляются, и сохраняется структура дерева. И для сокращения времени необходимо использование таких деревьев, в которых самые часто встречающиеся вершины находились бы ближе к корню дерева.
1) Будем рассматривать дерево с псевдовершинами. Т. е. обнаружение того факта, что некий ключ k не является ключом в дереве поиска, можно рассматривать,как обращение к псевдовершине (псевдоузлу), вставленной между ближайшими меньшим и большим ключами.
2) Вместо вероятности
(Если поделить 3) Длина средневзвешенного пути:
n – количество вершин, m – количество псевдовершин, ai, bi – вершина и псевдовершина соответственно, hi, hj – уровень вершины, псевдовершины соответственно. Свойство: Любое поддерево дерева оптимального поиска является оптимальным. Т. е. если дерево оптимального поиска разделим пополам относительно вершины, то левои и правое поддерево по основному свойству будут также оптимыльными.
Тогда длина средневзвешенного пути для левого поддерева:
Длина средневзвешенного пути для правого поддерева
W – вес дерева оптимального поиска – количество всех возможных поисков.
Построение дерева: 1) Построение таблицы весов, 2) Достраиваем таблицу, 3) Таблица путей, 4) Сложность
КРАСНО-ЧЕРНЫЕ ДЕРЕВЬЯ.
Свойства: 1) Каждая вершина имеет цвет – красный или черный, 2) Если вершина красная, то оба ее потомка черные, 3) Все пути, ведущие от корня к листьям, содержат одинаковое количество черных вершин.
Красно-черное является подмножеством СДБ, в котором каждый узел может содержать от 1 до 3 значений и, соответственно, от 2 до 4 указателей на потомков. Можно «поднять» красные узлы в графическом представлении красно-черного дерева так, чтобы они оказались на одном уровне по горизонтали со своими предками черными узлами, образуя страницу, тогда будет видно, что горизонтальная ссылка всегда указывает на красную вершину, а вертикальная – на черную.
SPLAY-ДЕРЕВЬЯ. Расширяющееся дерево является двоичным деревом поиска, в котором поддерживается свойство сбалансированности. Это дерево принадлежит классу «саморегулирующихся деревьев», которые поддерживают необходимый баланс ветвления дерева, чтобы обеспечить выполнение операций поиска, добавления и удаления за логарифмическое время от числа хранимых элементов. Это реализуется без использования каких-либо дополнительных полей в узлах дерева (как, например, в Красно-чёрных деревьях или АВЛ-деревьях, где в вершинах хранится, соответственно, цвет вершины и глубина поддерева). Вместо этого «расширяющие операции» (splay operation), частью которых являются вращения, выполняются при каждом обращении к дереву. Учётная стоимость в расчёте на одну операцию с деревом составляет O (logn). Идея: после обращения к вершине мы поднимаем ее к корню. Операции: Splay (расширение) Основная операция дерева. Заключается в перемещении вершины в корень при помощи последовательного выполнения трёх операций: Zig, Zig-Zig и Zig-Zag. Обозначим вершину, которую хотим переместить в корень за x, её родителя - p, а родителя p (если существует) - g. · Zig: выполняется, когда p является корнем.
· Zig-Zig: выполняется, когда и x, и p являются левыми (или правыми) сыновьями. Дерево поворачивается по ребру между g и p, а потом - по ребру между p и x.
· Zig-Zag: выполняется, когда x является правым сыном, а p - левым (или наоборот). Дерево поворачивается по ребру между p и x, а затем - по ребру между x и g.
С одной стороны, Поиск элемента: Если ключ найден, то применяется splay к нему. Иначе применяется к последней вершине, к которой осуществлялся доступ. Добавление элемента: Вставка ->Splay Пример:
Удаление ->Splay к родителю Пример:
Объединение двух деревьев:
t1 t2 Ищем максимальную вершину в t1, проводим с ней splayи ставим ее в корень нового дерева. Split (разделение дерева на две части): Поиск и splayвершины х, по которой будем делить ->Разделяем либо по одному, либо по второму ребру.
АСОЦИАТИВНЫЕ МАССИВЫ И ХЭШИ
Массивы, в которых для обращения к элементам используются ключи, логически связанные со значениями, называют ассоциативными массивами.
Хэш-функции Основным требованиям к хорошей хэш-функции является наиболее равномерное из возможных распределение ключей по диапазону значений индексов. Кроме выполнения этого требования, распределение не связано никакой схемой, и даже желательно, чтобы оно производило впечатление совершенно случайного. Предположим, что имеется функция ord(k), которая определяет порядковый номер ключа k во множестве всех возможных значений ключей. Предположим также, что индексы массива занимают интервал целых чисел 0... N— 1, где N — размер массива. Тогда очевидно, что нужно выбрать следующую функцию: Н (k) = ord(k) mod N.Для нее характерно равномерное распределение ключей на всем интервале индексов, поэтому она служит основой большинства преобразований ключей. Кроме того, она очень эффективно вычисляется при N, равном степени двойки. Но как раз этого случая следует избегать, если ключи являются последовательностями букв: предположение, что все ключи равновероятны, в этом случае совершенно ошибочно, в результате слова, различающиеся лишь несколькими символами, будут с большой вероятностью отображаться в одинаковые индексы, что приведет к чрезвычайно неравномерному распределению. Ситуация, когда в указанном месте нет элемента с заданным ключом, называется конфликтом. Задача формирования альтернативного индекса – решение конфликта.Если обнаруживается, что строка таблицы, соответствующая заданному ключу, не содержит желаемого элемента, то произошел конфликт, т. е. два элемента имеют такие ключи, которые отображаются в один и тот же индекс. В этом случае нужно сформировать еще один индекс. Существует несколько методов формирования вторичного индекса (разрешения конфликтов): 1) Прямое связывание – связывание в линейный список всех строк с идентичным первичным индексом H(k). Но тогда необходимо следить за вторичными списками и в каждой строке отводить место для ссылки (или индекса) на соответствующий список конфликтных элементов. 2) Открытая адресация – нужно просматривать другие строки этой же таблицы до тех пор, пока не найдется желаемый элемент или пустая строка (тогда считаем, что ключа в таблице нет).
В этом случае алгоритм просмотра будет выглядеть следующим образом: h=H(k); i=0;do{ if (T[h] == k) { элемент найден; } else if T[h] = свободно { элемента нет в таблице; } else // конфликт i=i+l, h=H(k) + G(i); // G(i)- функция разрешения конфликтов}while (! Найден || нет в таблице || таблица полна) Выбор G(i):1) Линейные пробы  Недостаток – строки имеют тенденцию группироваться вокруг первичных ключей, т. е. тех, для которых при включении конфликта не возникало.2) Квадратичные пробы Недостаток – строки имеют тенденцию группироваться вокруг первичных ключей, т. е. тех, для которых при включении конфликта не возникало.2) Квадратичные пробы  Недостаток – при поиске пробуются не все строки таблицы. Анализ метода: Недостаток – при поиске пробуются не все строки таблицы. Анализ метода: Будем полагать, что все допустимые ключи равновероятны, и функция расстановки равномерно отображает их на весь диапазон индексов таблицы. Пусть в таблице размера n уже содержится k элементов.
Среднее число попыток при включении (k+1) элемента
Теперь можно вычислить среднее число попыток, необходимых для доступа к таблице к некоторому случайному ключу. Пусть n – размер таблицы, m – число ключей, фактически помещенных в таблицу. Тогда:
где Если подставить
Среднее число попыток в зависимости от коэффициента заполнения:
Реальные методы разрешения конфликтов дают несколько худшую производительность.
Недостатки: фиксированный размер таблиц и невозможность настройки на реальные требования, изъятие сроки из расстановочной таблицы – трудоемкая операция. Поэтому, когда объемы данных неизвестны и сильно варьируются, то лучше будет организация памяти в виде деревьев.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1077; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.236.101 (0.011 с.) |

 )
)

 , будем рассматривать:
, будем рассматривать: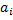 – число поисков вершины
– число поисков вершины  ;
; – число поисков псевдовершины
– число поисков псевдовершины  ,
,  .
. на N, то получится та же самая вероятность)
на N, то получится та же самая вероятность)



 – вес дерева
– вес дерева  (дерево с ключами
(дерево с ключами  ;
; ;
; ;
; .
. .
.



 –сложность доступа, n – количество вершин. В данном случае дерево ведет себя как сбалансированное. С другой стороны, если к каждому элементу осуществлялся хотя бы 1 доступ, то дерево ведет себя как дерево оптимального поиска, т. е. сложность доступа составляет
–сложность доступа, n – количество вершин. В данном случае дерево ведет себя как сбалансированное. С другой стороны, если к каждому элементу осуществлялся хотя бы 1 доступ, то дерево ведет себя как дерево оптимального поиска, т. е. сложность доступа составляет 
 Удаление элемента:
Удаление элемента:






 – гармоническая функция; g – эйлерова константа.
– гармоническая функция; g – эйлерова константа.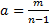 – коэффициент заполнения (приблизительно соответствует отношению занятой памяти по всей имеющейся), то
– коэффициент заполнения (приблизительно соответствует отношению занятой памяти по всей имеющейся), то



