
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Траектория сбалансированного ростаСодержание книги Поиск на нашем сайте Поскольку Итак, из модели Солоу следует, что независимо от начального состояния экономика стремится к траектории сбалансированного роста – к траектории, на которой каждая переменная модели растет с постоянным темпом. Темп роста выпуска на одного работника на траектории сбалансированного роста определяется только темпом технического прогресса.[12] Влияние изменения нормы сбережений Параметром модели Солоу, на который вероятнее всего воздействует экономическая политика, является норма сбережений. Деление государственных закупок на потребление и государственные инвестиции, выбор между долговым и налоговым финансированием расходов бюджета, налогообложение сбережений и инвестиций, - все это, вероятно, влияет на инвестируемую долю выпуска. Для определенности, рассмотрим экономику Солоу, находящуюся изначально на траектории сбалансированного роста, и предположим, что происходит перманентное увеличение Влияние на выпуск Увеличение Рисунок 1.4 Воздействие нормы сбережений на фактические инвестиции. Эти рассуждения отражены на первых трех графиках рисунка 1.5. Рисунок 1.5. Результаты увеличения нормы сбережений. Особый интерес для нас представляет динамика выпуска на одного работника, Четвертый и пятый график на рисунке 1.5. показывают, как сбережения влияют на динамику душевого выпуска. Темп роста выпуска на одного работника, изначально равный Таким образом, изменение нормы сбережений оказывает воздействие на уровень, но не воздействие на рост: это изменяет траекторию сбалансированного роста, а значит и выпуск на одного работника в любой момент времени, но не влияет на темпы роста выпуска на одного работника на траектории сбалансированного роста. На самом деле, в модели Солоу только изменение темпов технического прогресса оказывает воздействие на рост; любые другие изменения оказывают воздействие лишь на уровень. (Лит. Редактору: «воздействие» - термин, не заменять. «Влияние» - другое слово. В.П.) Влияние на потребление Если бы мы ввели в модель домашние хозяйства, тогда их благосостояние зависело бы не от выпуска, а от потребления: инвестиции это лишь фактор производства в будущем. Следовательно, для анализа многих вопросов мы более заинтересованы в анализе динамики потребления, чем динамики выпуска. Потребление на единицу эффективного труда равняется выпуску на единицу эффективного труда В общем случае не ясно, превысит ли потребление свой первоначальный уровень. Обозначим через
Величина
Мы знаем, что рост Производная Рисунок 1.6. Выпуск, инвестиции и потребление на траектории сбалансированного роста. На нижнем графике Количественные оценки Очень часто нас интересуют не только качественные выводы из рассматриваемой модели, но также и количественные оценки. Если, например, последствием небольшого воздействия на норму сбережений является значительное изменение темпов роста на протяжении нескольких столетий, то утверждение, что это воздействие является временным, не представляет особого интереса. Для большинства моделей, включая модель Солоу, для получения точных численных оценок требуется выбрать конкретные функциональные формы и значения параметров; зачастую также требуется провести численный анализ модели. Однако во многих случаях многое можно понять, рассматривая аппроксимацию модели в окрестности долгосрочного равновесия. Этим подходом мы сейчас и воспользуемся.
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1038; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.011 с.) |

 стремится к
стремится к  , естественно задаться вопросом, как себя ведут основные переменные модели, когда
, естественно задаться вопросом, как себя ведут основные переменные модели, когда 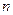 и
и  . Запас капитала
. Запас капитала 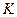 равняется
равняется  ; так как
; так как  (т.е.
(т.е.  равняется
равняется  растет с тем же темпом. Капитал на одного работника
растет с тем же темпом. Капитал на одного работника  и выпуск на одного работника
и выпуск на одного работника  растут с темпом
растут с темпом  . В результате этого эксперимента мы не только продемонстрируем выводы из модели, касающиеся влияния нормы сбережений, но и проиллюстрируем свойства модели в ситуации, когда экономика не находится на траектории сбалансированного роста.
. В результате этого эксперимента мы не только продемонстрируем выводы из модели, касающиеся влияния нормы сбережений, но и проиллюстрируем свойства модели в ситуации, когда экономика не находится на траектории сбалансированного роста.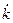 – положительно. Следовательно, капиталовооруженность эффективного труда
– положительно. Следовательно, капиталовооруженность эффективного труда 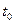 – это момент времени, когда происходит увеличение нормы сбережений. Мы предположили, что
– это момент времени, когда происходит увеличение нормы сбережений. Мы предположили, что  . Если
. Если 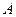 . Когда
. Когда 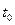 , а затем плавно возвращается на свой первоначальный уровень. Следовательно, выпуск на одного работника сначала увеличивается по сравнению с начальной траекторией, а затем стабилизируется на более высокой траектории, которая параллельна первоначальной[14].
, а затем плавно возвращается на свой первоначальный уровень. Следовательно, выпуск на одного работника сначала увеличивается по сравнению с начальной траекторией, а затем стабилизируется на более высокой траектории, которая параллельна первоначальной[14].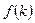 , умноженному на норму потребления
, умноженному на норму потребления  . Так как
. Так как  - потребление на единицу эффективного труда на траектории сбалансированного роста. Очевидно,
- потребление на единицу эффективного труда на траектории сбалансированного роста. Очевидно,  , за вычетом инвестиций на единицу эффективного труда,
, за вычетом инвестиций на единицу эффективного труда,  . На траектории сбалансированного роста фактические инвестиции равняются восстанавливающим,
. На траектории сбалансированного роста фактические инвестиции равняются восстанавливающим,  . Следовательно,
. Следовательно, (1.19)
(1.19)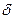 ; значит, мы можем записать
; значит, мы можем записать  . Тогда из выражения (1.19) получаем:
. Тогда из выражения (1.19) получаем: (1.20)
(1.20)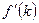 , чем
, чем  , увеличение нормы сбережений может приводить как к увеличению, так и к уменьшению потребления в долгосрочной перспективе. Если
, увеличение нормы сбережений может приводить как к увеличению, так и к уменьшению потребления в долгосрочной перспективе. Если  , умноженную на изменение
, умноженную на изменение  превышает
превышает 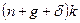 и
и 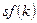 , но также и
, но также и  определяется расстоянием между
определяется расстоянием между 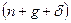 , поэтому увеличение нормы сбережений приводит к сокращению потребления даже когда экономика достигает новой траектории сбалансированного роста. На среднем графике наблюдается обратная картина, и увеличение
, поэтому увеличение нормы сбережений приводит к сокращению потребления даже когда экономика достигает новой траектории сбалансированного роста. На среднем графике наблюдается обратная картина, и увеличение  : линии
: линии 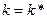 . В этом случае предельное изменение
. В этом случае предельное изменение 


