
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Воздействие на выпуск в долгосрочной перспективеСодержание книги
Поиск на нашем сайте
Долгосрочное воздействие увеличения нормы сбережений на выпуск определяется следующим выражением:
где
Выражение (1.22) выполняется для любых значений
где аргументы функции
Подстановка (1.24) в (1.21) дает:
Два преобразования помогают проинтерпретировать это выражение. Во-первых, помножим обе его части на
где
Если рынки конкурентны и нет внешних эффектов, то цена капитала равна его предельной производительности. В этом случае общая сумма, которая идет на оплату капитала (на единицу эффективного труда) на траектории сбалансированного роста, равна Доля капитала в совокупном доходе для большинства стран составляет примерно одну треть. Если мы используем это в качестве оценки На интуитивном уровне нетрудно понять, что при малых значениях Скорость сходимости На практике нас интересует не только долгосрочный эффект некоторых воздействий (таких, как изменение нормы сбережений), но и насколько быстро этот эффект реализуется. Опять-таки, можно использовать аппроксимацию модели в окрестности точки долгосрочного равновесия, чтобы ответить на этот вопрос. Для простоты сосредоточимся на поведении
То есть, Обозначим через
Так как Из уравнения (1.29) следует, что в окрестности траектории сбалансированного роста капиталовооруженность
где Осталось определить
где в третьей строчке мы использовали соотношение Мы можем подобрать параметры (1.31), чтобы оценить, насколько быстро экономика стремится к траектории сбалансированного роста. Обычно 1.6 Модель Солоу и основные вопросы теории роста Модель Солоу выявляет две возможные причины межвременных или межстрановых различий в уровнях душевого выпуска: различия в капиталовооруженности труда Существуют два способа показать, почему из модели Солоу следует данный вывод: один способ прямой, другой – косвенный. Прямой подход – это оценка необходимых различий в капиталовооруженности. Предположим, что мы пытаемся объяснить межстрановое различие в выпуске на одного работника в Выпуск на одного работника в индустриальных странах за последние 100 лет вырос примерно в 10 раз; отношение выпуска в индустриальных странах к выпуску в беднейших странах имеет примерно такой же порядок. Следовательно, мы хотим объяснить значение переменной Эмпирические данные не подтверждают столь значительных различий в запасе капитала. Отношение капитала к выпуску приблизительно постоянно во времени. Следовательно, капиталовооруженность труда в индустриальных странах за последние 100 лет выросла примерно в 10 раз, а не в 100 и не в 1000 раз. Аналогично, межстрановые различия в капиталовооруженности хоть и значительны, но не столь велики. Например, отношение капитала к выпуску в индустриальных странах приблизительно в 2-3 раза больше этого отношения в бедных странах; следовательно, капиталовооруженности различаются «лишь» в 20-30 раз. Итак, различия в капиталовооруженности недостаточны для того, чтобы объяснить различия в доходах на одного работника, которые мы пытаемся понять[19]. Косвенный способ убедиться в неспособности модели объяснить значительные различия в выпуске на одного работника заключается в демонстрации того, что требуемые для объяснения различия в капиталовооруженности влекут за собой неправдоподобно большие различия в предельной отдаче от капитала (см. Лукас (Lucas, 1990)). Если рынки являются конкурентными, то ставка процента равна предельной производительности капитала
Выражение (1.32) показывает, что эластичность предельной отдачи от капитала по выпуску равна Как и в случае с капиталовооруженностью, мы не наблюдаем таких различий в ставках процента. Прямые оценки отдачи от капитала на финансовых рынках показывают лишь незначительные вариации этого показателя во времени или между странами. Более показательными являются оценки межстрановых различий, построенные на основе анализа того, куда инвестируют владельцы капитала. Если бы ставка процента была в 10 или 100 раз выше в бедных странах, чем в богатых, то существовали бы огромные стимулы для того, чтобы инвестировать именно в бедные страны. При подобных различиях в предельной производительности капитала, влияние таких факторов, как несовершенство финансового рынка, налоговая политика, риск экспроприации, и т. д., отошло бы на второй план, и мы наблюдали бы мощный поток инвестиций из богатых стран в бедные. Мы не наблюдаем этих потоков[20]. Следовательно, если мы полагаем, что вклад капитала в выпуск примерно соответствует его рыночной цене, то мы не можем объяснить различий в выпуске на одного работника различиями в капиталовооруженности. Другой возможной причиной различий выпуска на одного работника в модели Солоу является эффективность труда. Объяснение различий в уровне жизни разной эффективностью труда не требует огромных различий в капиталовооруженностях или ставках процента. В частности, на траектории сбалансированного роста капитал растет с тем же темпом, что и выпуск, а предельная отдача от капитала Однако эффективность труда в модели Солоу представлена весьма неполным образом. Наиболее очевидный недостаток состоит в том, что рост эффективности задается экзогенно: в модели постулируется поведение переменной, которая идентифицируется как источник роста. Не будет большим преувеличением сказать, что мы моделируем рост, просто предполагая его. Более фундаментальный дефект модели заключается в том, что она не уточняет понятие «эффективности труда»; модель подразумевает, что в этот показатель входит всё, что помимо труда и капитала воздействует на выпуск. Чтобы продвинуться далее в нашем анализе, мы должны понять, что означает сам термин «эффективность труда» и что обуславливает его изменение. Одной из естественных гипотез было бы предположение о том, что эффективность труда соответствует абстрактным знаниям. Тогда для объяснения мирового роста требуется выявить факторы, воздействующие на динамику запаса знаний. Для объяснения межстрановых различий в реальных доходах требуется понять, почему в одних странах фирмы имеют доступ к большему запасу знаний, чем в других, и почему эти знания не перетекают в бедные страны. Существуют другие интерпретация коэффициента Другой способ продвинуться в анализе роста – предположить, что роль капитала более значительна, чем предполагает модель Солоу. Если понятие «капитал» включает в себя не только физический капитал, или если с физическим капиталом связаны положительные внешние эффекты, то рыночная цена капитала будет плохим индикатором для оценки вклада капитала в выпуск. В этом случае, приведенные выше численные оценки могут быть неверными, а значит, не исключено, что различия в доходах объясняются различиями в капиталовооруженности. Возможные ответы на основные вопросы теории роста являются предметом изучения в главе 3.
Эмпирические приложения Калькуляция роста В модели Солоу, долгосрочные темпы роста выпуска на одного работника зависят только от темпов технического прогресса. Однако в краткосрочной перспективе рост может возникнуть как за счет технического прогресса, так и за счет накопления капитала. Следовательно, из модели Солоу следует, что определение источников краткосрочного роста является эмпирической проблемой. Калькуляция роста, разработанная Абрамовичем (Abramovitz, 1956) и Солоу (Solow, 1957)– это один из возможных способов анализа данного вопроса. Чтобы понять, как работает калькуляция роста, вернемся к производственной функции
Производные
Где
Темпы роста Изложенная базовая схема может быть обобщена многими способами (см., например, Денисона, (Dennis, 1967)). Наиболее распространенные модификации заключаются в том, чтобы рассмотреть различные виды капитала и труда, а также учесть изменение качества факторов. Возможны также более сложные модификации. Так, если есть подтверждения несовершенства конкуренции, то можно откорректировать данные о долях дохода, чтобы получить более точные оценки эластичности выпуска по различным факторам. Калькуляция роста используется для анализа широкого круга вопросов. Так, этот метод сыграл важную роль в недавних дебатах относительно исключительно высоких темпов роста новейших индустриальных стран Восточной Азии. Юнг (Young, 1995) на основе детальной калькуляции роста показал, что высокие темпы роста в этих странах по отношению к среднемировым темпам роста практически полностью обусловлены более высокими инвестициями, увеличением вовлеченности рабочей силы, улучшением качества труда (уровня образования), а не быстрым техническим прогрессом или другими факторами, воздействующими на остаток Солоу. Позже Исиех (Ysieh, 1998a) провел калькуляцию роста на основе анализа предельной отдачи факторов, а не количества факторов. Так, если высокие темпы роста обусловлены лишь накоплением капитала, то будет наблюдаться либо значительное снижение отдачи от капитала, либо значительный рост доли дохода капитала (или и то, и другое одновременно). Проведя калькуляцию роста таким образом, Хсиех пришел к выводу о значительно большей роли остатка. Другой пример. Калькуляция роста интенсивно использовалась для изучения причин замедления роста производительности, обусловившего снижение темпов роста душевого выпуска в Соединенных Штатах и других индустриальных странах в начале 1970-ых годов (см., например, Денисон (Denison, 1985), Бейли и Гордон (Baily and Gordon, 1988); Грилихес (Griliches, 1988); Джоргенсон (Jorgenson, 1988)). Проведенный анализ позволил выдвинуть в качестве объяснений ряд гипотез, основанных на замедлении роста квалификации рабочих, негативных последствиях повышения цен на нефть в 1970-х, снижении интенсивности инновационной активности, а также на негативных последствиях государственного вмешательства. В середине 1990-ых темпы роста производительности в США вернулись к тому уровню, на котором они находились до 1970-х годов. Калькуляция роста была использована также и для анализа этого периода (см. Олинер и Сичел (Olinger and Sichel, 2000), Джоргенсон и Стирох (Jorgenson and Stiroh 2000), Уелан (Whelan, 2000)). Эти исследования показывают, что основной причиной восстановления темпов роста было использование вычислительной техники и других информационных технологий. До середины 1990-ых быстрый технический прогресс в производстве компьютеров и их широкое внедрение оказывало лишь незначительное влияние на общую производительность. Однако в последующие годы это влияние было значительным. Поскольку использование вычислительной техники по прежнему расширяется, наш анализ показывает, что быстрый темп роста производительности конца 1990-ых, вероятно, продержится ещё, как минимум, несколько лет. Однако даже в этом мы не можем быть уверены полностью, и вряд ли сейчас можно предсказать, сколь долго будут наблюдаться высокие темпы роста. Конвергенция Вопрос, которому уделяется повышенное внимание в эмпирических исследованиях, заключается в следующем: существует ли тенденция к более быстрому росту бедной экономики, чем богатой? Существуют как минимум три причины для того, чтобы ожидать подобный эффект. Во-первых, модель Солоу предсказывает, что экономики стран стремятся к траекториям сбалансированного роста. А раз так, то в ситуации, когда разница в выпуске на одного работника между странами объясняется различиями в положении относительно траектории сбалансированного роста, следует ожидать, что бедные страны будут догонять богатых. Во-вторых, из модели Солоу следует, что предельная отдача от капитала ниже в странах с более высокой капиталовооруженностью. Следовательно, возникают стимулы для перетока капитала из богатых стран в бедные. В третьих, при существовании временных лагов в диффузии знаний, различия в доходах могут возникнуть в результате того, что некоторые страны ещё не начали использовать наиболее передовые технологии. Эти различия могут снизиться, если бедные страны получат к ним доступ. Баумоль (Baumol, 1986) на основе данных Мэдисона (Maddison, 1982) проверил гипотезу о наличии конвергенции между 16 индустриально развитыми странами на отрезке времени с 1870 по 1979 годы. В качестве объясняемой переменной использовался рост среднедушевого дохода за рассматриваемый период, а в качестве объясняющей – среднедушевой доход в начале периода. Он оценил следующую регрессию:
где Результаты выглядят следующим образом:
где число в скобках, 0,094, показывает стандартную ошибку коэффициента регрессии. На рисунке 1.7 представлен график, соответствующий этой регрессии. Рисунок 1.7. Начальный доход и последующие темпы роста в выборке Баумоля (источник: De Long, 1988. Использовано с разрешения автора). Если верить регрессии, то мы наблюдаем почти совершенную конвергенцию. Оцененное значение Однако Де Лонг (De Long, 1998) показал, что найденная Баумолем зависимость скорее всего является иллюзорной. Существуют две трудности. Во-первых, это проблема выборки. В связи с тем, что данные построены на основе исторической ретроспективы, достаточно длинные ряды данных имеются только для наиболее богатых стран. Страны, которые не были богатыми 100 лет назад, обычно оказываются в выборке, только если на протяжении этих 100 лет они демонстрировали достаточно высокие темпы роста. В противоположность этому, страны, которые 100 лет назад были богатыми, как правило, попадают в выборку, даже если они росли относительно медленно. В полученной таким образом выборке мы, вероятно, обнаружим, что бедные страны росли быстрее богатых, даже если в среднем подобной тенденции не существует. Для того, чтобы избежать смещенности оценок, можно использовать какое-нибудь правило построения выборки, не связанное с темпом роста в 1870-1979 годах, который мы пытаемся объяснить. Весь мир нельзя включить в выборку из-за нехватки данных. Поэтому Де Лонг включает в выборку страны, наиболее богатые в 1870 году; более точно, он включает все страны, которые в 1870 году были не менее богатыми, чем Финляндия – предпоследняя по уровню богатства страна в 1870 году в выборке Баумоля. Таким образом, Де Лонг включил в выборку Аргентину, Чили, Восточную Германию, Ирландию, Новую Зеландию, Португалию и Испанию, а исключенной из выборки оказалась Япония[22]. На рисунке 1.8 показан график рассеяния несмещенной выборки. Включение в выборку новых стран делает менее убедительной гипотезу о конвергенции. Теперь регрессия дает оценку параметра Вторая трудность, отмеченная Де Лонгом, это ошибки измерения. Оценки реального среднедушевого дохода в 1870 году не являются точными. Ошибки измерения также приводят к более высоким оценкам конвергенции. Если доход в 1870 году переоценен, то темпы роста с 1870 по 1979 год недооценены на соответствующую величину, а если недооценен, то темпы роста переоценены. Следовательно, оцененные темпы роста окажутся более высокими в странах с менее высоким начальным доходом, даже если не существует связи между темпом роста и начальным доходом. Де Лонг рассматривает следующую модель:
где К сожалению, невозможно оценить эту модель, основываясь только на данных о Тем не менее, как замечает Де Лонг, мы можем дать грубую оценку качества данных 1870 года, и таким образом получить разумную оценку стандартного отклонения ошибки. Например, гипотеза Даже сравнительно небольшая ошибка измерения оказывает значительное воздействие на результаты. Для несмещенной выборки, Можно также проверить гипотезу о конвергенции для различных выборок стран и различных периодов времени. На рисунке 1.9 представлена диаграмма рассеяния, аналогичная диаграммам на Рис. 1.7 и 1.8, построенная на основе выборки, включающей почти все некоммунистические страны мира для периода 1960- 1989 гг. Признаков конвергенции на данном рисунке не наблюдается. Мы вернемся к анализу данного вопроса в разделе 3.12. Рисунок 1.9. Начальный доход и последующий рост в послевоенный период.
Сбережения и инвестиции. Рассмотрим мир, в котором каждая страна описывается моделью Солоу, и все страны имеют одинаковую капиталовооруженность эффективного труда. Теперь предположим, что норма сбережений в одной из стран увеличивается. Если дополнительные сбережения инвестируются внутри страны, то предельная производительность капитала снизится и станет ниже, чем в других странах. В этом случае, у инвесторов рассматриваемой страны возникнет стимул к инвестированию за рубеж. Следовательно, если нет препятствий для потоков капитала, далеко не все новые сбережения будут инвестированы внутри страны. Напротив, дополнительные сбережения будут равномерно распределены по всему миру. Это означает, что рост сбережений в какой-либо стране не оказывает специфического влияния на инвестиции именно в этой стране. Следовательно, при отсутствии препятствий для мобильности капитала, нет причин ожидать, что в странах с высокой нормой сбережений будет наблюдаться высокая норма инвестиций. Фелдштейн и Хориока (Feldstein and Horioka1980) исследовали зависимость между нормой сбережений и нормой инвестиций. Они обнаружили, что, несмотря на приведенную аргументацию, сбережения и инвестиции сильно коррелируют друг с другом. Фелдштейн и Хориока оценили межстрановую регрессию на основе данных о средних нормах сбережений и инвестиций с 1960 по 1974 год в 21 индустриальной стране и получили следующие результаты:
где цифры в скобках, как и ра
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.239.50 (0.01 с.) |

 (1.21)
(1.21) - выпуск на единицу эффективного труда на траектории сбалансированного роста. Следовательно, для того, чтобы найти
- выпуск на единицу эффективного труда на траектории сбалансированного роста. Следовательно, для того, чтобы найти  , нам потребуется определить
, нам потребуется определить  . Для этого заметим, что
. Для этого заметим, что  задается условием
задается условием  , поэтому
, поэтому  (1.22)
(1.22) (и для любых значений
(и для любых значений 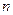 ,
,  , и
, и 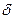 ). Следовательно, производные левой и правой частей по
). Следовательно, производные левой и правой частей по  (1.23)
(1.23) (1.24)
(1.24) (1.25)
(1.25) , чтобы слева получить эластичность
, чтобы слева получить эластичность  по
по  выразим
выразим  (1.26)
(1.26) – это эластичность выпуска по капиталу в точке
– это эластичность выпуска по капиталу в точке 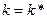 . Обозначив этот показатель через
. Обозначив этот показатель через  , имеем
, имеем (1.27)
(1.27) . Следовательно, если цена капитала равна его предельному продукту, то доля капитала (т.е., доля совокупного дохода, поступающая владельцам капитала) на траектории сбалансированного роста, равна
. Следовательно, если цена капитала равна его предельному продукту, то доля капитала (т.е., доля совокупного дохода, поступающая владельцам капитала) на траектории сбалансированного роста, равна  , то есть
, то есть  достаточно сильно вогнута. Поэтому при её сдвиге вверх точка её пересечения с кривой восстанавливающих инвестиций смещается на сравнительно небольшое расстояние, то есть, воздействие
достаточно сильно вогнута. Поэтому при её сдвиге вверх точка её пересечения с кривой восстанавливающих инвестиций смещается на сравнительно небольшое расстояние, то есть, воздействие  , а не
, а не  . Наша задача - определить, насколько быстро
. Наша задача - определить, насколько быстро 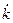 определяется величиной
определяется величиной  (см. (1.18)). Поэтому можно считать, что
(см. (1.18)). Поэтому можно считать, что  . Если
. Если  в окрестности точки
в окрестности точки  (1.28)
(1.28) величину
величину  . Тогда (1.28) принимает следующий вид:
. Тогда (1.28) принимает следующий вид: (1.29)
(1.29) отрицательно. Следовательно,
отрицательно. Следовательно,  примерно постоянен и равен
примерно постоянен и равен  . Отсюда вытекает, что
. Отсюда вытекает, что (1.30)
(1.30) – начальное значение
– начальное значение  (1.31)
(1.31) . Кроме того, можно показать, что
. Кроме того, можно показать, что  .
. составляет примерно 6 процентов в год (например, темпы роста населения могут составлять один-два процента, темпы роста производительности - также один-два процента, а норма амортизации - 3-4 процента). Если доля капитала в совокупном доходе равна одной трети, то
составляет примерно 6 процентов в год (например, темпы роста населения могут составлять один-два процента, темпы роста производительности - также один-два процента, а норма амортизации - 3-4 процента). Если доля капитала в совокупном доходе равна одной трети, то 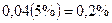 выше своей старой траектории через 1 год, на
выше своей старой траектории через 1 год, на  - через 18 лет и асимптотически стремится к траектории, расположенной выше старой на 5%. Таким образом, даже влияние значительного изменения нормы сбережений сравнительно невелико и реализуется не слишком быстро.[18]
- через 18 лет и асимптотически стремится к траектории, расположенной выше старой на 5%. Таким образом, даже влияние значительного изменения нормы сбережений сравнительно невелико и реализуется не слишком быстро.[18] и различия в эффективности труда
и различия в эффективности труда  . При этом мы показали, что только увеличение темпов роста эффективности труда может привести к перманентному увеличению темпов роста выпуска на одного работника и что для правдоподобных значений параметров влияние капиталовооруженности на среднедушевой выпуск невелико. Следовательно, только различия в эффективности труда дают возможность объяснить огромные различия уровней богатства во времени и в пространстве. Основной вывод из модели Солоу может быть сформулирован следующим образом: если доход, который капитал получает на рынке, соответствует его вкладу в производство, то значительную часть мирового экономического роста, равно как и значительную часть различий в доходах между странами, нельзя объяснить вариациями в накоплении физического капитала.
. При этом мы показали, что только увеличение темпов роста эффективности труда может привести к перманентному увеличению темпов роста выпуска на одного работника и что для правдоподобных значений параметров влияние капиталовооруженности на среднедушевой выпуск невелико. Следовательно, только различия в эффективности труда дают возможность объяснить огромные различия уровней богатства во времени и в пространстве. Основной вывод из модели Солоу может быть сформулирован следующим образом: если доход, который капитал получает на рынке, соответствует его вкладу в производство, то значительную часть мирового экономического роста, равно как и значительную часть различий в доходах между странами, нельзя объяснить вариациями в накоплении физического капитала. раз разницей в капиталовооруженности между рассматриваемыми странами. Если душевые выпуски различаются в
раз разницей в капиталовооруженности между рассматриваемыми странами. Если душевые выпуски различаются в 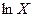 . Так как эластичность душевого выпуска по капиталовооруженности равна
. Так как эластичность душевого выпуска по капиталовооруженности равна  , разность между логарифмами капиталовооруженности должна составлять
, разность между логарифмами капиталовооруженности должна составлять  . Следовательно, капиталовооруженности различаются в
. Следовательно, капиталовооруженности различаются в  , или в
, или в  раз*.
раз*.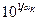 раз. Принимая
раз. Принимая  , получаем отношение капиталовооруженностей, равное
, получаем отношение капиталовооруженностей, равное  . Даже если капитал получает половину дохода, что значительно выше эмпирических наблюдений, капиталовооруженности должны различаться в
. Даже если капитал получает половину дохода, что значительно выше эмпирических наблюдений, капиталовооруженности должны различаться в  раз.
раз.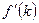 за вычетом нормы амортизации
за вычетом нормы амортизации  . Эластичность выпуска по капиталу в этом случае равна
. Эластичность выпуска по капиталу в этом случае равна  . Предельная отдача от капитала находится следующим образом:
. Предельная отдача от капитала находится следующим образом: (1.32)
(1.32) . Если
. Если  , то десятикратное различие в выпуске на одного работника, вытекающее из различий в капиталовооруженностях, подразумевает стократное различие в предельных отдачах от капитала. Так как ставка процента равна
, то десятикратное различие в выпуске на одного работника, вытекающее из различий в капиталовооруженностях, подразумевает стократное различие в предельных отдачах от капитала. Так как ставка процента равна  , то различия в ставках процента должны быть ещё больше.
, то различия в ставках процента должны быть ещё больше.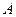 : образование и квалификация рабочей силы, гарантии прав собственности, качество инфраструктуры, отношение к предпринимательству и работе, определяющееся особенностями культуры, и т.д. Или же
: образование и квалификация рабочей силы, гарантии прав собственности, качество инфраструктуры, отношение к предпринимательству и работе, определяющееся особенностями культуры, и т.д. Или же  . Имеем:
. Имеем: (1.33)
(1.33) и
и  равны, соответственно,
равны, соответственно,  и
и  . Разделив обе части на
. Разделив обе части на  , получаем:
, получаем: (1.34)
(1.34) – эластичность выпуска по труду в момент
– эластичность выпуска по труду в момент  ,
,  – эластичность выпуска по капиталу, а
– эластичность выпуска по капиталу, а  . Вычитая из обеих частей
. Вычитая из обеих частей  , и используя свойство постоянной отдачи от масштаба,
, и используя свойство постоянной отдачи от масштаба,  (см. задачу 1.9), получаем выражение для темпа роста выпуска на одного работника:
(см. задачу 1.9), получаем выражение для темпа роста выпуска на одного работника: (1.35)
(1.35) ,
, 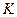 и
и 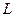 имеются в статистической отчетности. Мы знаем, что если цена капитала определяется его предельной производительностью, то
имеются в статистической отчетности. Мы знаем, что если цена капитала определяется его предельной производительностью, то  можно измерить как остаток в выражении (1.35). Таким образом, выражение (1.35) предлагает способ декомпозиции роста душевого дохода на сумму двух слагаемых: члена, зависящего от роста капиталовооруженности, и слагаемого
можно измерить как остаток в выражении (1.35). Таким образом, выражение (1.35) предлагает способ декомпозиции роста душевого дохода на сумму двух слагаемых: члена, зависящего от роста капиталовооруженности, и слагаемого  (1.36)
(1.36) – логарифм выпуска на работника,
– логарифм выпуска на работника,  – ошибка,
– ошибка, 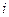 – номер страны[21]. Если конвергенция имеет место, то коэффициент
– номер страны[21]. Если конвергенция имеет место, то коэффициент  будет отрицательным: страны с более высокими начальными среднедушевыми доходами растут медленнее. Если
будет отрицательным: страны с более высокими начальными среднедушевыми доходами растут медленнее. Если  , то мы наблюдаем совершенную конвергенцию: более высокий начальный среднедушевой доход приводит к снижению последующих темпов роста в пропорции один к одному, а среднедушевой доход в 1979 году не коррелирует со среднедушевым доходом в 1870 году. Значение
, то мы наблюдаем совершенную конвергенцию: более высокий начальный среднедушевой доход приводит к снижению последующих темпов роста в пропорции один к одному, а среднедушевой доход в 1979 году не коррелирует со среднедушевым доходом в 1870 году. Значение  (1.37)
(1.37) , длина которого равна четырем стандартным ошибкам. Текущий доход на душу населения в данной выборке не коррелирует со среднедушевым доходом, имевшим место 100 лет назад.
, длина которого равна четырем стандартным ошибкам. Текущий доход на душу населения в данной выборке не коррелирует со среднедушевым доходом, имевшим место 100 лет назад. , со стандартной ошибкой
, со стандартной ошибкой  . Таким образом, учет смещенности выборки в процедуре Баумоля приводит к потере примерно половины обнаруженной конвергенции.
. Таким образом, учет смещенности выборки в процедуре Баумоля приводит к потере примерно половины обнаруженной конвергенции. , (1.38)
, (1.38) , (1.39)
, (1.39) – это истинное значение логарифма среднедушевого дохода в 1870 году, а
– это истинное значение логарифма среднедушевого дохода в 1870 году, а  – это измеренное значение. Предполагается, что
– это измеренное значение. Предполагается, что  не коррелируют друг с другом и с
не коррелируют друг с другом и с  и
и  . Проблема в том, что различные гипотезы приведут к одним и тем же наблюдаемым данным. Предположим, что мы обнаружили, что измеренный рост отрицательно зависит от начального дохода. Этот результат мы могли бы ожидать как в случае, когда ошибка измерения несущественна и конвергенция имеет место, так и в случае существенной ошибки и отсутствия конвергенции. В техническом смысле слова, модель является неидентифицируемой.
. Проблема в том, что различные гипотезы приведут к одним и тем же наблюдаемым данным. Предположим, что мы обнаружили, что измеренный рост отрицательно зависит от начального дохода. Этот результат мы могли бы ожидать как в случае, когда ошибка измерения несущественна и конвергенция имеет место, так и в случае существенной ошибки и отсутствия конвергенции. В техническом смысле слова, модель является неидентифицируемой. подразумевает, что мы измерили начальный доход со средней точностью в один процент; это неправдоподобно низкая оценка. Аналогично оценка
подразумевает, что мы измерили начальный доход со средней точностью в один процент; это неправдоподобно низкая оценка. Аналогично оценка  , предполагающая среднюю ошибку в 50%, кажется неправдоподобно высокой. Де Лонг показывает, что если мы зададим какое-то значение
, предполагающая среднюю ошибку в 50%, кажется неправдоподобно высокой. Де Лонг показывает, что если мы зададим какое-то значение  , мы сможем оценить остальные параметры.
, мы сможем оценить остальные параметры. (отсутствие тенденции к конвергенции) при
(отсутствие тенденции к конвергенции) при  , и значение
, и значение  (сильнейшая дивергенция) при
(сильнейшая дивергенция) при  . Следовательно, при правдоподобных значениях ошибки измерения результаты оценки конвергенции, проведенной Баумолем, почти полностью обесцениваются.
. Следовательно, при правдоподобных значениях ошибки измерения результаты оценки конвергенции, проведенной Баумолем, почти полностью обесцениваются. (1.40)
(1.40)


