

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Экономический рост: некоторые факты
Глава 1
Модель роста Роберта Солоу
Предположения
Факторы производства и выпуск
Модель Солоу концентрирует внимание на четырех переменных: выпуск  , капитал , капитал 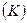 , труд , труд  и «знания», или «эффективность труда» и «знания», или «эффективность труда»  . В любой момент времени экономика располагает заданными объемами капитала, труда, и знаний, которые соединяются и создают выпуск. Производственная функция имеет следующий вид: . В любой момент времени экономика располагает заданными объемами капитала, труда, и знаний, которые соединяются и создают выпуск. Производственная функция имеет следующий вид:
 , (1.1) , (1.1)
где  обозначает время. обозначает время.
Следует отметить две особенности производственной функции. Во-первых, время не входит непосредственно в производственную функцию, а только лишь через 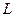 , , 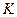 и и 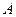 . Это означает, что выпуск меняется во времени только в том случае, если изменяется количество использованных ресурсов. Так, при заданных объемах капитала и труда, выпуск увеличивается во времени, только если увеличивается объем знаний (т.е. благодаря техническому прогрессу). . Это означает, что выпуск меняется во времени только в том случае, если изменяется количество использованных ресурсов. Так, при заданных объемах капитала и труда, выпуск увеличивается во времени, только если увеличивается объем знаний (т.е. благодаря техническому прогрессу).
Во-вторых, 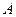 и и 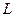 входят мультипликативно. Произведение входят мультипликативно. Произведение 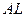 называют эффективным трудом, а технический прогресс, который данным способом входит в производственную функцию, называют воплощенным в труде, или нейтральным по Харроду [5]. Такой способ введения параметра называют эффективным трудом, а технический прогресс, который данным способом входит в производственную функцию, называют воплощенным в труде, или нейтральным по Харроду [5]. Такой способ введения параметра 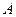 вместе с другими предположениями модели подразумевает, что отношение вместе с другими предположениями модели подразумевает, что отношение  в долгосрочной перспективе стабилизируется на каком-то уровне. На практике отношение капитала к выпуску не имеет явно выраженной тенденции к увеличению или уменьшению. К тому же, построив модель так, чтобы это отношение в долгосрочной перспективе становилось постоянным, мы значительно упрощаем анализ. Поэтому предположение о том, что в долгосрочной перспективе стабилизируется на каком-то уровне. На практике отношение капитала к выпуску не имеет явно выраженной тенденции к увеличению или уменьшению. К тому же, построив модель так, чтобы это отношение в долгосрочной перспективе становилось постоянным, мы значительно упрощаем анализ. Поэтому предположение о том, что 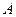 умножается на умножается на 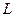 , является очень удобным. , является очень удобным.
Основные предположения модели Солоу касаются свойств производственной функции и эволюции трех факторов производства (капитала, труда и знаний). Перейдем к рассмотрению этих предположений.
Рисунок 1.1 Пример производственной функции
В качестве примера производственной функции часто используется функция Кобба-Дугласа,
 , ,  . (1.5) . (1.5)
Эту производственную функцию легко анализировать. Кроме того, она оказывается хорошим первым приближением для реальных производственных функций. Поэтому она очень полезна.
Легко проверить, что функция Кобба-Дугласа обладает постоянной отдачей от масштаба. Умножая факторы производства на  , получаем: , получаем:
 (1.6) (1.6)
Для того, чтобы получить производственную функцию в интенсивной форме, разделим оба фактора производства на 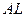 . Имеем: . Имеем:
 (1.7) (1.7)
Из уравнения (1.7) следует, что  . Непосредственно проверяется, что эта функция положительна, стремится к нулю, если . Непосредственно проверяется, что эта функция положительна, стремится к нулю, если  стремится к бесконечности, и стремится к бесконечности, если стремится к бесконечности, и стремится к бесконечности, если  стремится к нулю. Кроме того, вторая производная стремится к нулю. Кроме того, вторая производная  отрицательна[7]. отрицательна[7].
Динамика модели
Теперь мы хотим определить поведение только что описанной экономики. Эволюция двух из трех факторов производства, – труда и знаний, – задается экзогенно. Следовательно, чтобы определить поведение экономики, мы должны проанализировать поведение третьего фактора, капитала.
Динамика 
Ввиду того, что экономика со временем растет, оказывается значительно проще сосредоточиться на анализе динамики капиталовооруженности эффективного труда  , чем на динамике запаса капитала , чем на динамике запаса капитала 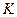 . Так как . Так как 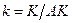 , мы можем применить правило дифференцирования дроби: , мы можем применить правило дифференцирования дроби:
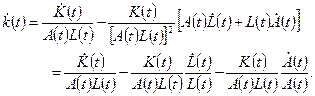 (1.16) (1.16)
Выражение 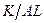 - это просто - это просто  . Согласно (1.8) и (1.9), . Согласно (1.8) и (1.9), 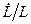 и и 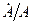 равны, соответственно, равны, соответственно, 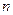 и и  . Величину . Величину  находим из (1.15). Подставив эти выражения в (1.16), получим: находим из (1.15). Подставив эти выражения в (1.16), получим:
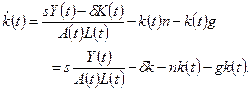 (1.17) (1.17)
Учитывая, что 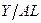 равно равно 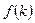 , имеем: , имеем:
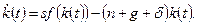 (1.18) (1.18)
Выражение (1.18) является основным уравнением динамики модели Солоу. Оно показывает, что изменение капиталовооруженности эффективного труда во времени определяется двумя слагаемыми. Первое слагаемое 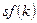 – это фактические инвестиции на единицу эффективного труда. Второе слагаемое – это фактические инвестиции на единицу эффективного труда. Второе слагаемое 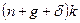 – это восстанавливающие инвестиции, т.е. объем инвестиций, который должен быть произведен, чтобы удержать – это восстанавливающие инвестиции, т.е. объем инвестиций, который должен быть произведен, чтобы удержать  на существующем уровне. Имеются две причины, по которым необходим некоторый объем инвестиций для удержания на существующем уровне. Имеются две причины, по которым необходим некоторый объем инвестиций для удержания  на постоянном уровне. Во-первых, существующий капитал амортизируется; поэтому для поддержания на заданном уровне его объема, капитал должен обновляться. Это объясняет роль слагаемого на постоянном уровне. Во-первых, существующий капитал амортизируется; поэтому для поддержания на заданном уровне его объема, капитал должен обновляться. Это объясняет роль слагаемого 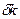 в выражении (1.18). Во-вторых, количество эффективного труда растет. Поэтому инвестиции, достаточные для поддержания на заданном уровне запаса капитала в выражении (1.18). Во-вторых, количество эффективного труда растет. Поэтому инвестиции, достаточные для поддержания на заданном уровне запаса капитала  недостаточны для того, чтобы поддерживать на заданном уровне капиталовооруженность эффективного труда недостаточны для того, чтобы поддерживать на заданном уровне капиталовооруженность эффективного труда 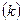 . Эффективный труд растет с темпом . Эффективный труд растет с темпом  , следовательно, чтобы оставить неизменным , следовательно, чтобы оставить неизменным  , запас капитала также должен расти с темпом , запас капитала также должен расти с темпом  .[10] Это объясняет роль слагаемого .[10] Это объясняет роль слагаемого 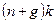 в выражении (1.18). в выражении (1.18).
Если фактические инвестиции на единицу эффективного труда превышают восстанавливающие инвестиции, то  растет. Если фактические инвестиции на единицу эффективного труда меньше восстанавливающих инвестиций, то растет. Если фактические инвестиции на единицу эффективного труда меньше восстанавливающих инвестиций, то  падает. А когда они равны между собой, переменная падает. А когда они равны между собой, переменная  постоянна во времени. постоянна во времени.
Рисунок 1.2 Фактические и восстанавливающие инвестиции
На рисунке 1.2 изображена зависимость рассмотренных двух слагаемых, задающих 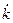 , как функций от , как функций от  . Восстанавливающие инвестиции . Восстанавливающие инвестиции 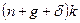 пропорциональны пропорциональны  . Фактические инвестиции . Фактические инвестиции 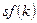 – это константа, умноженная на выпуск на единицу эффективного труда. – это константа, умноженная на выпуск на единицу эффективного труда.
Так как 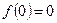 , фактические инвестиции равны восстанавливающим в точке , фактические инвестиции равны восстанавливающим в точке 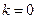 . Из условий Инады следует, что при . Из условий Инады следует, что при 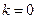 производная производная 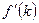 велика, т.е., кривая велика, т.е., кривая 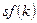 имеет более крутой наклон, чем прямая имеет более крутой наклон, чем прямая 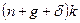 . Поэтому при маленьких значениях . Поэтому при маленьких значениях  фактические инвестиции превышают восстанавливающие. Из условия Инады также следует, что фактические инвестиции превышают восстанавливающие. Из условия Инады также следует, что 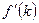 стремится к нулю с увеличением стремится к нулю с увеличением  . Значит, в некоторой точке наклон кривой фактических инвестиций оказывается меньше наклона прямой восстанавливающих инвестиций. Следовательно, эти линии должны где-то пересечься. Наконец, условие . Значит, в некоторой точке наклон кривой фактических инвестиций оказывается меньше наклона прямой восстанавливающих инвестиций. Следовательно, эти линии должны где-то пересечься. Наконец, условие 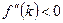 гарантирует, что для гарантирует, что для 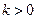 эти линии пересекаются только один раз. Обозначим через эти линии пересекаются только один раз. Обозначим через  - значение - значение  в той самой точке, где фактические инвестиции равны восстанавливающим. в той самой точке, где фактические инвестиции равны восстанавливающим.
Рисунок 1.3 Фазовая диаграмма для  в модели Солоу. в модели Солоу.
Рисунок 1.3 обобщает полученную информацию посредством фазовой диаграммы, на которой отражена зависимость 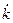 от от  . Если в начальный момент времени . Если в начальный момент времени  меньше, чем меньше, чем  , то фактические инвестиции больше восстанавливающих, , то фактические инвестиции больше восстанавливающих, 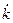 положительна, и положительна, и  растет. Если растет. Если  больше больше  , то , то 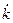 отрицательна. Если отрицательна. Если  равно равно  , то , то  . Следовательно, независимо от начального значения, . Следовательно, независимо от начального значения,  стремится к стремится к  .[11] .[11]
Влияние на выпуск
Увеличение  сдвигает кривую фактических инвестиций вверх, и сдвигает кривую фактических инвестиций вверх, и  увеличивается. Это показано на рисунке 1.4. Однако увеличивается. Это показано на рисунке 1.4. Однако  не мгновенно принимает свое новое значение не мгновенно принимает свое новое значение  . Изначально . Изначально  равно старому значению равно старому значению  . В этой точке фактические инвестиции теперь превышают восстанавливающие: инвестируется больше ресурсов, чем требуется для поддержания . В этой точке фактические инвестиции теперь превышают восстанавливающие: инвестируется больше ресурсов, чем требуется для поддержания  на постоянном уровне, значит, на постоянном уровне, значит, 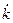 – положительно. Следовательно, капиталовооруженность эффективного труда – положительно. Следовательно, капиталовооруженность эффективного труда  начинает расти и продолжает рост до тех пор, пока не достигнет нового значения начинает расти и продолжает рост до тех пор, пока не достигнет нового значения  , при котором она остается постоянной*. , при котором она остается постоянной*.
Рисунок 1.4 Воздействие нормы сбережений на фактические инвестиции.
Эти рассуждения отражены на первых трех графиках рисунка 1.5. 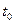 – это момент времени, когда происходит увеличение нормы сбережений. Мы предположили, что – это момент времени, когда происходит увеличение нормы сбережений. Мы предположили, что  увеличивается в момент увеличивается в момент 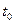 , а затем остается постоянной. Так как скачек , а затем остается постоянной. Так как скачек  приводит к тому, что фактические инвестиции превышают восстанавливающие на какую-то строго положительную величину, приводит к тому, что фактические инвестиции превышают восстанавливающие на какую-то строго положительную величину, 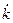 меняется скачком с нуля до какого-то строго положительного значения. Переменная меняется скачком с нуля до какого-то строго положительного значения. Переменная  плавно увеличивается со старого до нового значения плавно увеличивается со старого до нового значения  , а , а 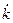 плавно снижается до нуля[13]. плавно снижается до нуля[13].
Рисунок 1.5. Результаты увеличения нормы сбережений.
Особый интерес для нас представляет динамика выпуска на одного работника,  . Величина . Величина  равна равна  . Если . Если  постоянна, то постоянна, то  растет с темпом растет с темпом  , т.е. с темпом роста , т.е. с темпом роста 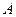 . Когда . Когда  увеличивается, увеличивается,  растет в результате роста и растет в результате роста и 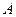 , и , и  . Следовательно, темпы роста . Следовательно, темпы роста  превышают темпы роста превышают темпы роста 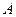 . Однако, когда . Однако, когда  достигает нового значения достигает нового значения  , вновь лишь рост , вновь лишь рост 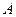 приводит к росту приводит к росту  , следовательно, темпы роста , следовательно, темпы роста  снова становятся равными снова становятся равными  . Таким образом, перманентное увеличение нормы сбережений приводит к временному увеличению темпов роста выпуска на одного работника: . Таким образом, перманентное увеличение нормы сбережений приводит к временному увеличению темпов роста выпуска на одного работника:  на некотором интервале времени увеличивается, но, в конце концов, достигает точки, в которой дополнительные сбережения идут только на то, чтобы поддерживать на некотором интервале времени увеличивается, но, в конце концов, достигает точки, в которой дополнительные сбережения идут только на то, чтобы поддерживать  на более высоком уровне. на более высоком уровне.
Четвертый и пятый график на рисунке 1.5. показывают, как сбережения влияют на динамику душевого выпуска. Темп роста выпуска на одного работника, изначально равный  , увеличивается скачком в момент , увеличивается скачком в момент 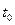 , а затем плавно возвращается на свой первоначальный уровень. Следовательно, выпуск на одного работника сначала увеличивается по сравнению с начальной траекторией, а затем стабилизируется на более высокой траектории, которая параллельна первоначальной[14]. , а затем плавно возвращается на свой первоначальный уровень. Следовательно, выпуск на одного работника сначала увеличивается по сравнению с начальной траекторией, а затем стабилизируется на более высокой траектории, которая параллельна первоначальной[14].
Таким образом, изменение нормы сбережений оказывает воздействие на уровень, но не воздействие на рост: это изменяет траекторию сбалансированного роста, а значит и выпуск на одного работника в любой момент времени, но не влияет на темпы роста выпуска на одного работника на траектории сбалансированного роста. На самом деле, в модели Солоу только изменение темпов технического прогресса оказывает воздействие на рост; любые другие изменения оказывают воздействие лишь на уровень.
(Лит. Редактору: «воздействие» - термин, не заменять. «Влияние» - другое слово. В.П.)
Влияние на потребление
Если бы мы ввели в модель домашние хозяйства, тогда их благосостояние зависело бы не от выпуска, а от потребления: инвестиции это лишь фактор производства в будущем. Следовательно, для анализа многих вопросов мы более заинтересованы в анализе динамики потребления, чем динамики выпуска.
Потребление на единицу эффективного труда равняется выпуску на единицу эффективного труда 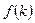 , умноженному на норму потребления , умноженному на норму потребления  . Так как . Так как  меняется скачком в момент меняется скачком в момент 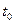 , а , а  - нет, потребление на единицу эффективного труда скачкообразно уменьшается. Затем потребление растет, так как растет - нет, потребление на единицу эффективного труда скачкообразно уменьшается. Затем потребление растет, так как растет  , а , а  остается на высоком уровне. Это показано на последнем графике рисунка 1.5. остается на высоком уровне. Это показано на последнем графике рисунка 1.5.
В общем случае не ясно, превысит ли потребление свой первоначальный уровень. Обозначим через  - потребление на единицу эффективного труда на траектории сбалансированного роста. Очевидно, - потребление на единицу эффективного труда на траектории сбалансированного роста. Очевидно,  равно выпуску на единицу эффективного труда, равно выпуску на единицу эффективного труда,  , за вычетом инвестиций на единицу эффективного труда, , за вычетом инвестиций на единицу эффективного труда,  . На траектории сбалансированного роста фактические инвестиции равняются восстанавливающим, . На траектории сбалансированного роста фактические инвестиции равняются восстанавливающим,  . Следовательно, . Следовательно,
 (1.19) (1.19)
Величина  задается нормой сбережений задается нормой сбережений  , а также другими параметрами модели: , а также другими параметрами модели: 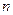 , ,  , и , и 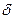 ; значит, мы можем записать ; значит, мы можем записать  . Тогда из выражения (1.19) получаем: . Тогда из выражения (1.19) получаем:
 (1.20) (1.20)
Мы знаем, что рост  приводит к увеличению приводит к увеличению  . Следовательно, в зависимости от того, больше или меньше предельная отдача от капитала . Следовательно, в зависимости от того, больше или меньше предельная отдача от капитала 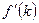 , чем , чем  , увеличение нормы сбережений может приводить как к увеличению, так и к уменьшению потребления в долгосрочной перспективе. Если , увеличение нормы сбережений может приводить как к увеличению, так и к уменьшению потребления в долгосрочной перспективе. Если  увеличивается, то для удержания увеличивается, то для удержания  на более высоком уровне следует увеличить инвестиции (на единицу эффективного труда) на величину на более высоком уровне следует увеличить инвестиции (на единицу эффективного труда) на величину  , умноженную на изменение , умноженную на изменение  . Если . Если 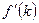 меньше, чем меньше, чем  , то приращения выпуска, достигнутого за счет роста капитала, недостаточно для того, чтобы удержать запас капитала на новом, более высоком уровне. В этом случае потребление должно снизиться, чтобы удержать более высокий запас капитала. Если , то приращения выпуска, достигнутого за счет роста капитала, недостаточно для того, чтобы удержать запас капитала на новом, более высоком уровне. В этом случае потребление должно снизиться, чтобы удержать более высокий запас капитала. Если  превышает превышает  , то приращение выпуска больше, чем требуется для удержания , то приращение выпуска больше, чем требуется для удержания  на новом уровне, и потребление увеличивается. на новом уровне, и потребление увеличивается.
Производная 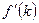 может быть больше или меньше, чем может быть больше или меньше, чем  . Это показано на рисунке 1.6. На рисунке изображены не только . Это показано на рисунке 1.6. На рисунке изображены не только 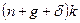 и и 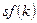 , но также и , но также и 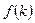 . На траектории сбалансированного роста потребление равно выпуску за вычетом восстанавливающих инвестиций; таким образом, . На траектории сбалансированного роста потребление равно выпуску за вычетом восстанавливающих инвестиций; таким образом,  определяется расстоянием между определяется расстоянием между 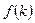 и и 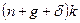 . На верхнем графике . На верхнем графике  меньше, чем меньше, чем 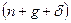 , поэтому увеличение нормы сбережений приводит к сокращению потребления даже когда экономика достигает новой траектории сбалансированного роста. На среднем графике наблюдается обратная картина, и увеличение , поэтому увеличение нормы сбережений приводит к сокращению потребления даже когда экономика достигает новой траектории сбалансированного роста. На среднем графике наблюдается обратная картина, и увеличение  приводит к росту потребления в долгосрочной перспективе. приводит к росту потребления в долгосрочной перспективе.
Рисунок 1.6. Выпуск, инвестиции и потребление на траектории сбалансированного роста.
На нижнем графике 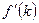 в точности равняется в точности равняется  : линии : линии 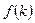 и и 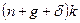 параллельны друг другу в точке параллельны друг другу в точке 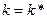 . В этом случае предельное изменение . В этом случае предельное изменение  не воздействует на потребление в долгосрочной перспективе, а потребление находится на уровне, максимальном среди всех возможных траекторий сбалансированного роста. Это значение не воздействует на потребление в долгосрочной перспективе, а потребление находится на уровне, максимальном среди всех возможных траекторий сбалансированного роста. Это значение  называется запасом капитала, соответствующим золотому правилу. Мы обсудим золотое правило накопления капитала в главе 2. В частности, мы ответим на вопрос, является ли запас капитала, соответствующий золотому правилу, желательным для экономики, и существуют ли ситуации, когда децентрализованная экономика с эндогенной нормой сбережения стремится к этому запасу. Разумеется, в модели Солоу, где норма сбережения экзогенна, не существует причин ожидать, что запас капитала на траектории сбалансированного роста будет соответствовать золотому правилу. называется запасом капитала, соответствующим золотому правилу. Мы обсудим золотое правило накопления капитала в главе 2. В частности, мы ответим на вопрос, является ли запас капитала, соответствующий золотому правилу, желательным для экономики, и существуют ли ситуации, когда децентрализованная экономика с эндогенной нормой сбережения стремится к этому запасу. Разумеется, в модели Солоу, где норма сбережения экзогенна, не существует причин ожидать, что запас капитала на траектории сбалансированного роста будет соответствовать золотому правилу.
Количественные оценки
Очень часто нас интересуют не только качественные выводы из рассматриваемой модели, но также и количественные оценки. Если, например, последствием небольшого воздействия на норму сбережений является значительное изменение темпов роста на протяжении нескольких столетий, то утверждение, что это воздействие является временным, не представляет особого интереса.
Для большинства моделей, включая модель Солоу, для получения точных численных оценок требуется выбрать конкретные функциональные формы и значения параметров; зачастую также требуется провести численный анализ модели. Однако во многих случаях многое можно понять, рассматривая аппроксимацию модели в окрестности долгосрочного равновесия. Этим подходом мы сейчас и воспользуемся.
Скорость сходимости
На практике нас интересует не только долгосрочный эффект некоторых воздействий (таких, как изменение нормы сбережений), но и насколько быстро этот эффект реализуется. Опять-таки, можно использовать аппроксимацию модели в окрестности точки долгосрочного равновесия, чтобы ответить на этот вопрос.
Для простоты сосредоточимся на поведении  , а не , а не  . Наша задача - определить, насколько быстро . Наша задача - определить, насколько быстро  приближается к приближается к  . Мы знаем, что значение . Мы знаем, что значение 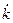 определяется величиной определяется величиной  : напомним, что ключевое уравнение модели имеет вид : напомним, что ключевое уравнение модели имеет вид  (см. (1.18)). Поэтому можно считать, что (см. (1.18)). Поэтому можно считать, что 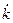 = =  . Если . Если  совпадает с совпадает с  , то , то 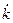 равно нулю. Следовательно, разложение в ряд Тейлора функции равно нулю. Следовательно, разложение в ряд Тейлора функции  в окрестности точки в окрестности точки 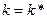 имеет вид имеет вид
 (1.28) (1.28)
То есть, 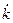 приблизительно равно произведению разности приблизительно равно произведению разности  и и  на производную от на производную от 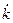 по по  в точке в точке 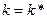 . .
Обозначим через  величину величину  . Тогда (1.28) принимает следующий вид: . Тогда (1.28) принимает следующий вид:
 (1.29) (1.29)
Так как 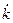 положительно, если положительно, если  немного меньше немного меньше  , и отрицательно, если , и отрицательно, если  немного больше немного больше  , то , то  отрицательно. Следовательно, отрицательно. Следовательно,  положительно. положительно.
Из уравнения (1.29) следует, что в окрестности траектории сбалансированного роста капиталовооруженность  стремится к значению стремится к значению  со скоростью, примерно пропорциональной её отклонению от со скоростью, примерно пропорциональной её отклонению от  . Значит, темп роста . Значит, темп роста  примерно постоянен и равен примерно постоянен и равен  . Отсюда вытекает, что . Отсюда вытекает, что
 (1.30) (1.30)
где  – начальное значение – начальное значение  . Заметим, что выражение (1.30) непосредственно следует из условия, что система устойчива и что мы линеаризуем выражение для . Заметим, что выражение (1.30) непосредственно следует из условия, что система устойчива и что мы линеаризуем выражение для 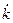 в окрестности точки в окрестности точки 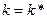 . .
Осталось определить  ; именно здесь используется специфика модели. Дифференцируя формулу (1.18), считая ; именно здесь используется специфика модели. Дифференцируя формулу (1.18), считая 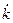 функцией от функцией от  , и оценивая результирующее выражение в точке , и оценивая результирующее выражение в точке 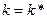 , получаем , получаем
 (1.31) (1.31)
где в третьей строчке мы использовали соотношение  , выразив из него , выразив из него  , а в последней строчке воспользовались определением , а в последней строчке воспользовались определением  . Следовательно, . Следовательно,  стремится к своему значению, соответствующему траектории сбалансированного роста, с темпом стремится к своему значению, соответствующему траектории сбалансированного роста, с темпом  . Кроме того, можно показать, что . Кроме того, можно показать, что  стремится к стремится к  с тем же темпом, что с тем же темпом, что  стремится к стремится к  . Следовательно, . Следовательно,  . .
Мы можем подобрать параметры (1.31), чтобы оценить, насколько быстро экономика стремится к траектории сбалансированного роста. Обычно  составляет примерно 6 процентов в год (например, темпы роста населения могут составлять один-два процента, темпы роста производительности - также один-два процента, а норма амортизации - 3-4 процента). Если доля капитала в совокупном доходе равна одной трети, то составляет примерно 6 процентов в год (например, темпы роста населения могут составлять один-два процента, темпы роста производительности - также один-два процента, а норма амортизации - 3-4 процента). Если доля капитала в совокупном доходе равна одной трети, то  составляет примерно 4 процента. Таким образом, расстояние между составляет примерно 4 процента. Таким образом, расстояние между  и и  , а также между , а также между  и и  каждый год сокращается примерно на 4 процента, и требуется примерно 18 лет для того, чтобы пройти половину пути до траектории сбалансированного роста.[17] Следовательно, в нашем примере при увеличении нормы сбережений на 10%, выпуск оказывается на каждый год сокращается примерно на 4 процента, и требуется примерно 18 лет для того, чтобы пройти половину пути до траектории сбалансированного роста.[17] Следовательно, в нашем примере при увеличении нормы сбережений на 10%, выпуск оказывается на 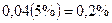 выше своей старой траектории через 1 год, на выше своей старой траектории через 1 год, на  - через 18 лет и асимптотически стремится к траектории, расположенной выше старой на 5%. Таким образом, даже влияние значительного изменения нормы сбережений сравнительно невелико и реализуется не слишком быстро.[18] - через 18 лет и асимптотически стремится к траектории, расположенной выше старой на 5%. Таким образом, даже влияние значительного изменения нормы сбережений сравнительно невелико и реализуется не слишком быстро.[18]
1.6 Модель Солоу и основные вопросы теории роста
Модель Солоу выявляет две возможные причины межвременных или межстрановых различий в уровнях душевого выпуска: различия в капиталовооруженности труда  и различия в эффективности труда и различия в эффективности труда  . При этом мы показали, что только увеличение темпов роста эффективности труда может привести к перманентному увеличению темпов роста выпуска на одного работника и что для правдоподобных значений параметров влияние капиталовооруженности на среднедушевой выпуск невелико. Следовательно, только различия в эффективности труда дают возможность объяснить огромные различия уровней богатства во времени и в пространстве. Основной вывод из модели Солоу может быть сформулирован следующим образом: если доход, который капитал получает на рынке, соответствует его вкладу в производство, то значительную часть мирового экономического роста, равно как и значительную часть различий в доходах между странами, нельзя объяснить вариациями в накоплении физического капитала. . При этом мы показали, что только увеличение темпов роста эффективности труда может привести к перманентному увеличению темпов роста выпуска на одного работника и что для правдоподобных значений параметров влияние капиталовооруженности на среднедушевой выпуск невелико. Следовательно, только различия в эффективности труда дают возможность объяснить огромные различия уровней богатства во времени и в пространстве. Основной вывод из модели Солоу может быть сформулирован следующим образом: если доход, который капитал получает на рынке, соответствует его вкладу в производство, то значительную часть мирового экономического роста, равно как и значительную часть различий в доходах между странами, нельзя объяснить вариациями в накоплении физического капитала.
Существуют два способа показать, почему из модели Солоу следует данный вывод: один способ прямой, другой – косвенный. Прямой подход – это оценка необходимых различий в капиталовооруженности. Предположим, что мы пытаемся объяснить межстрановое различие в выпуске на одного работника в  раз разницей в капиталовооруженности между рассматриваемыми странами. Если душевые выпуски различаются в раз разницей в капиталовооруженности между рассматриваемыми странами. Если душевые выпуски различаются в  раз, то разность между их логарифмами составляет раз, то разность между их логарифмами составляет 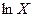 . Так как эластичность душевого выпуска по капиталовооруженности равна . Так как эластичность душевого выпуска по капиталовооруженности равна  , разность между логарифмами капиталовооруженности должна составлять , разность между логарифмами капиталовооруженности должна составлять  . Следовательно, капиталовооруженности различаются в . Следовательно, капиталовооруженности различаются в  , или в , или в  раз*. раз*.
Выпуск на одного работника в индустриальных странах за последние 100 лет вырос примерно в 10 раз; отношение выпуска в индустриальных странах к выпуску в беднейших странах имеет примерно такой же порядок. Следовательно, мы хотим объяснить значение переменной  , находящееся где-то в окрестности десяти. Наш анализ показывает, что если эти различия объясняются капиталовооруженностью труда, то капиталовооруженности должны различаться примерно в , находящееся где-то в окрестности десяти. Наш анализ показывает, что если эти различия объясняются капиталовооруженностью труда, то капиталовооруженности должны различаться примерно в 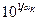 раз. Принимая раз. Принимая  , получаем отношение капиталовооруженностей, равное , получаем отношение капиталовооруженностей, равное  . Даже если капитал получает половину дохода, что значительно выше эмпирических наблюдений, капиталовооруженности должны различаться в . Даже если капитал получает половину дохода, что значительно выше эмпирических наблюдений, капиталовооруженности должны различаться в  раз. раз.
Эмпирические данные не подтверждают столь значительных различий в запасе капитала. Отношение капитала к выпуску приблизительно постоянно во времени. Следовательно, капиталовооруженность труда в индустриальных странах за последние 100 лет выросла примерно в 10 раз, а не в 100 и не в 1000 раз. Аналогично, межстрановые различия в капиталовооруженности хоть и значительны, но не столь велики. Например, отношение капитала к выпуску в индустриальных странах приблизительно в 2-3 раза больше этого отношения в бедных странах; следовательно, капиталовооруженности различаются «лишь» в 20-30 раз. Итак, различия в капиталовооруженности недостаточны для того, чтобы объяснить различия в доходах на одного работника, которые мы пытаемся понять[19].
Косвенный способ убедиться в неспособности модели объяснить значительные различия в выпуске на одного работника заключается в демонстрации того, что требуемые для объяснения различия в капиталовооруженности влекут за собой неправдоподобно большие различия в предельной отдаче от капитала (см. Лукас (Lucas, 1990)). Если рынки являются конкурентными, то ставка процента равна предельной производительности капитала 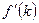 за вычетом нормы амортизации за вычетом нормы амортизации 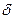 . Предположим, что производственная функция является функцией Кобба-Дугласа (см. выражение [1.5]), которая в интенсивной форме записывается как . Предположим, что производственная функция является функцией Кобба-Дугласа (см. выражение [1.5]), которая в интенсивной форме записывается как  . Эластичность выпуска по капиталу в этом случае равна . Эластичность выпуска по капиталу в этом случае равна  . Предельная отдача от капитала находится следующим образом: . Предельная отдача от капитала находится следующим образом:
 (1.32) (1.32)
Выражение (1.32) показывает, что эластичность предельной отдачи от капитала по выпуску равна  . Если . Если  , то десятикратное различие в выпуске на одного работника, вытекающее из различий в капиталовооруженностях, подразумевает стократное различие в предельных отдачах от капитала. Так как ставка процента равна , то десятикратное различие в выпуске на одного работника, вытекающее из различий в капиталовооруженностях, подразумевает стократное различие в предельных отдачах от капитала. Так как ставка процента равна  , то различия в ставках процента должны быть ещё больше. , то различия в ставках процента должны быть ещё больше.
Как и в случае с капиталовооруженностью, мы не наблюдаем таких различий в ставках процента. Прямые оценки отдачи от капитала на финансовых рынках показывают лишь незначительные вариации этого показателя во времени или между странами. Более показательными являются оценки межстрановых различий, построенные на основе анализа того, куда инвестируют владельцы капитала. Если бы ставка процента была в 10 или 100 раз выше в бедных странах, чем в богатых, то существовали бы огромные стимулы для того, чтобы инвестировать именно в бедные страны. При подобных различиях в предельной производительности капитала, влияние таких факторов, как несовершенство финансового рынка, налоговая политика, риск экспроприации, и т. д., отошло бы на второй план, и мы наблюдали бы мощный поток инвестиций из богатых стран в бедные. Мы не наблюдаем этих потоков[20].
Следовательно, если мы полагаем, что вклад капитала в выпуск примерно соответствует его рыночной цене, то мы не можем объяснить различий в выпуске на одного работника различиями в капиталовооруженности.
Другой возможной причиной различий выпуска на одного работника в модели Солоу является эффективность труда. Объяснение различий в уровне жизни разной эффективностью труда не требует огромных различий в капиталовооруженностях или ставках процента. В частности, на траектории сбалансированного роста капитал растет с тем же темпом, что и выпуск, а предельная отдача от капитала 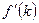 постоянна. постоянна.
Однако эффективность труда в модели Солоу представлена весьма неполным образом. Наиболее очевидный недостаток состоит в том, что рост эффективности задается экзогенно: в модели постулируется поведение переменной, которая идентифицируется как источник роста. Не будет большим преувеличением сказать, что мы моделируем рост, просто предполагая его.
Более фундаментальный дефект модели заключается в том, что она не уточняет понятие «эффективности труда»; модель подразумевает, что в этот показатель входит всё, что помимо труда и капитала воздействует на выпуск. Чтобы продвинуться далее в нашем анализе, мы должны понять, что означает сам термин «эффективность труда» и что обуславливает его изменение. Одной из естественных гипотез было бы предположение о том, что эффективность труда соответствует абстрактным знаниям. Тогда для объяснения мирового роста требуется выявить факторы, воздействующие на
|



 , капитал
, капитал 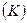 , труд
, труд  и «знания», или «эффективность труда»
и «знания», или «эффективность труда»  . В любой момент времени экономика располагает заданными объемами капитала, труда, и знаний, которые соединяются и создают выпуск. Производственная функция имеет следующий вид:
. В любой момент времени экономика располагает заданными объемами капитала, труда, и знаний, которые соединяются и создают выпуск. Производственная функция имеет следующий вид: , (1.1)
, (1.1) обозначает время.
обозначает время.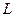 ,
, 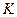 и
и 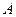 . Это означает, что выпуск меняется во времени только в том случае, если изменяется количество использованных ресурсов. Так, при заданных объемах капитала и труда, выпуск увеличивается во времени, только если увеличивается объем знаний (т.е. благодаря техническому прогрессу).
. Это означает, что выпуск меняется во времени только в том случае, если изменяется количество использованных ресурсов. Так, при заданных объемах капитала и труда, выпуск увеличивается во времени, только если увеличивается объем знаний (т.е. благодаря техническому прогрессу).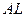 называют эффективным трудом, а технический прогресс, который данным способом входит в производственную функцию, называют воплощенным в труде, или нейтральным по Харроду [5]. Такой способ введения параметра
называют эффективным трудом, а технический прогресс, который данным способом входит в производственную функцию, называют воплощенным в труде, или нейтральным по Харроду [5]. Такой способ введения параметра  в долгосрочной перспективе стабилизируется на каком-то уровне. На практике отношение капитала к выпуску не имеет явно выраженной тенденции к увеличению или уменьшению. К тому же, построив модель так, чтобы это отношение в долгосрочной перспективе становилось постоянным, мы значительно упрощаем анализ. Поэтому предположение о том, что
в долгосрочной перспективе стабилизируется на каком-то уровне. На практике отношение капитала к выпуску не имеет явно выраженной тенденции к увеличению или уменьшению. К тому же, построив модель так, чтобы это отношение в долгосрочной перспективе становилось постоянным, мы значительно упрощаем анализ. Поэтому предположение о том, что  ,
,  . (1.5)
. (1.5) , получаем:
, получаем: (1.6)
(1.6) (1.7)
(1.7) . Непосредственно проверяется, что эта функция положительна, стремится к нулю, если
. Непосредственно проверяется, что эта функция положительна, стремится к нулю, если  стремится к бесконечности, и стремится к бесконечности, если
стремится к бесконечности, и стремится к бесконечности, если  отрицательна[7].
отрицательна[7].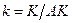 , мы можем применить правило дифференцирования дроби:
, мы можем применить правило дифференцирования дроби: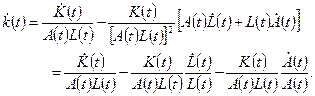 (1.16)
(1.16)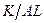 - это просто
- это просто 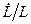 и
и 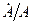 равны, соответственно,
равны, соответственно, 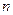 и
и  . Величину
. Величину  находим из (1.15). Подставив эти выражения в (1.16), получим:
находим из (1.15). Подставив эти выражения в (1.16), получим: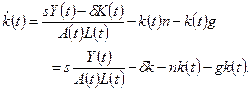 (1.17)
(1.17)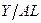 равно
равно 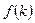 , имеем:
, имеем: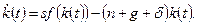 (1.18)
(1.18)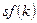 – это фактические инвестиции на единицу эффективного труда. Второе слагаемое
– это фактические инвестиции на единицу эффективного труда. Второе слагаемое 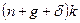 – это восстанавливающие инвестиции, т.е. объем инвестиций, который должен быть произведен, чтобы удержать
– это восстанавливающие инвестиции, т.е. объем инвестиций, который должен быть произведен, чтобы удержать 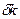 в выражении (1.18). Во-вторых, количество эффективного труда растет. Поэтому инвестиции, достаточные для поддержания на заданном уровне запаса капитала
в выражении (1.18). Во-вторых, количество эффективного труда растет. Поэтому инвестиции, достаточные для поддержания на заданном уровне запаса капитала  недостаточны для того, чтобы поддерживать на заданном уровне капиталовооруженность эффективного труда
недостаточны для того, чтобы поддерживать на заданном уровне капиталовооруженность эффективного труда 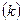 . Эффективный труд растет с темпом
. Эффективный труд растет с темпом  , следовательно, чтобы оставить неизменным
, следовательно, чтобы оставить неизменным 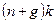 в выражении (1.18).
в выражении (1.18).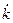 , как функций от
, как функций от 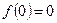 , фактические инвестиции равны восстанавливающим в точке
, фактические инвестиции равны восстанавливающим в точке 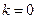 . Из условий Инады следует, что при
. Из условий Инады следует, что при 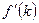 велика, т.е., кривая
велика, т.е., кривая 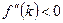 гарантирует, что для
гарантирует, что для 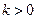 эти линии пересекаются только один раз. Обозначим через
эти линии пересекаются только один раз. Обозначим через  - значение
- значение  . Следовательно, независимо от начального значения,
. Следовательно, независимо от начального значения,  сдвигает кривую фактических инвестиций вверх, и
сдвигает кривую фактических инвестиций вверх, и 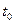 – это момент времени, когда происходит увеличение нормы сбережений. Мы предположили, что
– это момент времени, когда происходит увеличение нормы сбережений. Мы предположили, что  . Величина
. Величина  . Если
. Если 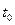 , а затем плавно возвращается на свой первоначальный уровень. Следовательно, выпуск на одного работника сначала увеличивается по сравнению с начальной траекторией, а затем стабилизируется на более высокой траектории, которая параллельна первоначальной[14].
, а затем плавно возвращается на свой первоначальный уровень. Следовательно, выпуск на одного работника сначала увеличивается по сравнению с начальной траекторией, а затем стабилизируется на более высокой траектории, которая параллельна первоначальной[14]. . Так как
. Так как  - потребление на единицу эффективного труда на траектории сбалансированного роста. Очевидно,
- потребление на единицу эффективного труда на траектории сбалансированного роста. Очевидно,  , за вычетом инвестиций на единицу эффективного труда,
, за вычетом инвестиций на единицу эффективного труда,  . На траектории сбалансированного роста фактические инвестиции равняются восстанавливающим,
. На траектории сбалансированного роста фактические инвестиции равняются восстанавливающим,  . Следовательно,
. Следовательно, (1.19)
(1.19)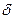 ; значит, мы можем записать
; значит, мы можем записать  . Тогда из выражения (1.19) получаем:
. Тогда из выражения (1.19) получаем: (1.20)
(1.20) , увеличение нормы сбережений может приводить как к увеличению, так и к уменьшению потребления в долгосрочной перспективе. Если
, увеличение нормы сбережений может приводить как к увеличению, так и к уменьшению потребления в долгосрочной перспективе. Если  , умноженную на изменение
, умноженную на изменение  превышает
превышает 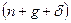 , поэтому увеличение нормы сбережений приводит к сокращению потребления даже когда экономика достигает новой траектории сбалансированного роста. На среднем графике наблюдается обратная картина, и увеличение
, поэтому увеличение нормы сбережений приводит к сокращению потребления даже когда экономика достигает новой траектории сбалансированного роста. На среднем графике наблюдается обратная картина, и увеличение  : линии
: линии 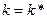 . В этом случае предельное изменение
. В этом случае предельное изменение  . Наша задача - определить, насколько быстро
. Наша задача - определить, насколько быстро  (см. (1.18)). Поэтому можно считать, что
(см. (1.18)). Поэтому можно считать, что  . Если
. Если  в окрестности точки
в окрестности точки  (1.28)
(1.28) величину
величину  . Тогда (1.28) принимает следующий вид:
. Тогда (1.28) принимает следующий вид: (1.29)
(1.29) отрицательно. Следовательно,
отрицательно. Следовательно,  примерно постоянен и равен
примерно постоянен и равен  . Отсюда вытекает, что
. Отсюда вытекает, что (1.30)
(1.30) – начальное значение
– начальное значение  (1.31)
(1.31) , выразив из него
, выразив из него  . Следовательно,
. Следовательно,  . Кроме того, можно показать, что
. Кроме того, можно показать, что  с тем же темпом, что
с тем же темпом, что  .
.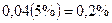 выше своей старой траектории через 1 год, на
выше своей старой траектории через 1 год, на  - через 18 лет и асимптотически стремится к траектории, расположенной выше старой на 5%. Таким образом, даже влияние значительного изменения нормы сбережений сравнительно невелико и реализуется не слишком быстро.[18]
- через 18 лет и асимптотически стремится к траектории, расположенной выше старой на 5%. Таким образом, даже влияние значительного изменения нормы сбережений сравнительно невелико и реализуется не слишком быстро.[18] и различия в эффективности труда
и различия в эффективности труда  раз разницей в капиталовооруженности между рассматриваемыми странами. Если душевые выпуски различаются в
раз разницей в капиталовооруженности между рассматриваемыми странами. Если душевые выпуски различаются в 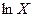 . Так как эластичность душевого выпуска по капиталовооруженности равна
. Так как эластичность душевого выпуска по капиталовооруженности равна  , разность между логарифмами капиталовооруженности должна составлять
, разность между логарифмами капиталовооруженности должна составлять  . Следовательно, капиталовооруженности различаются в
. Следовательно, капиталовооруженности различаются в  , или в
, или в  раз*.
раз*.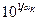 раз. Принимая
раз. Принимая  , получаем отношение капиталовооруженностей, равное
, получаем отношение капиталовооруженностей, равное  . Даже если капитал получает половину дохода, что значительно выше эмпирических наблюдений, капиталовооруженности должны различаться в
. Даже если капитал получает половину дохода, что значительно выше эмпирических наблюдений, капиталовооруженности должны различаться в  раз.
раз. . Эластичность выпуска по капиталу в этом случае равна
. Эластичность выпуска по капиталу в этом случае равна  . Предельная отдача от капитала находится следующим образом:
. Предельная отдача от капитала находится следующим образом: (1.32)
(1.32) . Если
. Если  , то десятикратное различие в выпуске на одного работника, вытекающее из различий в капиталовооруженностях, подразумевает стократное различие в предельных отдачах от капитала. Так как ставка процента равна
, то десятикратное различие в выпуске на одного работника, вытекающее из различий в капиталовооруженностях, подразумевает стократное различие в предельных отдачах от капитала. Так как ставка процента равна  , то различия в ставках процента должны быть ещё больше.
, то различия в ставках процента должны быть ещё больше.


