
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предположения относительно производственной функцииСодержание книги
Поиск на нашем сайте
Важнейшей гипотезой, касающейся производственной функции, является предположение о постоянстве отдачи от масштаба по двум аргументам: капиталу и эффективному труду. Оно, в частности, означает, что удвоение капитала и эффективного труда (например, удвоение Более формально, увеличение объема использованных ресурсов в
Предположение о постоянной отдаче от масштаба можно интерпретировать как комбинацию двух гипотез. Во-первых, экономика предполагается достаточно большой, так что все возможности для специализации уже использованы. В очень маленькой экономике, вероятно, существует достаточно возможностей для специализации, и удвоение капитала и труда увеличивает выпуск более чем в два раза. Однако модель Солоу предполагает, что экономика достаточно большая, и при удвоении труда и капитала, новые факторы производства используются тем же способом, что и уже существующие, поэтому выпуск удваивается. Во-вторых, роль других факторов производства, нежели капитал, труд и знания, сравнительно низка. В частности, мы пренебрегаем землей и другими природными ресурсами. Если природные ресурсы важны, удвоение труда и капитала приведет к увеличению выпуска менее чем в два раза. В разделе 1.8 мы покажем, что ограниченность природных ресурсов, похоже, не является главным ограничением для роста. Следовательно, предположение о постоянной отдаче от масштаба по труду и капиталу является оправданным упрощением действительности. Предположение постоянства отдачи от масштаба позволяет перейти к производственной функции в интенсивной форме. Полагая, что в выражении (1.2)
Отношение
Таким образом, мы можем записать выпуск на единицу эффективного труда как функцию от капиталовооруженности эффективного труда. Новые переменные
Чтобы интуитивно понять смысл выражения (1.4), представим себе экономику, разделенную на AL маленьких частей, с одной единицей эффективного труда и Предполагается, что интенсивная форма производственной функции
Рисунок 1.1 Пример производственной функции
В качестве примера производственной функции часто используется функция Кобба-Дугласа,
Эту производственную функцию легко анализировать. Кроме того, она оказывается хорошим первым приближением для реальных производственных функций. Поэтому она очень полезна. Легко проверить, что функция Кобба-Дугласа обладает постоянной отдачей от масштаба. Умножая факторы производства на
Для того, чтобы получить производственную функцию в интенсивной форме, разделим оба фактора производства на
Из уравнения (1.7) следует, что
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.108.80 (0.007 с.) |

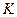 и
и 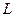 для заданного значения
для заданного значения 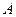 ) удваивает объем произведенных благ.
) удваивает объем произведенных благ. раз увеличивает выпуск во столько же раз:
раз увеличивает выпуск во столько же раз: для любого
для любого  (1.2)
(1.2) , имеем
, имеем . (1.3)
. (1.3) - это капиталовооруженность эффективного труда, а отношение
- это капиталовооруженность эффективного труда, а отношение  , равное
, равное 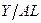 , указывает выпуск на единицу эффективного труда. Обозначим
, указывает выпуск на единицу эффективного труда. Обозначим 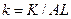 ,
,  , и
, и  . Тогда выражение (1.3) можно переписать в следующем виде:
. Тогда выражение (1.3) можно переписать в следующем виде: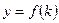 . (1.4)
. (1.4) и
и  не слишком интересны сами по себе. Они скорее составляют инструмент для анализа тех переменных, которые нас в действительности интересуют. Как мы увидим, самый простой способ анализа модели – это сконцентрироваться на динамике
не слишком интересны сами по себе. Они скорее составляют инструмент для анализа тех переменных, которые нас в действительности интересуют. Как мы увидим, самый простой способ анализа модели – это сконцентрироваться на динамике 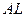 . Мы можем, например, найти выпуск на одного работника,
. Мы можем, например, найти выпуск на одного работника,  , переписав его как
, переписав его как  , или
, или  , и определив динамику
, и определив динамику 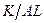 единиц капитала в каждой части. Так как производственная функция обладает постоянной отдачей от масштаба, каждая часть экономики производит долю
единиц капитала в каждой части. Так как производственная функция обладает постоянной отдачей от масштаба, каждая часть экономики производит долю  от выпуска всей экономики. Следовательно, выпуск на единицу эффективного труда зависит только от капиталовооруженности эффективного труда, и не зависит от размеров экономики в целом. Как раз эта идея и выражена в математической форме в выражении (1.4).
от выпуска всей экономики. Следовательно, выпуск на единицу эффективного труда зависит только от капиталовооруженности эффективного труда, и не зависит от размеров экономики в целом. Как раз эта идея и выражена в математической форме в выражении (1.4).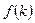 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:  ,
,  ,
,  [6]. Поскольку
[6]. Поскольку  равно
равно  , то предельный продукт капитала
, то предельный продукт капитала  равен
равен  , а это совпадает с
, а это совпадает с 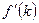 . Следовательно, предположение о том, что функция
. Следовательно, предположение о том, что функция  отрицательной, означает, что предельный продукт капитала положителен и убывает с ростом капиталовооруженности эффективного труда. Также предполагается, что функция
отрицательной, означает, что предельный продукт капитала положителен и убывает с ростом капиталовооруженности эффективного труда. Также предполагается, что функция  ,
,  . Эти условия (более строгие, чем те, что требуются для получения основных результатов модели) означают, что предельный продукт капитала очень высок, если капиталовооруженность достаточно мала, и очень низок, если капиталовооруженность достаточно большая. Эти условия гарантируют, что экономические траектории не расходятся*. Пример производственной функции, удовлетворяющей неравенствам
. Эти условия (более строгие, чем те, что требуются для получения основных результатов модели) означают, что предельный продукт капитала очень высок, если капиталовооруженность достаточно мала, и очень низок, если капиталовооруженность достаточно большая. Эти условия гарантируют, что экономические траектории не расходятся*. Пример производственной функции, удовлетворяющей неравенствам  ,
,  и условиям Инады, представлен на рисунке 1.1.
и условиям Инады, представлен на рисунке 1.1. ,
,  . (1.5)
. (1.5) (1.6)
(1.6) (1.7)
(1.7) . Непосредственно проверяется, что эта функция положительна, стремится к нулю, если
. Непосредственно проверяется, что эта функция положительна, стремится к нулю, если  отрицательна[7].
отрицательна[7].


