
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типы и структуры данных. Опредления, классифиация.Содержание книги
Поиск на нашем сайте
ТИПЫ И СТРУКТУРЫ ДАННЫХ. ОПРЕДЛЕНИЯ, КЛАССИФИАЦИЯ. Тип данных — фундаментальное понятие теории программирования. Тип данных определяет множество значений, набор операций, которые можно применять к таким значениям и, возможно, способ реализации хранения значений и выполнения операций. Любые данные, которыми оперируют программы, относятся к определённым типам. Структура данных — программная единица, позволяющая хранить и обрабатывать множество однотипных и/или логически связанных данных. Структура данных поддерживает определенный порядок доступа к ним. Структуру данных можно рассматривать как своего рода склад или библиотеку. Основные принципы концепции типа: 1) Любой тип данных определяет множество значений, к которым может относиться некоторая константа, которое может принимать переменная, или выражение и которое может формироваться операцией или функцией; 2) Тип любой величины, обозначаемой константой, переменной или выражением, может быть введен по ее виду или по ее описанию, для этого нет необходимости проводить какие-либо вычисления; 3) Каждая операция или функция требует аргументов определенного типа и дает результат также фиксированного типа. Если операция допускает аргументы нескольких типов, то тип результата регламентируется вполне определенными правилами языка. Типы данных – простые типы (не содержат внутри себя никаких других типов). 1) Предопределенные (integer, character, boolean, float) – типы, имеющиеся (строенные) на большинстве выч. машин. Все, кроме вещественного, упорядочены. 2) Перечисляемый – новый, простейший тип, определяющийся простым перечислением входящих в него различных значений (enum color {red, blue, green}; 3) Диапазонный – используется, когда переменной присваивается значение некоторого типа, лежащее только внутри определенного интервала значений (type index = 1..10). Структуры данных – составные типы (определяются с помощью простых типов, их значения обычно представляют собой совокупности значений компонент, относящихся к составляющим их типам; если составляющий тип один, то он называется базовым). 1) Статические (массивы, строки, записи (структуры), объединения, множества, последовательности) – память под них выделяется во время компиляции и сохраняется в течение всей работы программы.
2) Динамические - память под величины отводится во время выполнения программы, а в процессе вычислений изменяются не только значения переменных, но и структура. · Нерекурсивные (массивы); · Рекурсивные (линейные списки, стеки, очереди, деревья, графы) – с применением рекурсии для описания и обработки данных. Преимущества от использования типов данных:
1. Некорректное присваивание. Пусть переменная объявлена как имеющая числовой тип. Тогда попытка присвоить ей символьное или какое-либо другое значение в случае статической типизации приведёт к ошибке компиляции и не даст такой программе запуститься. В случае динамической типизации код программы перед выполнением потенциально опасного действия сравнит типы данных переменной и значения и также выдаст ошибку. Всё это позволяет избежать неправильной работы и «падения» программы. 1. Некорректная операция. Позволяет избежать попыток применения выражений вида «Hello world» + 1. Поскольку, как уже говорилось, все переменные в памяти хранятся как наборы битов, то при отсутствии типов подобная операция была выполнима (и могла дать результат вроде «ello worldǼ»). С использованием типов (см. далее «Контроль типов») такие ошибки отсекаются опять же на этапе компиляции. 2. Некорректная передача параметров. Если функция «синус» ожидает, что ей будет передан числовой аргумент, то передача ей в качестве параметра строки «Hello world» может иметь непредсказуемые последствия. При помощи контроля типов такие ошибки также отсекаются на этапе компиляции. · Стандартизация.
ОБЪЕДИНЕНИЯ. ОПЕРАЦИИ, ПРЕДСТАВЛЕНИЕ. СЛОЖНОСТЬ ОПЕРАЦИЙ. В Паскале – нет В Си – Union <имя> { T1 S1; T2 S2; … Tn Sn; } Все элементы начинаются с одно и того же места в памяти (если присваиваем новое значение элементу объединения, то перезаписываем любое предыдущее присваивание). Объединение может хранить значение только для одного элемента в каждый момент времени. Пример: иллюстрирует использование объединения distance. Сначала программа присваивает значение элементу miles и выводит это значение. Затем программа присваивает значение элементу meters. При этом значение элемента miles теряется:
union distance { walk.miles = 5; Характеристики: 1)Размер – максимальный из размеров компонент sizeof (union) = max(sizeof Ti); 2)Мощность – мощность максимального типа #union = #max(Ti). Операции: 1)Индексация по имени; 2)Присваивание А=В через memcpy; 3)Сравнение А==В через memcmp(A, B, sizeof B); Объединения применяют для записей с вариантами (если в анкете, то каждый последующий порос зависит от предыдущего ответа).
ПОСЛЕДОВАТЕЛЬНОСТИ ВКРАТЦЕ Последовательность - бесконечная структура данных с последовательным доступом, все элементы последовательности имеют один и тот же базовый тип. T: sequence of Tbase Операции: 1)Взятие read x=read() – берем текущий элемент данной последовательности; 2)Добавление (ограничение только по объему памяти) write(x) – добавляем х в конец последовательности; 3)Переход в начало rewind (). Обычно представляет собой однородную структуру, подобную массиву. Но существенная разница в том, что у массива число элементов зафиксировано в его определении, а у последовательности – нет. То есть оно может меняться во время выполнения программы. Хотя каждая последовательность в любой момент времени имеет конкретную конечную длину, мы должны считать мощность последовательного типа бесконечной, т.к. нет никаких ограничений на потенциальную длину последовательностей. Прямое следствие переменной длины – невозможность отвести фиксированный объем памяти под переменные-последовательности. Поэтому память выделяется в ходе выполнения программы, в частности, когда последовательность растет. Таким образом, для работы с последовательностями необходима динамическая схема выделения памяти. Основное правило работы с последовательностями: доступ к элементам осуществляется строго в порядке их следования, а порождается последовательность присоединением новых элементов к ее концу. Следствие – невозможность прямого доступа к элементам, за исключением того элемента, который доступен для просмотра в данный момент. Это и является главным отличием последовательностей от массивов.
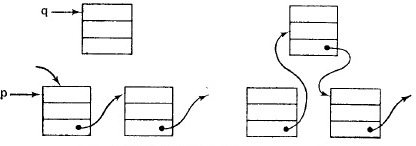
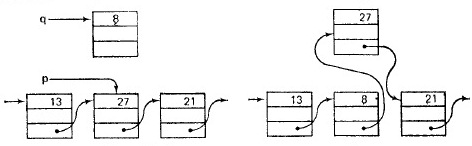
ЛИНЕЙНЫЕ СПИСКИ Линейный список – это множество элементов хранения с заданным отношением строгого порядка, определяющим следование элементов в множестве. Требование строгого порядка вызвано тем, что с каждым элементом линейного списка при хранении связан конкретный физический адрес. Линейный список – либо пустой список, либо элемент, ссылающийся на линейный список. Описание: struct { Tdata data; // поле данных какого-либо произвольного типа struct ls *next; // ls – линейный список, next – указатель на ls (структуру л. с.) } – ссылаемся на структуру, пока ее описание не закончено. Операции: 1)Вставка Имеется указатель на некий элемент p, нужно вставить элемент q: a) после р (через присваивание – не требует сложных операций и памяти)
b) до р (используем случай а, а затем меняем местами
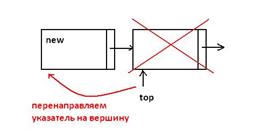
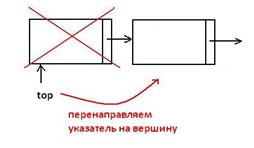
2)Удаление из списка
a) после p: p.next=q.next; free(q); - перенаправляем указатель, освобождаем память. b) до р переписать информацию из p.next в q.next, удалить p.next, используя случай а. Операции удаления/вставки занимают время О(1) и не зависят от длины линейного списка, имеют преимущества по сравнению. Операции поиска и индексации (доступ к элементам) – O(n). Пример применения списка – подсчет количества всех переменных в программе: main() { int i; for (i=0; i<N; i++) {} } Алгоритм: вносим первую встретившуюся переменную в линейный список, увеличиваем ее счетчик, в дальнейшем сверяем каждую прочитанную, есть ли такая в списке, если нет, то добавляем ее в список и увеличиваем ее счетчик, иначе увеличиваем счетчик уже имеющейся в списке переменной, завершаем список.
Двунаправленный линейный список – первый указатель связывает данный элемент со следующим, а второй - с предыдущим. Интересным свойством такого списка является то, что для доступа к его элементам вовсе не обязательно хранить указатель на первый элемент. Достаточно иметь указатель на любой элемент списка. Первый элемент всегда можно найти по цепочке указателей на предыдущие элементы, а последний - по цепочке указателей на следующие. Но наличие указателя на заголовок списка в ряде случаев ускоряет работу со списком. Циклические списки также как и линейные бывают однонаправленными и двунаправленными. Основное отличие циклического списка состоит в том, что в списке нет пустых указателей NULL. Последний элемент списка содержит указатель, связывающий его с первым элементом. Для полного обхода такого списка достаточно иметь указатель только на текущий элемент. В двунаправленном циклическом списке система указателей аналогична системе указателей двунаправленного линейного списка. ОЧЕРЕДИ.
Очередь – рекурсивный безразмерный набор данных, построенный по принципу FIFO. Операции: 1)put(x); - поставить элемент в очередь Занесение элемента в очередь реализуется как добавлению элемента в конец списка. 2)x=get(); - взять элемент из очереди Процедура извлечения элемента из очереди аналогична удалению элемента из начала списка. Реализация очереди: - Первый способ представляет очередь в виде массива и двух целочисленных переменных start и end. Обычно start указывает на голову очереди, end — на элемент, который заполнится, когда в очередь войдёт новый элемент. При добавлении элемента в очередь в q[end] записывается новый элемент очереди, а end уменьшается на единицу. Если значение end становится меньше 1, то мы как бы циклически обходим массив и значение переменной становится равным n. Извлечение элемента из очереди производится аналогично: после извлечения элемента q[start] из очереди переменная start уменьшается на 1. С такими алгоритмами одна ячейка из n всегда будет незанятой (так как очередь с n элементами невозможно отличить от пустой), что компенсируется простотой алгоритмов.
Преимущества данного метода: возможна незначительная экономия памяти по сравнению со вторым способом; проще в разработке. Недостатки: максимальное количество элементов в очереди ограничено размером массива. При его переполнении требуется перевыделение памяти и копирование всех элементов в новый массив. - Линейный список, сложность операции O(1) Второй способ основан на работе с динамической памятью. Очередь представляется в качестве линейного списка, в котором добавление/удаление элементов идет строго с соответствующих его концов. Преимущества данного метода: размер очереди ограничен лишь объёмом памяти. Недостатки: сложнее в разработке; требуется больше памяти; при работе с такой очередью память сильнее фрагментируется; работа с очередью несколько медленнее.
СТЕКИ.
Стек – это линейный список, в котором добавление новых элементов и удаление существующих производится только с одного конца, называемого вершиной стека (упорядоченный набор элементов, в котором размещение новых элементов и удаление осуществляется только с одного конца.). Доступ к элементам организован по принципу LIFO. Операции: 1)push(x) – «втолкнуть» элемент в список Занесение элемента в стек производится аналогично вставке нового элемента в начало списка. Процедура занесения элемента в стек должна содержать два параметра: первый задает вершину стека, в который нужно занести элемент, второй – заносимое значение элемента стека.
2)x=pop(x) – взять элемент из списка В результате выполнения этой операции некоторой переменной i должно быть присвоено значение первого элемента стека, и значение указателя на начало списка должно быть перенесено на следующий элемент стека.
Стеки применяются для вызова процедур (хранение локальных переменных и адреса возврата), рекурсии, обеспечения перебора с возвратом (8 ферзей). Стеки широко применяются в вычислительной технике. Например, для отслеживания точек возврата из подпрограмм используется стек вызовов, который является неотъемлемой частью архитектуры большинства современных процессоров. Языки программирования высокого уровня также используют стек вызовов для передачи параметров при вызове процедур. Пример применения – задача с последовательностью открытых и закрытых скобок (см. конспект). Реализация стека: - линейный список, сложность операций О(1) - Массив
ДЕРЕВЬЯ. ОПРЕДЕЛЕНИЯ, КЛАССИФИКАЦИЯ, СПОСОБЫ ПРЕДСТАВЛЕНИЯ.
Дерево с базовым типом Т – это: 1) Либо пустое дерево 2) Либо вершина типа Т с конечным числом связанных с ней отдельных деревьев с базовым типом Т (поддеревья). (Дерево, на которое ссылается какая-либо вершина – поддерево)
Глубина(высота) = 3
Вершина, на которую непосредственно ссылается другая вершина – ее потомок. Обратная вершина – предок. Вершина, у которой нет потомков – лист дерева. Если пронумеруем вершины так, чтобы каждый следующий потомок был на уровень выше, то вершина, находящаяся на 0 уровне – корень дерева. Вершина, которая не является листом – внутренняя вершина. Уровень какой-либо вершины – глубина (высота), а глубина самого дерева - максимальная глубина из всех ее вершин. Количество непосредственных потомков вершины называется степенью данной вершины, степень дерева – максимальная из всех возможных степеней. Число ветвей (ребер), которые необходимо пройти от корня к вершине х, называется длиной пути к х (корень имеет путь 0). Длина пути всего дерева (длина внутреннего пути) – сумма длин путей до всех его вершин. Средняя длина пути определяется по формуле:
Упорядоченные деревья второй степени называются двоичными деревьями. Деревья n-ной (большей 2) степени называются сильно ветвящимися. Деревья, имеющие минимальную высоту, называются идеально сбалансированными (количество вершин в левом и правом поддереве отличаются не больше чем на 1 – условие для всех вершин).
Выражение таких рекурсивных структур требует использования ссылок. Существует множество различных способов представления деревьев (на примере бинарного дерева): 1) Списочное представление бинарных деревьев основано на элементах, соответствующих узлам дерева. Каждый элемент имеет поле данных и два поля указателей. Один указатель используется для связывания элемента с правым потомком, а другой – с левым. Листья имеют пустые указатели потомков. При таком способе представления дерева обязательно следует сохранять указатель на узел, являющийся корнем дерева. Можно заметить, что такой способ представления имеет сходство с простыми линейными списками. И это сходство не случайно. На самом деле рассмотренный способ представления бинарного дерева является разновидностью мультисписка, образованного комбинацией множества линейных списков. Каждый линейный список объединяет узлы, входящие в путь от корня дерева к одному из листьев.
Tdata data;
struct binary_tree *right; } или struct TREE { Для обработки дерева достаточно знать адрес корневой вершины. Для хранения этого адреса надо ввести ссылочную переменную: Тогда пустое дерево просто определяется установкой переменной Root в нулевое значение:
2) В виде массива проще всего представляется полное бинарное дерево, так как оно всегда имеет строго определенное число вершин на каждом уровне. Вершины можно пронумеровать слева направо последовательно по уровням и использовать эти номера в качестве индексов в одномерном массиве.
Если число уровней дерева в процессе обработки не будет существенно изменяться, то такой способ представления полного бинарного дерева будет значительно более экономичным, чем любая списковая структура. Однако далеко не все бинарные деревья являются полными. Для неполных бинарных деревьев применяют следующий способ представления. Бинарное дерево дополняется до полного дерева, вершины последовательно нумеруются. В массив заносятся только те вершины, которые были в исходном неполном дереве. При таком представлении элемент массива выделяется независимо от того, будет ли он содержать узел исходного дерева. Следовательно, необходимо отметить неиспользуемые элементы массива. Это можно сделать занесением специального значения в соответствующие элементы массива. В результате структура дерева переносится в одномерный массив. Адрес любой вершины в массиве вычисляется как: адрес Главным недостатком рассмотренного способа представления бинарного дерева является то, что структура данных является статической. Размер массива выбирается исходя из максимально возможного количества уровней бинарного дерева. Причем чем менее полным является дерево, тем менее рационально используется память.
ДВОИЧНЫЕ ДЕРЕВЬЯ, ОПЕРАЦИИ.
Двоичное дерево – конечное множество элементов (узлов), которое либо пусто, либо состоит из корня с двумя отдельными двоичными поддеревьями, которые называют левым и правым поддеревом корня. Для построения двоичного дерева с n вершинами, имеющего минимальную высоту, используются следующие правила: 0) Если n=0, то конец; 1) Построить вершину 2) Построить левое поддерево с 3) Построить правое поддерево с Операции с двоичными деревьями: 1) Обход дерева Учитывая рекурсивный характер правил обхода, программная их реализация наиболее просто может быть выполнена с помощью рекурсивных подпрограмм. Каждый рекурсивный вызов отвечает за обработку своего текущего поддерева. После полной обработки текущего поддерева происходит возврат к поддереву более высокого уровня, а для этого надо запоминать и в дальнейшем восстанавливать адрес корневой вершины этого поддерева. Рекурсивные вызовы позволяют выполнить это запоминание и восстановление автоматически, если описать адрес корневой вершины поддерева как формальный параметр рекурсивной подпрограммы.
· Префиксный обход – вершина, левое, правое (+ab):
{ if (t!=0) { print(t->data); //вершина prefix_walk(t->left); // левое prefix_walt(t->right); // правое } } · Инфиксный обход – левое, вершина, правое (a+b); · Постфиксный – левое, правое, вершина (ab+); 2) Поиск: При использовании в целях поиска элементов данных по значению уникального ключа применяются двоичные деревья поиска дерево поиска – все вершины в правом поддереве > x (вершина), все вершины в левом поддереве < x. N элементов можно организовать в бинарное дерево с высотой не более log2(N), поэтому для поиска среди N элементов может потребоваться не больше log2(N) сравнений, если дерево идеально сбалансировано. Отсюда следует, что дерево – это более подходящая структура для организации поиска, чем, например, линейный список.
Ищем 29:
3) Операция включения вершины в дерево: Операция включения элемента в дерево разбивается на три этапа: включение узла в пустое дерево, поиск корня для добавления нового узла, включение узла в левое или правое поддерево. Добавляем 50:
операции поиска, пока не дойдем до NULL.
4) Удаление вершины: Для удаления узла с указанным ключом сначала происходит его поиск. В случае, если узел найден, то он удаляется. · Если удаляемый узел не имеет потомков, то просто удаляется ссылка на него. · Если удаляемый узел имеет одного потомка, в этом случае переадресуется ссылка на этого потомка. · Если удаляемый узел имеет двух потомков, то на его место ставится самый правый потомок из левого поддерева или самый левый потомок из правого поддерева.
Удаляем 15 – ставим 14 или 16
ДЕРЕВО ОПТИМАЛЬНОГО ПОИСКА
Бывают случаи, когда информация о вероятности появления ключа известна. В таких ситуациях характерно постоянство ключей, то есть ключи не добавляются, не удаляются, и сохраняется структура дерева. И для сокращения времени необходимо использование таких деревьев, в которых самые часто встречающиеся вершины находились бы ближе к корню дерева.
1) Будем рассматривать дерево с псевдовершинами. Т. е. обнаружение того факта, что некий ключ k не является ключом в дереве поиска, можно рассматривать,как обращение к псевдовершине (псевдоузлу), вставленной между ближайшими меньшим и большим ключами.
2) Вместо вероятности
(Если поделить 3) Длина средневзвешенного пути:
n – количество вершин, m – количество псевдовершин, ai, bi – вершина и псевдовершина соответственно, hi, hj – уровень вершины, псевдовершины соответственно. Свойство: Любое поддерево дерева оптимального поиска является оптимальным. Т. е. если дерево оптимального поиска разделим пополам относительно вершины, то левои и правое поддерево по основному свойству будут также оптимыльными.
Тогда длина средневзвешенного пути для левого поддерева:
Длина средневзвешенного пути для правого поддерева
W – вес дерева оптимального поиска – количество всех возможных поисков.
Построение дерева: 1) Построение таблицы весов, 2) Достраиваем таблицу, 3) Таблица путей, 4) Сложность
КРАСНО-ЧЕРНЫЕ ДЕРЕВЬЯ.
Свойства: 1) Каждая вершина имеет цвет – красный или черный, 2) Если вершина красная, то оба ее потомка черные, 3) Все пути, ведущие от корня к листьям, содержат одинаковое количество черных вершин.
Красно-черное является подмножеством СДБ, в котором каждый узел может содержать от 1 до 3 значений и, соответственно, от 2 до 4 указателей на потомков. Можно «поднять» красные узлы в графическом представлении красно-черного дерева так, чтобы они оказались на одном уровне по горизонтали со своими предками черными узлами, образуя страницу, тогда будет видно, что горизонтальная ссылка всегда указывает на красную вершину, а вертикальная – на черную.
SPLAY-ДЕРЕВЬЯ. Расширяющееся дерево является двоичным деревом поиска, в котором поддерживается свойство сбалансированности. Это дерево принадлежит классу «саморегулирующихся деревьев», которые поддерживают необходимый баланс ветвления дерева, чтобы обеспечить выполнение операций поиска, добавления и удаления за логарифмическое время от числа хранимых элементов. Это реализуется без использования каких-либо дополнительных полей в узлах дерева (как, например, в Красно-чёрных деревьях или АВЛ-деревьях, где в вершинах хранится, соответственно, цвет вершины и глубина поддерева). Вместо этого «расширяющие операции» (splay operation), частью которых являются вращения, выполняются при каждом обращении к дереву. Учётная стоимость в расчёте на одну операцию с деревом составляет O (logn). Идея: после обращения к вершине мы поднимаем ее к корню. Операции: Splay (расширение) Основная операция дерева. Заключается в перемещении вершины в корень при помощи последовательного выполнения трёх операций: Zig, Zig-Zig и Zig-Zag. Обозначим вершину, которую хотим переместить в корень за x, её родителя - p, а родителя p (если существует) - g. · Zig: выполняется, когда p является корнем.
· Zig-Zig: выполняется, когда и x, и p являются левыми (или правыми) сыновьями. Дерево поворачивается по ребру между g и p, а потом - по ребру между p и x.
· Zig-Zag: выполняется, когда x является правым сыном, а p - левым (или наоборот). Дерево поворачивается по ребру между p и x, а затем - по ребру между x и g.
С одной стороны, Поиск элемента: Если ключ найден, то применяется splay к нему. Иначе применяется к последней вершине, к которой осуществлялся доступ. Добавление элемента: Вставка ->Splay Пример:
Удаление ->Splay к родителю Пример:
Объединение двух деревьев:
t1 t2 Ищем максимальную вершину в t1, проводим с ней splayи ставим ее в корень нового дерева. Split (разделение дерева на две части): Поиск и splayвершины х, по которой будем делить ->Разделяем либо по одному, либо по второму ребру.
АСОЦИАТИВНЫЕ МАССИВЫ И ХЭШИ
Массивы, в которых для обращения к элементам используются ключи, логически связанные со значениями, называют ассоциативными массивами.
Хэш-функции Основным требованиям к хорошей хэш-функции является наиболее равномерное из возможных распределение ключей по диапазону значений индексов. Кроме выполнения этого требования, распределение не связано никакой схемой, и даже желательно, чтобы оно производило впечатление совершенно случайного. Предположим, что имеется функция ord(k), которая определяет порядковый номер ключа k во множестве всех возможных значений ключей. Предположим также, что индексы массива занимают интервал целых чисел 0... N— 1, где N — размер массива. Тогда очевидно, что нужно выбрать следующую функцию: Н (k) = ord(k) mod N.Для нее характерно равномерное распределение ключей на всем интервале индексов, поэтому она служит основой большинства преобразований ключей. Кроме того, она очень эффективно вычисляется при N, равном степени двойки. Но как раз этого случая следует избегать, если ключи являются последовательностями букв: предположение, что все ключи равновероятны, в этом случае совершенно ошибочно, в результате слова, различающиеся лишь несколькими символами, будут с большой вероятностью отображаться в одинаковые индексы, что приведет к чрезвычайно неравномерному распределению. Ситуация, когда в указанном месте нет элемента с заданным ключом, называется конфликтом. Задача формирования альтернативного индекса – решение конфликта.Если обнаруживается, что строка таблицы, соответствующая заданному ключу, не содержит желаемого элемента, то произошел конфликт, т. е. два элемента имеют такие ключи, которые отображаются в один и тот же индекс. В этом случае нужно сформировать еще один индекс. Существует несколько методов формирования вторичного индекса (разрешения конфликтов): 1) Прямое связывание – связывание в линейн
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 517; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.8.97 (0.017 с.) |














 .
.

 Дерево называется упорядоченным, если все ветви, исходящие из любой вершины, также являются упорядоченными.
Дерево называется упорядоченным, если все ветви, исходящие из любой вершины, также являются упорядоченными.
 И - разные!
И - разные!



 struct bynary_tree{
struct bynary_tree{


 struct binary_tree *left;
struct binary_tree *left;

 , где k-номер уровня вершины, i- номер на уровне k в полном бинарном дереве. Адрес корня будет равен единице. Для любой вершины можно вычислить адреса левого и правого потомков: адрес_L
, где k-номер уровня вершины, i- номер на уровне k в полном бинарном дереве. Адрес корня будет равен единице. Для любой вершины можно вычислить адреса левого и правого потомков: адрес_L  и адрес_R
и адрес_R 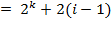
 вершинами;
вершинами; вершинами.
вершинами.


 Каждый рекурсивный вызов прежде всего должен проверить переданный ей адрес на NULL. Если этот адрес равен NULL, то очередное обрабатываемое поддерево является пустым и никакая его обработка не нужна, поэтому просто происходит возврат из рекурсивного вызова. В противном случае в соответствии с реализуемым правилом обхода производится либо обработка вершины, либо рекурсивный вызов для обработки левого или правого поддерева.
Каждый рекурсивный вызов прежде всего должен проверить переданный ей адрес на NULL. Если этот адрес равен NULL, то очередное обрабатываемое поддерево является пустым и никакая его обработка не нужна, поэтому просто происходит возврат из рекурсивного вызова. В противном случае в соответствии с реализуемым правилом обхода производится либо обработка вершины, либо рекурсивный вызов для обработки левого или правого поддерева. prefix_walk (struct binary_tree *t)
prefix_walk (struct binary_tree *t)


 Направляемся в корень, затем в L (<20)
Направляемся в корень, затем в L (<20)
 или R (>20) и т. д.
или R (>20) и т. д.



















 Ищем позицию аналогично
Ищем позицию аналогично




 , будем рассматривать:
, будем рассматривать: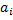 – число поисков вершины
– число поисков вершины  ;
; – число поисков псевдовершины
– число поисков псевдовершины  ,
,  .
. на N, то получится та же самая вероятность)
на N, то получится та же самая вероятность)



 – вес дерева
– вес дерева  (дерево с ключами
(дерево с ключами  ;
; ;
; ;
; .
. .
.



 –сложность доступа, n – количество вершин. В данном случае дерево ведет себя как сбалансированное. С другой стороны, если к каждому элементу осуществлялся хотя бы 1 доступ, то дерево ведет себя как дерево оптимального поиска, т. е. сложность доступа составляет
–сложность доступа, n – количество вершин. В данном случае дерево ведет себя как сбалансированное. С другой стороны, если к каждому элементу осуществлялся хотя бы 1 доступ, то дерево ведет себя как дерево оптимального поиска, т. е. сложность доступа составляет 
 Удаление элемента:
Удаление элемента:




