
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие 2. Прямая и плоскость в пространстве.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
План: 1. Канонические уравнения прямой. 3. Параметрические уравнения прямой. 4. Общее уравнение прямой. 5. Угол между прямыми в пространстве. 6. Расстояние от точки до плоскости. 7. Решение задач. 1. Даны точки M1(-3; 7; -5) и M2(-8; 3; -4). Составить уравнение плоскости, проходящей через точкуM1 и перпендикулярной вектору Ответ: 5x+4y-z-18=0 2. Составить уравнение плоскости, проходящей через три точки M1(1; -3; 4), M2(0; -2; -1), M3(1; 1;-1) Ответ: 15x-5y-4z-14=0 3. Написать уравнение плоскости, проходящей через точки M1(-1; -2; 0) и M2(1; 1; 2) и перпендикулярной плоскости x+2y+2z-4=0 Ответ: 2x-2y+z-2=0 4. Составить уравнение плоскости, проходящей через точку M(-4; 3; -7) параллельно плоскости 6x-5y+4z-15=0 Ответ: 6x-5y+4z+67=0 5. Найти угол между плоскостями и Ответ: π /3 6. Написать уравнение плоскости, параллельной плоскости x-2y+2z-7=0 и отстоящей от нее на расстоянии, равном 5. Ответ: x-2y+2z+8=0 и x-2y+2z-22=0 7. Составить каноничское уравнение прямой, проходящей через точку A(-7; -3; 2) и перпендикулярной плоскости x-4y-5z+8=0. Ответ: (x+7)/2=(y+3)/(-4)=(z+5)/(-5) 8. Написать уравнение прямой l, проходящей через точки A(-1; 2; 3) и B(5; -2; 1) Ответ: (x+1)/6=(y-2)/(-4)=(z-3)/(-2) 9. Общее уравнение прямой Ответ: (x+3)/(-1)=(y-6)/10=z/7 10. Составить параметрические уравнения прямой, проходящей через точку A(-7; -3; 2) и перпендикулярной плоскости x-4y-5z+8=0. Ответ: x=-7+t y=-3-4t z=2-5t 11. Составить уравнение прямой, проходящей через точку M(1; 1; 1) и перпендикулярной векторам Ответ: (x-1)/5=(y-1)/(-1)=(z-1)/(-7) 12. Найти углы, образуемые прямой Занятие 3 Поверхности в пространстве План: 1. Сфера. 2. Поверхности вращения. 3. Цилиндрические и конические поверхности. 4. Приведение общего уравнения поверхности второго порядка к каноническому виду. 5. Решение задач.. Занятие 4. Приведение общего уравнения поверхности второго порядка к каноническому виду. План: 1. Приведение общего уравнения поверхности второго порядка к каноническому виду. Контрольная работа
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ОСВОЕНИЮ УЧЕБНОЙ ДИСЦИПЛИНЫ «ЛИНЕЙНАЯ АЛГЕБРА»
Математическое образование студента специальности «Прикладная информатика (в экономике)» начинается с изучения трех основных дисциплин: математического анализа, аналитической геометрии и высшей алгебры. Эти дисциплины имеют ряд точек соприкосновения и вместе составляют фундамент современной математической науки. Высшая алгебра представляет собой далеко идущее обобщение школьного курса элементарной алгебры. Одна из центральных тем высшей алгебры - изучение произвольных систем уравнений первой степени. Для решения сложных систем разработан аппарат теории определителей, теории матриц. С другой стороны, изучение систем линейных уравнений потребовало введение и изучение векторных и линейных пространств. Линейная алгебра посвященная, в основном, теории матриц и связанной с ней теорией линейных преобразований векторных пространств, включает в себя также теорию форм, теорию инвариантов и тензорную алгебру, играющую важную роль в дифференциальной геометрии (этот раздел алгебры не входит в программу нашего изучения). Истинным объектом алгебраического исследования следует считать алгебраические операции, подобные сложению или умножению чисел, но производимые, возможно, не над числами. Учась в школе, вам приходилось встречаться с операцией сложения сил. Математические дисциплины, изучаемые вами уже на первом курсе, требуют многочисленные алгебраические операции - сложение и умножение матриц, функций, операции над преобразованиями пространства, над векторами и т. д. Эти операции обычно похожи на операции над числами и носят те же названия, но иногда некоторые их свойства оказываются утерянными. Так, очень часто операции оказываются некоммутативными, а иногда неассоциативными. Систематическому изучению подвергаются наиболее важные типы алгебраических систем, для которых определены некоторые алгебраические операции. Таковы, в частности, поля, группы, подгруппы. В последние десятилетия возникла и далеко развилась новая область алгебры – теория структур. Структурой называется алгебраическая система с двумя операциями – сложением и умножением. Эти операции должны быть коммутативны и ассоциативны, а также удовлетворять следующим требованиям: и сумма, и произведение с самим собой должны равняться самому этому элементу. Теория структур имеет тесную связь с теорией групп, с теорией множеств, с геометрией. Мы будем изучать аналитическую геометрию – раздел геометрии, в котором свойства геометрических объектов изучаются методами алгебры. Поясним эти слова. Геометрия, как и другие разделы математики, строится так: сначала формулируются исходные положения – аксиомы, а затем из них выводятся логические следствия – теоремы. Эта часть геометрии называется элементарной, ее вы изучали в школе. Следующий этап в построении геометрии состоит в расширении аппарата путем привлечения средств других разделов математики, в первую очередь алгебры и математического анализа. Делается это так: вводится система координат, в результате чего каждая точка описывается набором чисел, а геометрическая фигура – уравнением и неравенством. Благодаря этому изучение геометрических объектов может быть в ряде случаев сведено к изучению уравнений. Изучение же свойств уравнений осуществляется методами алгебры и математического анализа. Так появились новые разделы геометрии – аналитическая и дифференциальная. Высшая алгебра и аналитическая геометрия требуют глубокого понимания основных понятий, знания определений, теорем, уравнений, описывающих ту или иную геометрическую фигуру, поэтому важно уметь работать с математическим текстом. При работе с математическим текстом придерживайтесь следующих рекомендаций:
· Прочитайте текст не менее двух раз с карандашом в руках, делая выписки основных моментов. · Попробуйте воспроизвести текст, закрыв книгу. · Просмотрите текст еще раз. · Воспроизведите материал, делая вывод формул, доказательства теорем самостоятельно. Балльно-рейтинговая схема предполагает, что студент для получения экзаменационной оценки по данной дисциплине должен набрать до 100 баллов, независимо от формы итогового контроля. Максимум 100 баллов студент может набрать в ходе семестра на аудиторных занятиях, промежуточном контроле и за решения контрольных работ и типовых расчетов. Баллы присуждаются по результатам работы на семинарских занятиях, за посещение в ходе семестра лекций. Максимальное количество баллов за работу на семинаре, можно получить, демонстрируя хорошее знание теоретического материала и умение применять их при решении практических задач. Ответ на экзамене дает студенту от 0 до 40 баллов. Студент, набравший менее 60 баллов, получает итоговую оценку – неудовлетворительно, от 61 до 75 – удовлетворительно, от 76 до 90 - хорошо, 91 и выше баллов - отлично.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.18 (0.009 с.) |

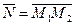
 и
и 
 . Привести ее к каноническому виду.
. Привести ее к каноническому виду. и
и  .
. с осями координат.
с осями координат.


