Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие3. Системы линейных уравнений.Содержание книги
Поиск на нашем сайте
План: 1.Ранг матрицы. Элементарные преобразования матриц. 2.Система линейных уравнений. Решение системы. Равносильность ситемы. 3. Теорема Кронекера – Капели. 4. Матричный метод решения системы. 5. Метод Крамера. 6. Решение задач. 1. 2. 3. 4. Занятие 4. Системы линейных уравнений. План: 1. Метод Гаусса. 2. Исследование системы линейных уравнений. 3. Система линейных однородных уравнений. 4. Решение задач. Решить системы.
Контрольная работа, коллоквиум. ДЕ 2. Занятие 1. Векторы. План: 1.Вектор. Коллинеарность векторов. 2. Равенство векторов. 3. Линейные операции над векторами. 4. Координаты вектора. 5. Проекция вектора на ось. 6. Модуль вектора. 7. Решение задач. 1. В параллелограмме ABCD даны стороны Выразить через
2.В Треугольнике ABC проведены меридианы AK, BL и CM. Выразить
3.На прямой проходящей через точки А (-3;8;2) и B (1;-2;0) найти точку С, абсцисса которой
4.Найти направляющие косинусы вектора
5. Даны векторы
Занятие 2.Скалярное произведение векторов. Векторное произведение векторов. План: 1. Скалярное произведение векторов (определение), свойства. 2. Скалярное произведение в координатной форме. 3. Угол между векторами. 4. Условие перпендикулярности векторов. 5.Определение векторного произведения. 6. Геометрический смысл векторного произведения. 7. Решение задач. 1 Дано 2.Найти угол 3. Даны векторы 4. Даны векторы 5.Даны три последовательные вершины параллелограмма А(-3;-2;0), В(3;-3;1) и С(5;0;2). Найти четвёртую вершину D и угол между векторами 6. Даны векторы 7. Даны векторы 8 Найти площадь треугольника с вершинами А(2;2;2), В(1;3;3), С(3;4;2). 9 Упростить:
10Вычислить площадь треугольника с вершинами А(-3;-2;-4), В(-1;-4;-7), С(1;-2;2). 11. Вычислить площадь и высоту параллелограмма, построенного на векторах 12 Найти площадь параллелограмма, построенного на векторах
13 Вычислить диагонали и площадь параллелограмма, построенного на векторах
Занятие 3. Смешанное произведение векторов. Квадратичные формы. План: 1. Смешанное произведение векторов (определение) и его свойства. 2. Компланарность векторов. 3.Объем параллелепипеда. 4. Деление отрезка в данном отношении. 5. Тестирование. Примерные задания для тестирования. 1. Проверить, является ли векторы Да. Нет. 2. Найти объём тетраэдра с вершинами в точках А(-1;1;0), В(2;-2;1), С(3;1;-1), D(1;0;-2). 6/25 25/6 3/5 3. Вычислить объём параллелепипеда, построенного на векторах 10 куб. ед. 11 куб. ед. 12 куб. ед. 13 куб. ед. 4. Установить, лежат ли в одной плоскости точки А(4;3;10), В(5;1;5), С(2;2;5), D(3;4;12). Да. Нет. 5. В тетраэдре с вершинами D(-3;-3;-3), A(2;-1;-3), B(-1;2;3) и C(-2;-2;1). Найти площадь грани АВС и длину высоты, проведённой к этой грани.
6.Выяснить, компланарны ли векторы Нет. Да. 7. Даны векторы -11/14 -14/11 14/11 11/14 8. Даны векторы
ДЕ 3. Занятие 1. Прямая на плоскости План: 1. Уравнение линии на плоскости. 2. Уравнение прямой с угловым коэффициентом. 3. Уравнение прямой в отрезках. 4. Уравнение прямой, проходящей через две точки. 5. Нормальное уравнение прямой. 6. Общее уравнение прямой. 7. Решение задач. 1. Проверить, принадлежат ли точки A(3; 14), B(4; 13) прямой 7x-3y+21=0 2. Составить уравнение прямой, пересекающей ось Ox в точке (3; 0), а ось оринат в точке (0; 5). Ответ: x/3+y/5=1 3. Вычислить угол наклона прямой Ответ: 120° 4. Составить уравнение прямой, проходящей через начало координат и образующей с осью Ox угол 120° Ответ: 5. Составить уравнение прямой, проходящей через точку (3; 4) и отсекающей на оси Oy отрезок B=2 Ответ: 6. Составить уравнение прямой, проходящей через точку (-3; -2) и образующей с осью Ox угол arctg2. Ответ: 2x-y+4=0 7. Составить уравнение прямой, проходящей через точки A(2; -3), B(-1; 4) Ответ: 7x+3y-5=0 8. Прямая, проходящая через точку A(-2; 3), образует с осью Ox угол 135°. Составить уравение этой прямой. Ответ: x+y-1=0 9. Через точку A(1; 2) проведена прямая, отсекающая на положительных полусях равные отрезки. Составить ее уравнение.
Ответ: x+y-3=0 10. Уравнение прямой привести к нормальному виду. 5x-12y+26=0 Ответ:
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.180.88 (0.009 с.) |






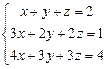







 и
и  векторы
векторы 
 и
и  через векторы
через векторы  и
и  .
. .Выберите правильный ответ.
.Выберите правильный ответ.

 и
и  . Найти векторы:
. Найти векторы:  ;
; 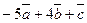 .
. =5,
=5,  =6. Найти скалярное произведение векторов
=6. Найти скалярное произведение векторов  и
и  , если угол
, если угол  между ними равен 120°
между ними равен 120° в треугольнике с вершинами A(1;2;-1), B(5;5;11), C(13;18;20)
в треугольнике с вершинами A(1;2;-1), B(5;5;11), C(13;18;20)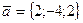 ,
,  ,
,  . Найти проекцию вектора
. Найти проекцию вектора  на вектор
на вектор  .
. и
и  . При каком значении m эти векторы перпендикулярны?
. При каком значении m эти векторы перпендикулярны? и
и  .
. ,
,  и
и  . Найти проекцию вектора
. Найти проекцию вектора  .
. и
и  . При каком значении m векторы перпендикулярны?
. При каком значении m векторы перпендикулярны?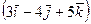


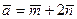 и
и  , где
, где  .
.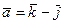 и
и  .
. компланарными?
компланарными? и
и  .
. куб. ед.
куб. ед. куб. ед.
куб. ед. куб. ед.
куб. ед.



 ?
? к оси Ox
к оси Ox