
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения линий на плоскостиСодержание книги Поиск на нашем сайте
Прямая на плоскости Прямую на плоскости можно задать многими способами. При решении задач на прямую часто используются следующие типовые уравнения и соотношения: 1. Уравнения прямой с угловым коэффициентом
где k – угловой коэффициент ( 2. Уравнение прямой, проходящей через данную точку М (x 0, y 0) c данным угловым коэффициентом k
3. Уравнение прямой, проходящей через две данные точки M 1(x 1, y 1) и M 2(x 2, y 2)
Заметим, что в случае 4. Расстояние d от точки М 0 до прямой
5. Угол j, отсчитываемый против часовой стрелки от прямой
Из формулы следует: 1) прямые l 1 и l 2 параллельны, если 2) прямые l 1 и l 2 перпендикулярны, если 6. Уравнения биссектрис углов между прямыми
7. Точка пересечения медиан делит любую из них на части в отношении 2:1 (считая от вершины).
Пример. Даны вершины треугольника А (-3,-3), В(2,7) и С (5,1). Требуется написать уравнения сторон треугольника, определить угол А треугольника, найти уравнение медианы АК и высоты АМ.
Рис. 1. Решение. Чтобы написать уравнение стороны АВ треугольника, используем вид уравнения прямой, проходящей через две точки:
AВ: Аналогично АС: СВ: Тогда тангенс угла А определяется по формуле:
Ищем уравнение медианы АК. Для этого определяем координаты точки К, учитывая, что отрезок ВС в точке К делится пополам и, следовательно,
АК Ищем уравнение высоты АМ, опущенного из вершины А на сторону ВС:
Следовательно, уравнение АМ:
Линии второго порядка Ниже приведены канонические уравнения кривых второго порядка с центром симметрии (в случае параболы – вершиной) в начале координат (случай А) и в точке С (x 0, y 0) (случай В). А В
Пример 1. Пусть задано уравнение х2 + y2 - 4x = 0. Является ли это уравнение уравнением окружности и, если да, то каков ее радиус и координаты центра? Приведем данное уравнение к виду
x2 + y2 - 4x = (x2 - 4x + 4) + y2 - 4 = 0 или (x - 2)2 + y2 = 22. х0 = 2, у0 = 0, R = 2.
Пример 2. Дано уравнение кривой второго порядка Решение. Сравнивая с табличными данными находим, что это парабола, вершига которой находится в точке С (x 0, y 0). приводим уравнение параболы к виду х0 = 0, у0 = 2, р = 1. Чертеж
Рис. 2.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.195.176 (0.009 с.) |

 ,
, ,
,  - угол наклона прямой к оси Ox), b – величина отрезка, отсекаемого прямой на оси Oy.
- угол наклона прямой к оси Ox), b – величина отрезка, отсекаемого прямой на оси Oy. .
. .
. , уравнение принимает вид
, уравнение принимает вид  . Аналогично, если
. Аналогично, если  , уравнение прямой записывается
, уравнение прямой записывается  .
. определяется по формуле
определяется по формуле .
.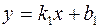 до прямой
до прямой  , определяется по формуле
, определяется по формуле .
.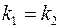 ;
; .
. и
и  имеют вид
имеют вид .
.

 или у = 2х + 3.
или у = 2х + 3. или у = 0,5х -1,5
или у = 0,5х -1,5 или у = -2х +11.
или у = -2х +11. , k2=2, k1 = 0,5. Следовательно
, k2=2, k1 = 0,5. Следовательно 
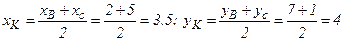
 или
или 
 , где
, где  .
. или у - 0,5х +1,5 =0
или у - 0,5х +1,5 =0









 . Определить тип кривой, найти ее параметры и сделать чертеж.
. Определить тип кривой, найти ее параметры и сделать чертеж. .
.



