
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел и непрерывность функцииСодержание книги Поиск на нашем сайте
Практически предел функции находят не на основании определения предела функции, а на основании теорем о пределе функции. Теорема. Если при 1. 2. 3. 4. Пример 7. Вычислить Решение. Так как
то по теореме о пределе частного получаем, что Но не всегда можно применять теоремы о пределах без предварительного преобразования функций, стоящих под знаком предела. При этом возможны следующие неопределенные ситуации: Приемом раскрытия неопределенности вида При неопределенности вида Неопределенности же вида Пример 8. Вычислить Решение. Наивысшая степень x вторая, делим числитель и знаменатель на
Пример 9. Вычислить Решение. Имеет место неопределенность вида
Пример 10. Вычислить Решение. Числитель и знаменатель дроби при
Пример 11. Вычислить Решение. Так как Выполним преобразования
Пример 12. Найти точки разрыва функции.
Решение. На интервалах Для того чтобы убедиться, что функция непрерывна в точке, требуется проверить, равны ли между собой односторонние пределы и равны ли они значению функции в этой точке. Рассмотрим точку Вычислим односторонние пределы
Так как односторонние пределы не совпадают, Рассмотрим точку
Рис. 3.
Производная Пример 1. Пользуясь формулами дифференцирования, найти производные следующих функций:
Решение. 1.
2.
Производная сложной функции имеет вид
Следовательно,
4. Функция
Находим производные от
Пример 2. Составить уравнение касательной и нормали к кривой Решение. Уравнение касательной к кривой в точке
Для определения углового коэффициента касательной
Подставляя значения
Уравнение нормали
Пример 3. Точка совершает прямолинейное колебательное движение по закону Решение. Найдем скорость
При
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.119.222 (0.007 с.) |

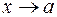 существуют пределы функций
существуют пределы функций 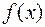 и
и 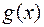 , то:
, то: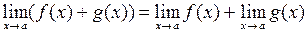 ;
;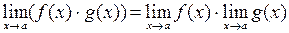 ;
;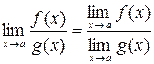 , где
, где 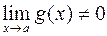 ;
;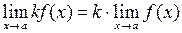 , где
, где  - постоянный множитель.
- постоянный множитель. .
. , а
, а 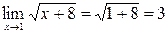 ,
, .
.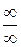 ,
, 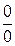 ,
, 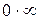 ,
, 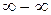 ,
,  .
. требуется выполнить преобразование функции, выделив в числителе и знаменателе дроби множитель, стремящийся к нулю. Затем сократить дробь на этот общий множитель.
требуется выполнить преобразование функции, выделив в числителе и знаменателе дроби множитель, стремящийся к нулю. Затем сократить дробь на этот общий множитель.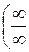 или
или  . Поясним сказанное на примерах.
. Поясним сказанное на примерах.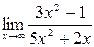 .
.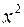 . Получим
. Получим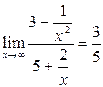 , так как
, так как  и
и  .
.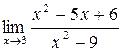 .
.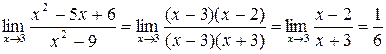 .
.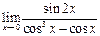 .
.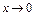 стремятся к нулю. Преобразуем функцию, выделим общий множитель
стремятся к нулю. Преобразуем функцию, выделим общий множитель
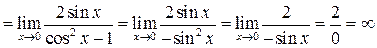 .
. .
. , а
, а 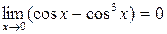 , то имеет место неопределенность вида
, то имеет место неопределенность вида 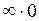 .
.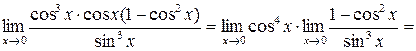
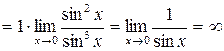 .
.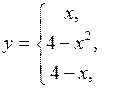 если
если 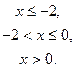
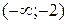 ,
, 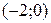 и
и 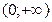 функция непрерывна. Проверке подлежат только точки
функция непрерывна. Проверке подлежат только точки 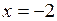 и
и 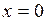 .
.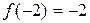 .
.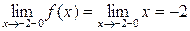 ,
, 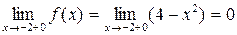 .
.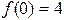 ,
,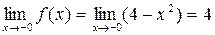 ,
, 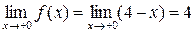 ,
,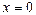 - точка непрерывности функции, выполнены все условия непрерывности.
- точка непрерывности функции, выполнены все условия непрерывности.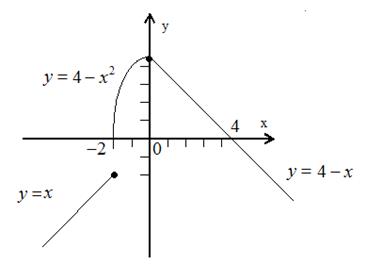
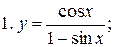
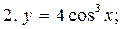
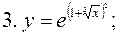 4.
4. 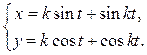
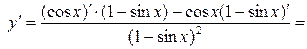
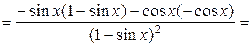
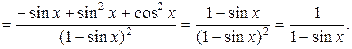
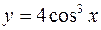 есть сложная функция.
есть сложная функция. , где
, где 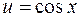 .
.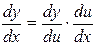 или
или 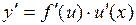 .
.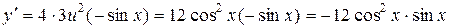 .
. - сложная функция.
- сложная функция. , где
, где 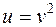 , а
, а 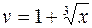 ,
,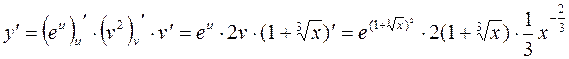 . 4.
. 4. от независимой переменной
от независимой переменной 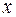 задана через посредство вспомогательной переменной (параметра t). Производная от
задана через посредство вспомогательной переменной (параметра t). Производная от 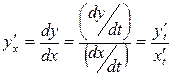 .
.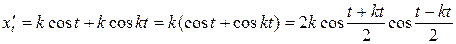 ,
, 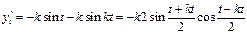 ,
, .
.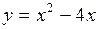 в точке, где
в точке, где 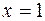 .
.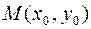
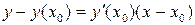 ,
,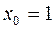 ,
, 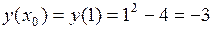 .
. находим производную
находим производную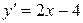 ,
,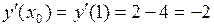 .
.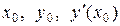 в уравнение, получим
в уравнение, получим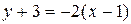 или
или 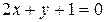 .
.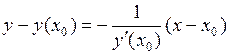 ,
,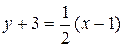 или
или  .
.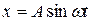 . Определить скорость и ускорение движения в момент времени
. Определить скорость и ускорение движения в момент времени  .
.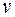 и ускорение а движения в любой момент времени t
и ускорение а движения в любой момент времени t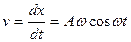 ;
; 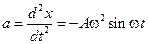 .
.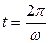
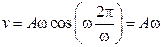 ,
, 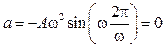 .
.


