
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциал, производные высших порядковСодержание книги Поиск на нашем сайте
Пример 1. Найти дифференциалы функций 1. вычислить Решение. Находим производную данной функции и, умножив ее на дифференциал независимой переменной, получим искомый дифференциал данной функции: 1. 2.
Свойства дифференцируемых функций Пример. Найти пределы используя правило Лопиталя. 1. Решение. Убедившись, что имеет место неопределенность 1.
2.
здесь правило Лопиталя применено дважды. 3.
4.
Исследование поведения функций Пример 1. Исследовать и построить график функции
Решение. 1. Заданная функция определена и непрерывна на всей числовой оси
2. Функция нечетная, ибо 3. График функции пересекается с осями координат только в начале координат, так как 4. Исследуем функцию на наличие асимптот: а) вертикальных асимптот график функции не имеет; б) невертикальная асимптота имеет уравнение
Таким образом, уравнение асимптоты 5. Исследуем функцию на экстремум
Исследуем знак производной на интервале [0; ∞)
Рис. 5.
6. Исследуем график функции на выпуклость и вогнутость
Исследуем знак второй производной на интервале [0; ∞)
Рис. 6
Основываясь на полученных результатах исследования, строим график функции на интервале [0; ∞), затем симметрично полученному графику относительно начала координат на интервале (- ∞; 0)
Рис. 7
Пример 2. Найти наибольшее и наименьшее значения функции
Решение. 1. Найдем критические точки функции 2. Вычислим значения функции на концах отрезка [-4; 4]: 3. Сравнивая все вычисленные значения функции во внутренних критических точках и на концах отрезка, заключаем: наибольшее значение функции
Во многих геометрических, физических и технических задачах требуется найти наибольшее или наименьшее значение величины, связанной функциональной зависимостью с другой величиной. Для решения такой задачи следует, исходя из ее условия, выбрать независимую переменную, а затем найти искомое наибольшее или наименьшее значение полученной функции. При этом интервал изменения независимой переменной, который может быть конечным или бесконечным, также определяется из условия задачи.
Контрольная работа 2. Задания
1. Найти указанные пределы, не пользуясь правилом Лопиталя. При решении примера (в) используйте формулы тригонометрии.
2. Найти точки разрыва функции, если они существуют. Сделать чертеж функции.
3. Найти производные 3.1. а) 3.2. а) в) 3.3. а) в) 3.4. а) в) 3.5. а) в) 3.6. а) в) 3.7. а) в) 3.8. а) в) 3.9. а) в) 3.10.а) в) 3.11.а) в) 3.12.а) в) 3.13.а) в) 3.14.а) в) 3.15.а) в) 3.16.а) в) 3.17.а) в) 3.18.а) в) 3.19.а) в) 3.20.а) в)
3. Найти интервалы монотонности и экстремумы функции.
При выполнении контрольной работы на титульном листе указывается:
фамилия, имя, отчество; номер студенческого билета; название дисциплины, номер контрольной работы, номер варианта.
Номер варианта соответствует последней цифре номера студенческого билета.
Перечень контрольных заданий по методичке кафедры КОНТРОЛЬНАЯ РАБОТА N 1 (методичка к/р 1,2) Нечетный год поступления N 1(1 -10), 2(1 – 10), 3(1 – 10), 4(1 – 10). Четный год поступления N 1(11 -20), 2(11 – 20), 3(11 – 20), 4(11 – 20). КОНТРОЛЬНАЯ РАБОТА N 2 (методичка к/р 1,2) Нечетный год поступления N 1 (1 -10), 2 (1 - 10), 3 (1 - 10), 4 (1 - 10), 5(1 - 10). Четный год поступления N 1 (11 -20), 2 (11 - 20), 3 (11 - 20), 4 (11 - 20), 5(11 - 20).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.195.180 (0.008 с.) |

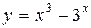 ; 2.
; 2.  ,
, .
. ;
;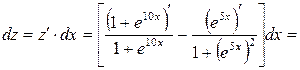
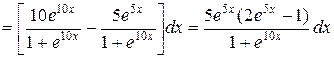 .
. ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  .
. или
или  , применяем затем правило Лопиталя.
, применяем затем правило Лопиталя.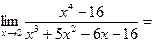

 ;
;


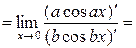
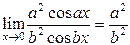 ;
;

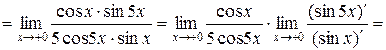
 ;
; .
. .
. .
. , ее график будет симметричен относительно начала координат. Поэтому достаточно построить график для
, ее график будет симметричен относительно начала координат. Поэтому достаточно построить график для  .
. .
. .
.

 ,
,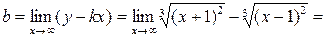

 .
. .
. .
. нигде не обращается в нуль;
нигде не обращается в нуль;  , которые являются критическими.
, которые являются критическими.

 0 1
0 1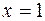 есть точка максимума,
есть точка максимума,  .
. .
. в точке
в точке  ;
;  не существует в точках
не существует в точках  . Эти точки могут быть абциссами точек перегиба.
. Эти точки могут быть абциссами точек перегиба.







 0 1
0 1
 на отрезке [-4; 4].
на отрезке [-4; 4]. , лежащие внутри отрезка [-4; 4], и вычислим ее значения в этих точках:
, лежащие внутри отрезка [-4; 4], и вычислим ее значения в этих точках:  ;
;  в точках
в точках  и
и  . Эти точки лежат внутри отрезка [-4; 4] и являются критическими. Других критических точек нет, так как производная существует всюду. Значение функции в критических точках:
. Эти точки лежат внутри отрезка [-4; 4] и являются критическими. Других критических точек нет, так как производная существует всюду. Значение функции в критических точках:  и
и  .
. и
и  .
. , а ее наименьшее значение равно -41 и достигается на левой границе отрезка
, а ее наименьшее значение равно -41 и достигается на левой границе отрезка  .
.


















































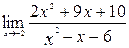





























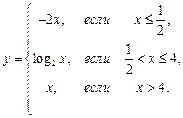
 данных функций.
данных функций. ; б)
; б) 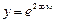 ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
.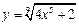 ; б)
; б) 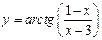 ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. б)
б)  ;
;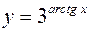 ; г)
; г) 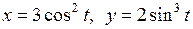 .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б) 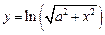 ;
; ; г)
; г) 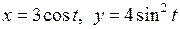 .
. ; б)
; б) 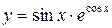 ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
.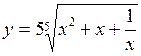 ; б)
; б) 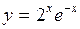 ;
; ; г)
; г)  .
. ; б)
; б)  ;
;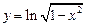 ; г)
; г) 
 ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б) 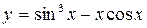 ;
; ; г)
; г)  .
.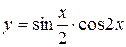 ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
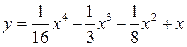 ;
;
 ;
;
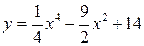 ;
;
 ;
;
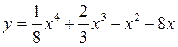 ;
;
 ;
;
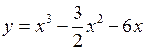 ;
;



