Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. Линии второго порядкаСодержание книги Поиск на нашем сайте
ГЛАВА 3. ЛИНИИ ВТОРОГО ПОРЯДКА Гипербола Определение. Пусть на плоскости заданы две точки F 1и F 2, расстояние между которыми равно 2 c. Пусть, кроме того, задано положительное число a, меньшее c. Гиперболой называется множество точек той же плоскости, для каждой из которых модуль разности расстояний до точек F 1 и F 2, называемых фокусами гиперболы, есть число постоянное, равное 2 а.
Для вывода уравнения гиперболы, которое мы впоследствии назовём каноническим, выберем на плоскости прямоугольную декартову систему координат следующим образом: ось Рис. 3.1.
Чтобы получить уравнение гиперболы остаётся только записать равенство (1) в координатах. В выбранной системе координат фокусы гиперболы имеют следующие координаты: F 1 (– c; 0); F 2 (c; 0). Координаты произвольной (или текущей) точки множества всегда обозначаются x и y. Таким образом, M (x; y). Так как
то уравнение (1) равносильно следующему:
которое, в свою очередь, равносильно уравнению:
Оба эти уравнения являются уравнениями гиперболы, но они имеют громоздкий вид, неудобны для использования и для запоминания, поэтому мы преобразуем их к более простому виду. Проведем следующую цепочку преобразований: (3)
Учитывая, что
Так как
Мы доказали: если точка принадлежит гиперболе, то её координаты удовлетворяют уравнению (3) или (4). Докажем обратное: если координаты точки удовлетворяют уравнению (4) или (3), то она принадлежит гиперболе. Итак, { M (x; y) удовлетворяет (4)}
Аналогично получаем:
Находим разность расстояний:
= Таким образом, (4) – уравнение гиперболы, которое и называется её каноническим уравнением.
Эллипс
Определение. Пусть на плоскости заданы две точки F 1и F 2, расстояние между которыми равно 2 c. Пусть, кроме того, задано число a, большее c. Эллипсом называется множество точек той же плоскости, для каждой из которых сумма расстояний до точек F 1 и F 2, называемых фокусами эллипса, есть число постоянное, равное 2 а.
Вывод канонического уравнения Для вывода канонического уравнения эллипса выберем на плоскости следующую прямоугольную декартову систему координат: ось
то уравнение (1) равносильно следующему:
которое, в свою очередь, равносильно Рис. 3.4 уравнению:
Оба эти уравнения являются уравнениями эллипса, но мы преобразуем их к более простому виду. Проведем следующую цепочку преобразований: (3)
Учитывая, что
Так как
Мы доказали: если точка принадлежит эллипсу, то её координаты удовлетворяют уравнению (3) или (4). Докажем обратное: если координаты точки удовлетворяют уравнению (4) или (3), то она принадлежит эллипсу. Итак, { M (x; y) удовлетворяет (4)}
Аналогично получаем:
Находим сумму расстояний:
Таким образом, (4) – уравнение эллипса, которое и называется его каноническим уравнением.
Парабола
Определение. Пусть на плоскости заданы прямая D и точка F на расстоянии p от неё. Параболой называется множество всех точек той же плоскости, для каждой из которых расстояние до точки F, называемой фокусом параболы, равно расстоянию до прямой D, называемой ее директрисой. Полярные уравнения эллипса, гиперболы и параболы Полярная система координат
Вывод полярных уравнений
Выберем одну из трёх кривых – эллипс, параболу или одну из ветвей гиперболы, и обозначим её
откуда получаем уравнение
Это уравнение задаёт эллипс, параболу, левую ветвь гиперболы, когда полюс находится в левом фокусе, и правую ее ветвь, когда фокус находится в правом фокусе. Если рассматриваемая кривая – эллипс, то Рис.3.15. что
Это означает, что любой луч, выпущенный из фокуса эллипса, пересекает этот эллипс; единственный луч, выпущенный из фокуса параболы и не пересекающий её – это полярная ось; а лучи, выпущенные из фокуса гиперболы и не пересекающие соответствующую её ветвь, образуют целый угол. Упражнение. Покажите, что в той же полярной системе уравнение противоположной ветви гиперболы выглядит так:
Линии второго порядка
Будем считать, что на плоскости задана прямоугольная декартова система координат. Уравнением второй степени с двумя неизвестными называется уравнение вида
в котором Уравнение второй степени называется каноническим, если оно удовлетворяет следующим условиям: 1. не содержит произведения переменных ( 2. если содержит квадрат какой-либо переменной, то не содержит её первой степени ( 3. если содержит первую степень, то только одной переменной, и тогда свободный член равен нулю ( 4. если свободный член не равен нулю, то он равен 1 или -1. Линией второго порядка называется множество точек плоскости, удовлетворяющих какому-либо уравнению 2-й степени. Теорема. Для любой линии второго 2-го порядка на плоскости существует прямоугольная декартова система координат, в которой эта линия задаётся каноническим уравнением. Эту теорему мы докажем позже, в разделе «Линейная алгебра», а сейчас на основании ее мы перечислим все возможные типы линий второго порядка:
ГЛАВА 3. ЛИНИИ ВТОРОГО ПОРЯДКА Гипербола Определение. Пусть на плоскости заданы две точки F 1и F 2, расстояние между которыми равно 2 c. Пусть, кроме того, задано положительное число a, меньшее c. Гиперболой называется множество точек той же плоскости, для каждой из которых модуль разности расстояний до точек F 1 и F 2, называемых фокусами гиперболы, есть число постоянное, равное 2 а.
Для вывода уравнения гиперболы, которое мы впоследствии назовём каноническим, выберем на плоскости прямоугольную декартову систему координат следующим образом: ось Рис. 3.1.
Чтобы получить уравнение гиперболы остаётся только записать равенство (1) в координатах. В выбранной системе координат фокусы гиперболы имеют следующие координаты: F 1 (– c; 0); F 2 (c; 0). Координаты произвольной (или текущей) точки множества всегда обозначаются x и y. Таким образом, M (x; y). Так как
то уравнение (1) равносильно следующему:
которое, в свою очередь, равносильно уравнению:
Оба эти уравнения являются уравнениями гиперболы, но они имеют громоздкий вид, неудобны для использования и для запоминания, поэтому мы преобразуем их к более простому виду. Проведем следующую цепочку преобразований: (3)
Учитывая, что
Так как
Мы доказали: если точка принадлежит гиперболе, то её координаты удовлетворяют уравнению (3) или (4). Докажем обратное: если координаты точки удовлетворяют уравнению (4) или (3), то она принадлежит гиперболе. Итак, { M (x; y) удовлетворяет (4)}
Аналогично получаем:
Находим разность расстояний:
= Таким образом, (4) – уравнение гиперболы, которое и называется её каноническим уравнением.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.18.112.171 (0.008 с.) |

 Вывод канонического уравнения
Вывод канонического уравнения проведем через фокусы гиперболы, а ось
проведем через фокусы гиперболы, а ось  – перпендикулярно ей через середину отрезка F 1 F 2 (рис. 3.1). По определению гиперболе удовлетворяют те, и только те точки М плоскости, для которых
– перпендикулярно ей через середину отрезка F 1 F 2 (рис. 3.1). По определению гиперболе удовлетворяют те, и только те точки М плоскости, для которых . (1)
. (1) ,
,  ,
, , (2)
, (2)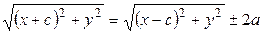 . (3)
. (3)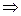



 .
. , разделив последнее уравнение на
, разделив последнее уравнение на  , получаем:
, получаем: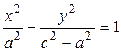 . (4')
. (4') , то
, то  , поэтому найдется такое положительное число
, поэтому найдется такое положительное число  , что
, что  . Теперь уравнение (4') примет вид:
. Теперь уравнение (4') примет вид: . (4)
. (4)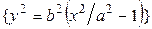

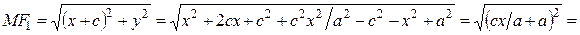
 . (5)
. (5) . (6)
. (6) [(4)
[(4)  ]
] 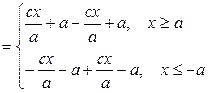 =
=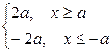 .
. . (1)
. (1) Чтобы получить уравнение эллипса следует записать равенство (1) в координатах. В выбранной системе координат фокусы эллипса имеют следующие координаты: F 1 (– c; 0); F 2 (c; 0). Произвольную (или текущую) точку множества опять обозначаем M (x; y). Так как
Чтобы получить уравнение эллипса следует записать равенство (1) в координатах. В выбранной системе координат фокусы эллипса имеют следующие координаты: F 1 (– c; 0); F 2 (c; 0). Произвольную (или текущую) точку множества опять обозначаем M (x; y). Так как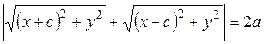 , (2)
, (2)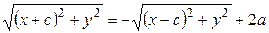 . (3)
. (3)

 .
.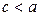 , разделив последнее уравнение на
, разделив последнее уравнение на  , получаем:
, получаем: . (4')
. (4') , то
, то  , поэтому найдется такое положительное число
, поэтому найдется такое положительное число  . Теперь уравнение (4') примет вид:
. Теперь уравнение (4') примет вид: . (4)
. (4)

 . (5)
. (5)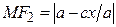 . (6)
. (6) [(4)
[(4)  ]
]  =
=  .
. Выберем на плоскости произвольную точку О, которую назовём полюсом, и проведём луч с началом в этой точке, который назовём полярной осью. Каждой точке
Выберем на плоскости произвольную точку О, которую назовём полюсом, и проведём луч с началом в этой точке, который назовём полярной осью. Каждой точке 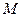 плоскости поставим в соответствие упорядоченную пару чисел
плоскости поставим в соответствие упорядоченную пару чисел  , где
, где  – расстояние от точки
– расстояние от точки 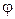 – угол между полярной осью и радиус-вектором точки
– угол между полярной осью и радиус-вектором точки  , а
, а  или
или 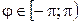 , то это соответствие будет взаимно однозначным на плоскости с выколотой точкой (полюсом).
, то это соответствие будет взаимно однозначным на плоскости с выколотой точкой (полюсом). . Полярную систему координат построим следующим образом: полюс поместим в фокус (для гиперболы берем фокус, соответствующий выбранной ветви), а полярную ось проведём перпендикулярно соответствующей этому фокусу директрисе в направлении от неё. Расстояние от фокуса до директрисыобозначим
. Полярную систему координат построим следующим образом: полюс поместим в фокус (для гиперболы берем фокус, соответствующий выбранной ветви), а полярную ось проведём перпендикулярно соответствующей этому фокусу директрисе в направлении от неё. Расстояние от фокуса до директрисыобозначим  . Число
. Число  называется фокальным параметром кривой. Тогда (рис. 3.15):
называется фокальным параметром кривой. Тогда (рис. 3.15): 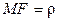 ,
, 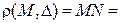
 ;
;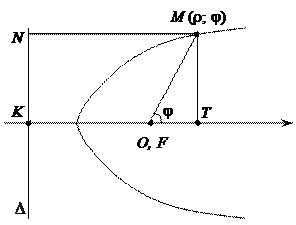
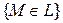
 [Т§ 4]
[Т§ 4] 
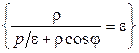
 ,
, (1)
(1) , и из (1) видно,
, и из (1) видно, . Если рассматриваемая кривая – парабола, то
. Если рассматриваемая кривая – парабола, то  и
и  . В случае же, когда рассматривается одна из ветвей гиперболы, причём полюс находится в соответствующем фокусе, то для нахождения
. В случае же, когда рассматривается одна из ветвей гиперболы, причём полюс находится в соответствующем фокусе, то для нахождения  требуется решить неравенство
требуется решить неравенство 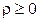 , или
, или  , откуда находим
, откуда находим  . Таким образом, для одной из ветвей гиперболы
. Таким образом, для одной из ветвей гиперболы .
. .
. ,
, .
. при
при  );
); =>
=> 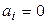 );
); =>
=>  );
);