
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование формы гиперболы по ее каноническому уравнениюСодержание книги
Поиск на нашем сайте
1. Симметрия. Так как координаты x и y в уравнение (4) входят только в чётных степенях, то { M 1(x 0; y 0) Это означает, что гипербола (4) симметрична относительно координатных осей и начала координат. Оси симметрии гиперболы называются осями гиперболы, центр симметрии – ее центром. 2. Пересечение с осями. Если y = 0, то (4) 3. В силу симметрии гиперболы ее достаточно нарисовать в первой координатной четверти, а затем продолжить рисунок по симметрии. Если
Если x = a, то y = 0, если же
Если
 . Рассмотрим ту из них, которая проходит в первой четверти: . Рассмотрим ту из них, которая проходит в первой четверти:
 : :  , значит, гипербола расположена ниже своей асимптоты. Кроме того, ели М – точка гиперболы, Р – точка её асимптоты Рис. 3.2. с такой же первой координатой, , значит, гипербола расположена ниже своей асимптоты. Кроме того, ели М – точка гиперболы, Р – точка её асимптоты Рис. 3.2. с такой же первой координатой,  –расстояние от М до гиперболы (рис.3.2), то –расстояние от М до гиперболы (рис.3.2), то
Теперь можно приступить к рисованию. По обе стороны от начала координат откладываем на действительной оси действительные полуоси, а на мнимой – мнимые. Рисуем прямоугольник, стороны которого проходят через полученные точки параллельно осям координат. Точки пересечения прямоугольника с действительной осью – это вершины гиперболы В заключение параграфа отметим, что уравнение
Эллипс
Определение. Пусть на плоскости заданы две точки F 1и F 2, расстояние между которыми равно 2 c. Пусть, кроме того, задано число a, большее c. Эллипсом называется множество точек той же плоскости, для каждой из которых сумма расстояний до точек F 1 и F 2, называемых фокусами эллипса, есть число постоянное, равное 2 а.
Вывод канонического уравнения Для вывода канонического уравнения эллипса выберем на плоскости следующую прямоугольную декартову систему координат: ось
то уравнение (1) равносильно следующему:
которое, в свою очередь, равносильно Рис. 3.4 уравнению:
Оба эти уравнения являются уравнениями эллипса, но мы преобразуем их к более простому виду. Проведем следующую цепочку преобразований: (3)
Учитывая, что
Так как
Мы доказали: если точка принадлежит эллипсу, то её координаты удовлетворяют уравнению (3) или (4). Докажем обратное: если координаты точки удовлетворяют уравнению (4) или (3), то она принадлежит эллипсу. Итак, { M (x; y) удовлетворяет (4)}
Аналогично получаем:
Находим сумму расстояний:
Таким образом, (4) – уравнение эллипса, которое и называется его каноническим уравнением.
|
||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 610; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.196.5 (0.006 с.) |

 Г}
Г} 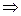 { M 2(– x 0; y 0)
{ M 2(– x 0; y 0)  Г, M 3(– x 0; – y 0)
Г, M 3(– x 0; – y 0)  в точках A 1 (– a; 0) и A 2 = (a; 0), которые называются вершинами гиперболы. Если же x = 0, то (4) решений не имеет, т.е. ось
в точках A 1 (– a; 0) и A 2 = (a; 0), которые называются вершинами гиперболы. Если же x = 0, то (4) решений не имеет, т.е. ось  гипербола не пересекает. Та ось гиперболы, которую она пересекает, называется её действительной осью, а та, которую не пересекает – мнимой. Числа a и b называются полуосями гиперболы, действительной и мнимой соответственно.
гипербола не пересекает. Та ось гиперболы, которую она пересекает, называется её действительной осью, а та, которую не пересекает – мнимой. Числа a и b называются полуосями гиперболы, действительной и мнимой соответственно. ,
, 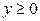 , то из (4) можно выразить y:
, то из (4) можно выразить y: . (7)
. (7) , то и
, то и  . Вычислим производную:
. Вычислим производную: .
. , то
, то  , поэтому гипербола в вершине имеет вертикальную касательную.
, поэтому гипербола в вершине имеет вертикальную касательную.

 . (8)
. (8)

 .
. Следовательно, при неограниченном удалении от начала координат гипербола бесконечно близко приближается к своей асимптоте, не пересекая ее.
Следовательно, при неограниченном удалении от начала координат гипербола бесконечно близко приближается к своей асимптоте, не пересекая ее. и
и  . Затем проводим диагонали прямоугольника и продляем их – это асимптоты гиперболы. Рисуем гиперболу сначала в первой четверти, начиная от вершины и неограниченно приближая её к асимптоте, а затем продолжаем по симметрии в остальные координатные четверти (рис. 3.3).
. Затем проводим диагонали прямоугольника и продляем их – это асимптоты гиперболы. Рисуем гиперболу сначала в первой четверти, начиная от вершины и неограниченно приближая её к асимптоте, а затем продолжаем по симметрии в остальные координатные четверти (рис. 3.3). задаёт гиперболу, действительной осью которой является ось
задаёт гиперболу, действительной осью которой является ось 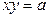 при
при  – это уравнение гиперболы с перпендикулярными асимптотами, составленное относительно её асимптот.
– это уравнение гиперболы с перпендикулярными асимптотами, составленное относительно её асимптот. . (1)
. (1) Чтобы получить уравнение эллипса следует записать равенство (1) в координатах. В выбранной системе координат фокусы эллипса имеют следующие координаты: F 1 (– c; 0); F 2 (c; 0). Произвольную (или текущую) точку множества опять обозначаем M (x; y). Так как
Чтобы получить уравнение эллипса следует записать равенство (1) в координатах. В выбранной системе координат фокусы эллипса имеют следующие координаты: F 1 (– c; 0); F 2 (c; 0). Произвольную (или текущую) точку множества опять обозначаем M (x; y). Так как ,
,  ,
,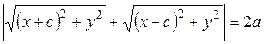 , (2)
, (2)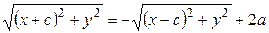 . (3)
. (3)


 .
.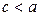 , разделив последнее уравнение на
, разделив последнее уравнение на  , получаем:
, получаем: . (4')
. (4') , то
, то  , поэтому найдется такое положительное число
, поэтому найдется такое положительное число  , что
, что  . Теперь уравнение (4') примет вид:
. Теперь уравнение (4') примет вид: . (4)
. (4)

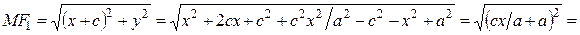
 . (5)
. (5)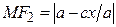 . (6)
. (6) [(4)
[(4)  ]
]  =
=  .
.


