Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Касательные к эллипсу, гиперболе, параболеСодержание книги
Поиск на нашем сайте
Во-первых, вспомним, что уравнение касательной к графику функции
Пусть задано некоторое уравнение
Если Составим уравнение касательной к гиперболе
в принадлежащей ей точке
откуда при
Тогда
Умножив это уравнение на
которое равносильно следующему:
В силу того, что точка
Замечание. Уравнение (4) получено при условии, что Таким же образом составим и уравнение касательной к параболе
в принадлежащей ей точке (5)
Замечание. Если Упражнение. Покажите, что уравнение касательной к эллипсу
в принадлежащей ему точке
Оптические свойства эллипса, гиперболы и параболы
Теорема. Лучи света, выходящий из одного фокуса эллипса, после отражения от эллипса проходят через другой его фокус (рис. 3.16).
► Для гиперболы. Покажем, что нормаль
Для параболы. Обозначим
Сравнивая (5) и (6), опять же получаем, что Для эллипса оптическое свойство до- Рис. 3.18 казывается точно так же, как и для гиперболы, поэтому вы можете сделать это самостоятельно в качестве упражнения. ◄
Линии второго порядка
Будем считать, что на плоскости задана прямоугольная декартова система координат. Уравнением второй степени с двумя неизвестными называется уравнение вида
в котором Уравнение второй степени называется каноническим, если оно удовлетворяет следующим условиям: 1. не содержит произведения переменных ( 2. если содержит квадрат какой-либо переменной, то не содержит её первой степени ( 3. если содержит первую степень, то только одной переменной, и тогда свободный член равен нулю ( 4. если свободный член не равен нулю, то он равен 1 или -1. Линией второго порядка называется множество точек плоскости, удовлетворяющих какому-либо уравнению 2-й степени. Теорема. Для любой линии второго 2-го порядка на плоскости существует прямоугольная декартова система координат, в которой эта линия задаётся каноническим уравнением. Эту теорему мы докажем позже, в разделе «Линейная алгебра», а сейчас на основании ее мы перечислим все возможные типы линий второго порядка:
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 2189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.117.52 (0.006 с.) |

 в точке
в точке  выглядит так:
выглядит так: . (1)
. (1) . (2)
. (2) существует единственное число
существует единственное число  такое, что
такое, что  , то говорят, что уравнение (2) на промежутке
, то говорят, что уравнение (2) на промежутке  задаёт некоторую функцию
задаёт некоторую функцию  зависящей от переменной
зависящей от переменной  .
. . (3)
. (3)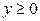 , а вторую при
, а вторую при 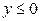 . Для нахождения производной дифференцируем равенство (3):
. Для нахождения производной дифференцируем равенство (3): ,
, находим
находим .
.
 . Используя (1), запишем уравнение касательной к гиперболе (3) в точке
. Используя (1), запишем уравнение касательной к гиперболе (3) в точке 
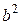 , получим уравнение:
, получим уравнение: ,
, .
. . (4)
. (4) , то
, то  . Тогда из (4) следует, что
. Тогда из (4) следует, что  или
или  , что совпадает с уравнением касательной к гиперболе в её вершине. Таким образом, несмотря на то, что уравнение касательной к гиперболе в некоторой ее точке выводилось при условии, что эта точка не является вершиной, окончательное уравнение (4) подходит и для вершины тоже.
, что совпадает с уравнением касательной к гиперболе в её вершине. Таким образом, несмотря на то, что уравнение касательной к гиперболе в некоторой ее точке выводилось при условии, что эта точка не является вершиной, окончательное уравнение (4) подходит и для вершины тоже. (5)
(5)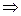



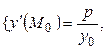




 . (6)
. (6) – это вершина параболы. При условии
– это вершина параболы. При условии  из (6) получаем
из (6) получаем  . Это уравнение оси
. Это уравнение оси  , которая и является касательной к параболе в её вершине. Таким образом, полученное уравнение (6) задаёт касательную к параболе во всех ее точках, несмотря на то, что выводилось оно при условии
, которая и является касательной к параболе в её вершине. Таким образом, полученное уравнение (6) задаёт касательную к параболе во всех ее точках, несмотря на то, что выводилось оно при условии  .
.
 .
. Лучи света, выходящие из одного фокуса гиперболы, после отражения от гиперболы кажутся выходящими из другого её фокуса (рис. 3.18).
Лучи света, выходящие из одного фокуса гиперболы, после отражения от гиперболы кажутся выходящими из другого её фокуса (рис. 3.18). к гиперболе в ее точке
к гиперболе в ее точке  образует одинаковые углы с лучом, выходящим из правого фокуса, и с лучом, кажущимся выходящим из левого фокуса. Обозначим
образует одинаковые углы с лучом, выходящим из правого фокуса, и с лучом, кажущимся выходящим из левого фокуса. Обозначим  (рис. 3.17). Согласно (4) § 6
(рис. 3.17). Согласно (4) § 6  . Так как
. Так как  , то
, то 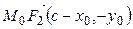 ,
, 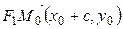 . Тогда:
. Тогда: , (1)
, (1) . (2)
. (2) Сравнивая (1) и (2) и учитывая, что оба угла
Сравнивая (1) и (2) и учитывая, что оба угла  и
и  находятся в пределах от 0 до
находятся в пределах от 0 до  , получаем, что
, получаем, что  ,
,  (рис. 3.18). На основании (6) § 6
(рис. 3.18). На основании (6) § 6  . Тогда
. Тогда  и
и

 , ( 5)
, ( 5) . (6)
. (6) .
. ,
, .
. при
при  );
); =>
=> 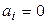 );
); =>
=>  );
);