
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эксцентриситет и директрисы эллипса и гиперболыСодержание книги
Поиск на нашем сайте
Эксцентриситетом гиперболы называется число e, равное отношению половины расстояния между фокусами гиперболы к ее действительной полуоси. Эксцентриситетом эллипса называется число e, равное отношению половины расстояния между фокусами эллипса к его большой полуоси. Директрисами гиперболы называются прямые, перпендикулярные ее действительной оси и находящиеся от центра на расстоянии, равном отношению действительной полуоси к эксцентриситету. Директрисами эллипса называются прямые, перпендикулярные его большой оси и находящиеся от центра на расстоянии, равном отношению большой полуоси к эксцентриситету.
 , т.к. , т.к.  . Вспомнив, что . Вспомнив, что 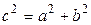 , получаем , получаем 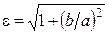 . Исследуем, как меняется форма гиперболы в зависимости от её эксцентриситета. Зафиксируем полуось . Исследуем, как меняется форма гиперболы в зависимости от её эксцентриситета. Зафиксируем полуось  . Если . Если  , то , то 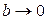 , т.е. гипербола будет очень узкой. С ростом , т.е. гипербола будет очень узкой. С ростом  растёт и растёт и  , т.е. ветви гиперболы расширяются (см. рис. 3.9). Если же , т.е. ветви гиперболы расширяются (см. рис. 3.9). Если же 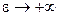 , то и , то и 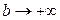 , т.е. гипербола по внешнему виду приближается к паре параллельных прямых. , т.е. гипербола по внешнему виду приближается к паре параллельных прямых.
Рис.3.9 Теперь вернемся к директрисам. Так как для гиперболы (1) то для гиперболы Теорема (основное свойство эллипса и гиперболы по отношению к директрисам). Для всех точек гиперболы (эллипса) отношение расстояния до фокуса к расстоянию до соответствующей этому фокусу директрисы есть число постоянное, равное эксцентриситету гиперболы (эллипса). И обратно: если для какой-либо точки плоскости отношение расстояния до фокуса заданной гиперболы (эллипса) к расстоянию до соответствующей этому фокусу директрисы равно эксцентриситету заданной гиперболы (эллипса), то эта точка принадлежит гиперболе
►Докажем утверждение для левого фокуса и левой директрисы гиперболы (1) (в остальных случаях вы его докажете самостоятельно в качестве упражнения). На рис. 3.13 точки имеют следующие координаты:
Докажем обратное утверждение. Пусть для некоторой точки
Так как (3)
Учитывая, что На основании доказанной теоремы мы можем сформулировать общее определение эллипса, гиперболы и параболы. Определение. Гиперболой (эллипсом, параболой) называется множество точек плоскости, для каждой из которых отношение расстояния до заданной точки к расстоянию до заданной прямой в этой плоскости есть число постоянное, равное e, причём e > 1 (e < 1, e = 1).
Полярные уравнения эллипса, гиперболы и параболы Полярная система координат
Вывод полярных уравнений
Выберем одну из трёх кривых – эллипс, параболу или одну из ветвей гиперболы, и обозначим её
откуда получаем уравнение
Это уравнение задаёт эллипс, параболу, левую ветвь гиперболы, когда полюс находится в левом фокусе, и правую ее ветвь, когда фокус находится в правом фокусе. Если рассматриваемая кривая – эллипс, то Рис.3.15. что
Это означает, что любой луч, выпущенный из фокуса эллипса, пересекает этот эллипс; единственный луч, выпущенный из фокуса параболы и не пересекающий её – это полярная ось; а лучи, выпущенные из фокуса гиперболы и не пересекающие соответствующую её ветвь, образуют целый угол. Упражнение. Покажите, что в той же полярной системе уравнение противоположной ветви гиперболы выглядит так:
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1571; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.203 (0.009 с.) |

 , (1)
, (1)
 , (1I)
, (1I)
 , a > b (2)
, a > b (2)
 ,
,
 ,
,
 .
.
 .
.
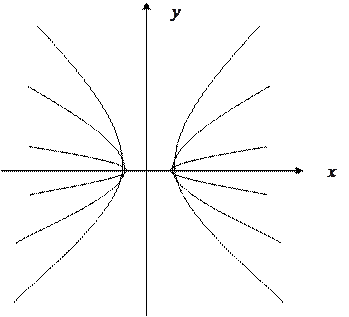
 Рассмотрим теперь эллипс ( 2 ). Для него
Рассмотрим теперь эллипс ( 2 ). Для него  , т.к.
, т.к. 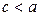 . Для эллипса (2)
. Для эллипса (2) , поэтому
, поэтому  . Исследуем, как меняется форма эллипса в зависимости от его эксцентриситета. Опять зафиксируем полуось
. Исследуем, как меняется форма эллипса в зависимости от его эксцентриситета. Опять зафиксируем полуось  получаем
получаем  , и эллипс вырождается в окружность. С ростом
, и эллипс вырождается в окружность. С ростом  , т.е. эллипс и вовсе стремится превратиться в отрезок (рис 3.10).
, т.е. эллипс и вовсе стремится превратиться в отрезок (рис 3.10). , Рис. 3.10
, Рис. 3.10 , а для эллипса
, а для эллипса 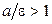 . Это значит, что и директрисы гиперболы, и директрисы эллипса свою кривую не пересекают. Кроме того, директриса и соответствующий ей фокус отделены кривой друг от друга (рис. 3.11 и 3.12).
. Это значит, что и директрисы гиперболы, и директрисы эллипса свою кривую не пересекают. Кроме того, директриса и соответствующий ей фокус отделены кривой друг от друга (рис. 3.11 и 3.12). (эллипсу).
(эллипсу).
 ,
,  ,
,  . Тогда
. Тогда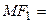 [§1, (5)] =
[§1, (5)] =  ;
; 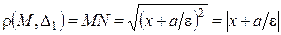 .
. Из этих двух равенств и получаем:
Из этих двух равенств и получаем: .
. плоскости справедливо соотношение:
плоскости справедливо соотношение: . (3)
. (3) , а
, а  , то
, то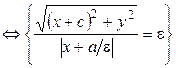

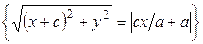

 .
. , из последнего уравнения получаем
, из последнего уравнения получаем 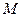 удовлетворяет уравнению заданной гиперболы. ◄
удовлетворяет уравнению заданной гиперболы. ◄ Выберем на плоскости произвольную точку О, которую назовём полюсом, и проведём луч с началом в этой точке, который назовём полярной осью. Каждой точке
Выберем на плоскости произвольную точку О, которую назовём полюсом, и проведём луч с началом в этой точке, который назовём полярной осью. Каждой точке  , где
, где  – расстояние от точки
– расстояние от точки 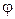 – угол между полярной осью и радиус-вектором точки
– угол между полярной осью и радиус-вектором точки  , а
, а  или
или 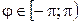 , то это соответствие будет взаимно однозначным на плоскости с выколотой точкой (полюсом).
, то это соответствие будет взаимно однозначным на плоскости с выколотой точкой (полюсом). . Полярную систему координат построим следующим образом: полюс поместим в фокус (для гиперболы берем фокус, соответствующий выбранной ветви), а полярную ось проведём перпендикулярно соответствующей этому фокусу директрисе в направлении от неё. Расстояние от фокуса до директрисыобозначим
. Полярную систему координат построим следующим образом: полюс поместим в фокус (для гиперболы берем фокус, соответствующий выбранной ветви), а полярную ось проведём перпендикулярно соответствующей этому фокусу директрисе в направлении от неё. Расстояние от фокуса до директрисыобозначим  . Число
. Число  называется фокальным параметром кривой. Тогда (рис. 3.15):
называется фокальным параметром кривой. Тогда (рис. 3.15): 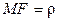 ,
, 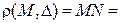
 ;
;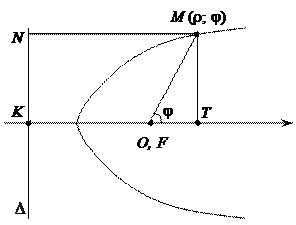
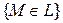

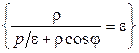
 ,
, (1)
(1) . Если рассматриваемая кривая – парабола, то
. Если рассматриваемая кривая – парабола, то  и
и  . В случае же, когда рассматривается одна из ветвей гиперболы, причём полюс находится в соответствующем фокусе, то для нахождения
. В случае же, когда рассматривается одна из ветвей гиперболы, причём полюс находится в соответствующем фокусе, то для нахождения  требуется решить неравенство
требуется решить неравенство 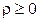 , или
, или  , откуда находим
, откуда находим  . Таким образом, для одной из ветвей гиперболы
. Таким образом, для одной из ветвей гиперболы .
. .
.


