
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения. ЛинеаризацияСодержание книги
Поиск на нашем сайте
Известно, что любое движение, процессы передачи, обмена, преобразования энергии и вещества математически можно описать в виде дифференциальных уравнений (ДУ). Любые процессы в АСР также можно описать дифференциальными уравнениями, которые определяют сущность происходящих в системе процессов независимо от ее конструкции и т.д. Решив ДУ, можно найти характер изменения регулируемой переменной в переходных и установившихся режимах при различных воздействиях на систему. Для упрощения задачи нахождения ДУ, описывающего работу АСР в целом, систему разбивают на ее отдельные элементы, переходные процессы в которых описываются достаточно простыми ДУ. Так как ДУ описывают работу системы независимо от физической сущности протекающих в ней процессов, то при декомпозиции системы нет необходимости учитывать их физическую целостность. Для каждого элемента структурной схемы необходимо составить ДУ, определяющее зависимость изменения выходной величины от входной. Так как выходная величина предыдущего элемента является входной для последующего, то, определив ДУ отдельных элементов, можно найти ДУ системы. Однако такой метод применим только в частных случаях. Дело в том, что в большинстве случаев в реальных элементах системы связь между входной и выходной величинами является нелинейной и часто задается в графической форме. Поэтому, даже если ДУ системы и будет получено, оно будет нелинейным. А аналитическое решение нелинейных ДУ возможно далеко не всегда. Для решения этой проблемы учитывают, что в процессе регулирования отклонения всех изменяющихся величин от их установившихся значений малы, и поэтому возможна замена нелинейных ДУ приближенными линейными ДУ, то есть возможна линеаризация дифференциальных уравнений.
Графически линеаризацию некоторого уравнения от двух переменных F(х,у) = 0 в окрестности некоторой точки (х0, у0) можно представить как замену рассматриваемого участка кривой на касательную (см. рисунок 1.17), уравнение которой определяется по формуле
где Линеаризация ДУ происходит аналогично, отличие состоит только в том, что необходимо искать частные производные по производным ( Пример. Линеаризация нелинейного ДУ. 3xy - 4x2 + 1,5 Данное ДУ является нелинейным из-за наличия произведений переменных х и у. Линеаризируем его в окрестности точки с координатами х0 = 1, 3у0 - 4 + 0 = 0 + у0, откуда у0 = 2. Введем в рассмотрение функцию F = 3xy - 4x2 + 1,5x’y - 5y’ - y и определим все ее производные при заданных начальных условиях:
Теперь, используя полученные коэффициенты, можно записать окончательное линейное ДУ: -5.Dy’ + 2.Dy + 3.Dх’ - 2.Dх = 0. ¨ Линеаризация ДУ, заданного в явном виде относительно у, т.е. y = F(x) производится по формуле
то есть в данном случае нет необходимости искать производные по у.
2.5 Преобразования Лапласа Исследование АСР существенно упрощается при использовании прикладных математических методов операционного исчисления, поскольку позволяет от решения ДУ перейти к решению алгебраических уравнений. Например, функционирование некоторой системы описывается ДУ вида
где х и у - входная и выходная величины. Если в данное уравнение вместо x(t) и y(t) подставить функции X(s) и Y(s) комплексного переменного s такие, что
то исходное ДУ при нулевых начальных условиях равносильно линейному алгебраическому уравнению a2 s2 Y(s) + a1 s Y(s) + a0 Y(s) = b1 X(s) + b0 X(s). Такой переход от ДУ к алгебраическому уравнению называется преобразованием Лапласа, формулы (2.2) соответственно формулами преобразования Лапласа, а полученное уравнение - операторным уравнением. Новые функции X(s) и Y(s) называются изображениями x(t) и y(t) по Лапласу, тогда как x(t) и y(t) являются оригиналами по отношению к X(s) и Y(s). Переход от одной модели к другой достаточно прост и заключается в замене знаков дифференциалов
Таблица 1.1 - Преобразования Лапласа
Таблица 1.2 - Формулы обратного преобразования Лапласа (дополнение)
Для обратного перехода от операторного уравнения к функциям от времени используется метод обратного преобразования Лапласа. Общая формула обратного преобразования Лапласа:
где f(t) - оригинал, F(jw) - изображение при s = jw, j - мнимая единица, w - частота. Эта формула достаточно сложна, поэтому были разработаны специальные таблицы (см. таблицы 1.1 и 1.2), в которые сведены наиболее часто встречающиеся функции F(s) и их оригиналы f(t). Они позволяют отказаться от прямого использования формулы (2.3). Более полные таблицы преобразований Лапласа можно найти, например, в [22, 23]. Существует несколько теорем преобразования Лапласа. Теорема 1. Теорема линейности. Изображение суммы функций равно сумме изображений, то есть, если f1 имеет изображение F1(s) (или более кратко f1 «F1(s)), f2 «F2(s) и т.д., то a1.f1 + a2.f2 + … + an.fn «a1.F1(s) + a2.F2(s) + … + an.Fn(s). Теорема 2. Теорема дифференцирования. Если f(t) имеет изображение F(s), то при нулевых начальных условиях (т.е. при f(0) = 0, f’(0) = 0 и т.д.) производные f(t) будут иметь изображения: f’(t) «s.F(s) – для первой производной, f ”(t) «s2.F(s) – для второй производной, f(n)(t) «sn.F(s) – для n-й производной. При ненулевых начальных условиях: f’(t) «s.F(s) – f(0) – для первой производной, f ”(t) «s2.F(s) – s.f(0) – f’(0) – для второй производной, f(n)(t) «sn.F(s) – sn-1.f(0) - sn-2.f’(0) - … - f(n-1)(0) – для n-й. Теорема 3. Теорема смещения. f(t).ea×t «F(s - a). Например, если 1(t) « Теорема 4. Теорема запаздывания. f(t - t) «F(s).e-t×s, где t - запаздывание по времени. Например, если 1(t) « Теорема 5. Теорема интегрирования.
Теорема 6. О начальных и конечных значениях.
где f(0) – начальное значение функции (при t = 0), fуст – конечное (значение в установившемся режиме). Закон изменения выходного сигнала обычно является функцией, которую необходимо найти, а входной сигнал, как правило, известен. Некоторые типовые входные сигналы были рассмотрены в п. 2.3. Здесь приводятся их изображения: единичное ступенчатое воздействие имеет изображение X(s) = дельта-функция X(s) = 1, линейное воздействие X(s) = Пример. Решение ДУ с использованием преобразований Лапласа.
Допустим, входной сигнал имеет форму единичного ступенчатого воздействия, т.е. x(t) = 1. Тогда изображение входного сигнала, согласно таблице 1.1, имеет вид X(s) = Производим преобразование исходного ДУ по Лапласу и подставляем X(s): s2×Y(s) + 5×s×Y(s) + 6×Y(s) = 2×s×X(s) + 12×X(s), s2×Y(s) + 5×s×Y(s) + 6×Y(s) = 2×s Y(s)×(s3 + 5s2 + 6s) = 2×s + 12. Определяется выражение для Y:
Оригинал полученной функции отсутствует в таблице оригиналов и изображений. Для решения задачи его поиска дробь разбивается на сумму простых дробей с учетом того, что знаменатель может быть представлен в виде s(s + 2)(s + 3):
Теперь, используя табличные функции (см. таблицы 1.1 и 1.2), определяется оригинал выходной функции: y(t) = 2 - 4.e-2t + 2.e-3t. ¨ При решении ДУ с использованием преобразований Лапласа часто встает промежуточная задача разбиения дроби на сумму простых дробей. Существуют два пути решения этой задачи: - путем решения системы уравнений относительно коэффициентов числителей, - путем расчета коэффициентов числителей по известным формулам. Общий алгоритм разбиения дроби на сумму простых дробей: шаг 1 – определяются корни знаменателя si (знаменатель дроби приравниватся к нулю и решается полученное уравнение относительно s); шаг 2 – каждому корню ставится в соответствие простая дробь вида шаг 3 – определяются коэффициенты Mi по одному из вариантов расчета. Первый вариант. Определение Mi с помощью системы уравнений. Все дроби приводятся к одному знаменателю, затем путем сравнения коэффициентов при равных степенях s числителя полученной дроби и числителя исходной определяется система из n уравнений, где n – степень знаменателя (количество корней si и коэффициентов Mi). Решение системы относительно Mi дает искомые коэффициенты. Пример. Декомпозиция дроби из предыдущего примера. В исходной дроби n = 3, поэтому решение уравнения s3 + 5s2 + 6s = 0 дает 3 корня: s0 = 0, s1 = -2 и s2 = -3, которым соответствуют знаменатели простых дробей вида s, (s – s1) = (s + 2) и (s – s2) = (s + 3). Исходная дробь декомпозируется на три дроби:
Далее дроби приводятся к общему знаменателю: = Сравнивая получившуюся дробь с исходной, можно составить систему из трех уравнений с тремя неизвестными (при 2-й степени s в исходной дроби стоит 0, при 1-й стоит 2, свободный член равен 12):
5.М0 + 3.М1 + 2.М2 = 2 à M1 = -4 6.М0 = 12 M2 = 2 Следовательно, дробь можно представить как сумму трех дробей:
Второй вариант. Определение коэффициентов Mi по формулам. Также как и в 1-м варианте необходимо найти корни знаменателя исходной дроби вида - Для нулевого корня si = 0 знаменатель исходной дроби можно записать в виде A(s) = s.A1(s); тогда коэффициент Mi можно определить как - Для ненулевого некратного корня (действительного или комплексного) si:
где A’(s) – производная знаменателя по s. Примечание - Комплексные корни при решении уравнений появляются комплексно-сопряженными парами вида si = ai ± j×wi, где ai – действительныя часть корня, wi – мнимая часть, j – мнимая единица. Поэтому коэффициенты для этих корней также будут комплексно-сопряженными: Mi = ci ± di. То есть достаточно определить коэффициент только для одного корня, для парного корня он будет комплексно-сопряженным. - Для корня si кратности k исходная дробь может быть представлена в виде
данному корню соответствуют k дробей вида
коэффициенты которых определяются по формуле
Пример. Декомпозиция дроби. Рассматривается та же дробь, имеющая три корня: s0 = 0, s1 = -2 и s2 = -3. Для корня s0 = 0 имеем B(s) = 2.s + 12, A1(s) = s2 + 5s + 6,
Для корня s1 = -2 имеем A’(s) = 3.s2 + 10.s + 6 и
Для корня s2 = -3 имеем аналогично
Видно, что коэффициенты Mi, полученные разными методами, совпадают.¨
Пример. Случай обратного преобразования Лапласа при наличии комплексных корней. Изображение выходного сигнала имеет вид
Корни знаменателя включают нулевой корень, действительный и пару комплексных корней: s0 = 0; s1 = - 2,54; s2,3 = - 0,18 ± j*1,20. Изображение Y(s) разбивается на сумму четырех дробей:
Тогда оригинал y(t), согласно таблицам 1.1 и 1.2, имеет вид y(t) = y0(t) + y1(t) + y2,3(t) = M0 + где a и w - действительная и мнимая части пары комплексных корней s2,3, C и D – действительная и мнимая части пары коэффициентов М2 и М3. Для корня s0 = 0:
y0(t) = M0 = 0,85. Для корня s1 = -2,54:
y1(t) = Для корней s2,3 = -0,18 ± j*1,20:
y2,3(t) =2 е-0,18t [-0,34 cos(1,20 t) - 0,24 sin(1,20 t)]. В итоге получаем оригинал: y(t) = 0,85 – 0,18 е-2,54 t – 2 е-0,18 t [0,34 cos(1,20 t) + 0,24 sin(1,20 t)].¨ Передаточные функции
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 4315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |

 Рассмотрим сущность процесса линеаризации на примере сушильного шкафа. Зависимость температуры объекта от подаваемого напряжения в большинстве случаев нелинейна и имеет вид, представленный на рисунке 1.17.
Рассмотрим сущность процесса линеаризации на примере сушильного шкафа. Зависимость температуры объекта от подаваемого напряжения в большинстве случаев нелинейна и имеет вид, представленный на рисунке 1.17.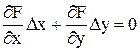 ,
, и
и  - частные производные от F по х и у. Данное уравнение называется уравнением в приращениях, поскольку значения х и у здесь заменены на приращения Dх = х - х0 и Dу = у - у0.
- частные производные от F по х и у. Данное уравнение называется уравнением в приращениях, поскольку значения х и у здесь заменены на приращения Dх = х - х0 и Dу = у - у0.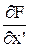 ,
,  ,
, 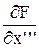 и т.д.). Итоговое уравнение в приращениях будет содержать приращения производных: Dх’ = х’ – х’0, Dх” = х” – х”0, …, Dy’ = y’ – y’0, Dy” = y” – y”0, и т.д.
и т.д.). Итоговое уравнение в приращениях будет содержать приращения производных: Dх’ = х’ – х’0, Dх” = х” – х”0, …, Dy’ = y’ – y’0, Dy” = y” – y”0, и т.д. y = 5
y = 5 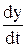 + y
+ y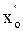 = 0,
= 0, 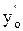 = 0. Для определения недостающего начального условия у0 подставим данные значения в ДУ:
= 0. Для определения недостающего начального условия у0 подставим данные значения в ДУ: = (3у - 8х
= (3у - 8х  = 3*2 - 8*1 = -2,
= 3*2 - 8*1 = -2,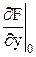 = (3х + 1,5x’ - 1
= (3х + 1,5x’ - 1  = (1,5у
= (1,5у 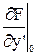 = -5.
= -5. ,
, , (2.1)
, (2.1)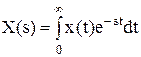 и
и 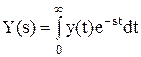 , (2.2)
, (2.2)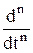 на операторы sn, знаков интегралов
на операторы sn, знаков интегралов 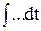 на множители
на множители  , а самих x(t) и y(t) - изображениями X(s) и Y(s).
, а самих x(t) и y(t) - изображениями X(s) и Y(s).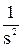

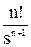
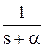

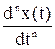
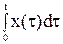
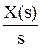
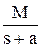
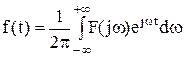 , (2.3)
, (2.3)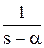 .
.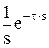 .
.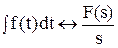 .
. ,
, ,
,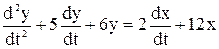
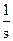 .
.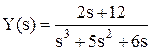 .
.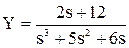 =
= 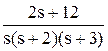 =
= 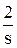 -
- 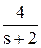 +
+ 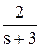 .
. , где Мi – неизвестный коэффициент; если имеет место кратный корень с кратностью k, то ему ставится в соответствие k дробей вида
, где Мi – неизвестный коэффициент; если имеет место кратный корень с кратностью k, то ему ставится в соответствие k дробей вида 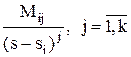 ;
;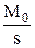 +
+ 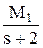 +
+ 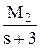 .
. .
.
 М0 + М1 + М2 = 0 M0 = 2
М0 + М1 + М2 = 0 M0 = 2 . Для определения Mi существуют формулы для каждого вида корней:
. Для определения Mi существуют формулы для каждого вида корней: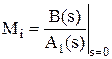 .
.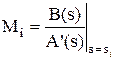 ,
,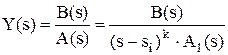 ;
; ,
, .
.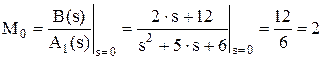 .
.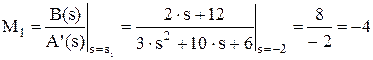 .
. .
. .
. .
.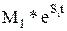 + 2 еat [C . cos(w.t) - D . sin(w.t)],
+ 2 еat [C . cos(w.t) - D . sin(w.t)], ,
,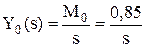 ,
,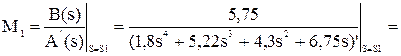 ,
,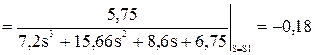 ,
, ,
,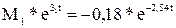 .
. ,
,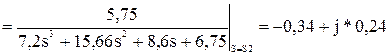 ,
,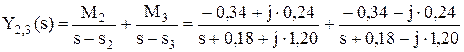 ,
,


