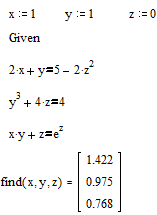Root(Выражение, имя переменной)

Эта функция возвращает значение переменной, при котором выражение равно нулю с заданной точностью. Функция реализует вычисление итерационным методом. Необходимо задать начальное значение переменной. В зависимости от заданного начального приближения к корню находится ближайший корень. Функция root находит только один корень, ближайший к заданному начальному значению. Для отыскания всех корней необходимо задавать различные значения начальных приближений.Функция root может отыскивать и комплексные корни. Недостатком функции root является невозможность решения с ее помощью систем нелинейных уравнений. На рис.61 приведен пример применения функции root. Точность решения задается переменной TOL. По умолчанию задается точность 0,001.Если точность выше 0,001, то требуется изменить количество знаков после запятой при выводе вещественных чисел по команде Format.

 

 

Рис.61. Пример решения нелинейного уравнения с применением функции root

 

2. Решение уравнений полиномиального вида

 

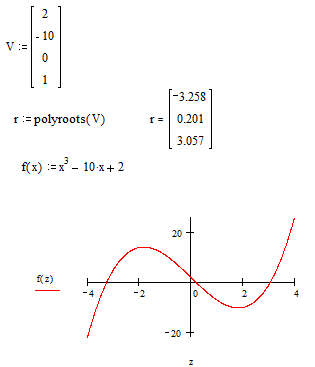
Для поиска корней обычного полинома р(х) степени n MathCad содержит очень удобную функцию

Polyroot(V)

Она возвращает вектор всех корней многочлена (полинома) степени n, коэффициенты которого находятся в векторе V, имеющем длину, равную n+1.

Корни полинома могут быть как вещественными, так и комплексными. Не рекомендуется пользоваться этой функцией, если степень полинома выше пятой-шестой, в этом случае трудно получить малую погрешность вычисления корней.

На рис.62 приведен пример применения функции polyroot.

 

 

Рис.62. Пример решения уравнения полиномиального вида на примере применения функции polyroot

 

3. Символьное решение уравнений

 

Для выполнения символьных вычислений MathCad дополнен символьным процессором, операции которого содержатся в подменю позиции Simbolic главного меню. Можно открыть таблицу символьных операций из математического меню.

Функция

Solve,x

позволяет найти значение обозначенной переменной, при которой содержащее ее выражение становится равным нулю.

На рис.63 приведен пример применения функции solve. Чтобы поставить знак =, нужно одновременно нажать Ctrl и знак = или воспользоваться специальной палеткой для набора знаков.

 

Рис.63. Пример символьного решения нелинейного уравнения с применением функции solve

4. Решение систем линейных уравнений с помощью функции lsolve

 

Для решения систем линейных уравнений в MathCad введена встроенная функция

Lsolve(A,B),

которая возвращает вектор Х для системы линейных уравнений А*Х=В при заданной матрице коэффициентов А и векторе свободных членов В.

На рис.64 приведены примеры применения функции lsolve.

 

Рис.64. Пример символьного решения системы линейных уравнений с применением функции lsolve

5. Решение систем линейных уравнений в матричной форме.

 

Векторные и матричные операторы и функции системы MathCad позволяют решать широкий круг задач линейной алгебры.

Для системы линейных уравнений А*Х=В при заданной матрице коэффициентов А и векторе свободных членов В вектор решения можно получить из очевидного выражения Х=В*А .

На рис.65 приведен пример решения систем линейных уравнений в матричной форме.

Рис.65. Пример матричного решения системы линейных уравнений

 

 

6. Решение нелинейных уравнений и их систем

 

При решении нелинейных уравнений и их систем используется специальный вычислительный блок, открываемый служебным словом-директивой Given, которое набирается с клавиатуры. До начала блока задаются начальные приближения к неизвестным переменным. Внутри блока записывается уравнение или система уравнений. Для решения систем нелинейных уравнений используется одна из двух следующих функций:

find(v1,v2...vn) - возвращает значение одной или нескольких переменных для точного решения;

minerr(v1,v2...vn) - возвращает значение одной или нескольких переменных для приближенного решения.

Между этими двумя функциями существуют принципиальные различия. Первая функция используется, когда решение реально существует (хотя и не является аналитическим). Вторая функция пытается найти максимальное приближение даже к несуществующему решению путем минимизации среднеквадратичной погрешности решения.

На рис. 66 и 67 приведены примеры применения функции find и minerr для решения уравнений и систем уравнений.

Рис.66. Пример решения нелинейных уравнений с помощью функций find и minerr

Рис.67. Пример решения систем нелинейных уравнений с помощью функций find и minerr