
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод ньютона (касательных).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если уравнение
В результате задача определения корня
Итерационный метод решения уравнения, использующий преобразование исходного уравнения к виду (1), называют методом Ньютона. При этом получим следующую рекуррентную формулу
Построим график функции
Найдём точку Тот же результат получим из соотношения (2) при Следует отметить, что при При
где m, M – некоторые положительные константы, для которых
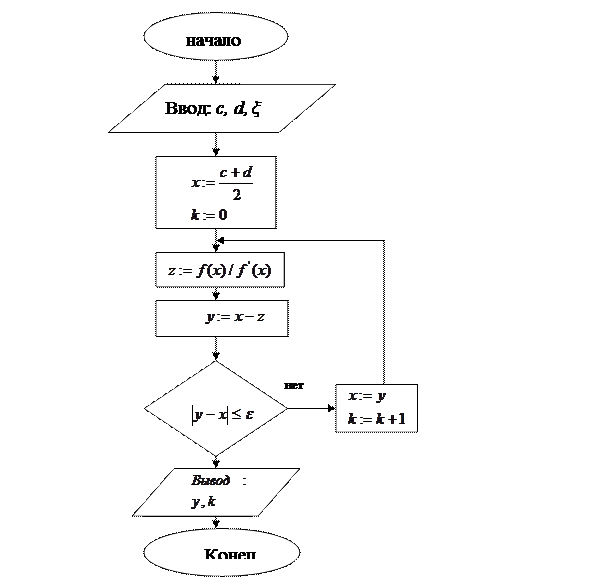
для всех Приведём алгоритм решения уравнения методом Ньютона в виде блок – схемы:
Метод Ньютона обеспечивает более быструю сходимость, чем метод простой итерации. В заключение следует отметить, что при решении нелинейных уравнений
Численные решения СЛАУ. Метод Гаусса. Пусть задана система линейных уравнений Ax=U с плотной матрицей, элементы которой хранятся в оперативной памяти.
Переходим к системе (исключения х1)
Эта операция равносильна умножению Ax=U слева на матрицу
где pi1= aij(1)= aij- Следующий переход к системе (исключения х2)
Это исключения равносильно умножению A1 x= U 1 слева на матрицу Р2:
где pi2= A1 x= U1=> Продолжая этот процесс и так далее, мы придем к легко решаемой системе уравнений с треугольной матрицей An-1х =Un-1
P Q
Где матрица P- нижняя треугольная, а Q- верхняя треугольная. Решение по методу Гаусса сводится к разложению A на произведение двух треугольных матриц. Одна из них
Заметим, что det A=det P*det Q= a11 a22(1) a33(2)… ann(n-1)
Py= U ↓ (y)
Qx= y ↑ (x) Решения по методу Гаусса сводится фактически к решению системы Py= U ↓ При прямом ходе, а затем к решению системы Qx= y ↑ при обратном ходе.
После вычисления прямого хода мы получаем матрицу An-1= Q Метод Холецкого, прогонки приводят к факторизации матрицы A. Метод Холецкого. Пусть дана невырожденная матрица размером N*N (det A≠0) Представим её в виде произведения
k>i bik=0, когда k>i ckj=0 при k>j cjj =1 Из (1) следует aij= Преобразуем эту сумму двумя способами aij=
aij= Отсюда находим bij= cjj= Матрицы B и C найдены, тогда Ax= BCx=U By=U ↓ (y) прямой ход
Cx=y ↑ (x) обратный ход
Лекция 8 Метод прогонки. Решение многих задач для обыкновенных дифференциальных уравнений и уравнений в частных производных приводит к системам линейных уравнений с матрицами специального вида, для решения которых целесообразно применять не общие методы, а методы, использующие специфику полученной системы. Пусть требуется найти решение следующей системы трехточенных уравнений.
Или в векторной форме A
A=
По методу Гаусса A= * = * Факторизация ленточных матриц, т.е. разложение их на произведение двух треугольных матриц A=PQ (нижней и верхней) треугольных матриц может быть произведено так, что P и Q также будут ленточными матрицами. Перейдем к следующей системе (3) yj=pj+1yj+1+qj+1 (3) Где pj+1 и qj+1 неизвестные числа
u1- p2u2 =q2 = u0- p1u1 =q3
Числа pj и qj можно искать из системы (1), т.к. yj-1=pjyj+qj (4) Подставляя (4) в систему (1) получим -aj(pj yj+ qj)+cj yj-bj yj+1=fj (cj-aj pj)yj=bj yj+1 +(fj+ aj qj)
Сравнивая (5) с(3) получим
Из 1 го крайнего условия
Из 2 го крайнего условия
-an yn-1+cnyn=fn
Теперь с помощью (3) получим
Проверка метода прогонки на устойчивость. Поскольку вычисления pj и qj производятся по рекуррентным формулам, то в зависимости от элементов матрицы A: ai, bi, ci, то неизбежны ошибки округления при вычислении по рекуррентным формулам pj и qj. Эти ошибки могут быстро возрастать и сделать вычисления непригодными. Поведение ошибки dpj+1 можно проследить, положив её приближённо равной дифференциалу функции.
Имеем
Прогонка будет устойчивой, если Тогда dpj+1 <dpj Эти неравенства (10) будут выполнены, если, например, положить, что коэффициент матрицы A удовлетворяют следующие условия 0≤ aj≤bj cj≥ aj+bj (11) j= 0< В самом деле
Вообще, проверяется pj+1≤ 1 для j=1,n-1 При этих условиях при вычислении pj+1 накопление ошибки не происходит. Аналогично из равенств
Т.к. при тех же условиях (11) нарастания погрешностей при вычислении q j+1 не происходит.
Лекция 9
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.92.213 (0.007 с.) |

 имеет корень
имеет корень 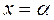 и непрерывную производную
и непрерывную производную 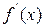 на отрезке
на отрезке 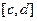 , то функцию
, то функцию 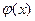 можно выбрать в виде
можно выбрать в виде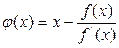 .
.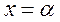 уравнения
уравнения 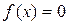 сводится к отысканию корня уравнения
сводится к отысканию корня уравнения . (1)
. (1)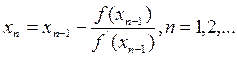 (2)
(2)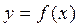 . Уравнение касательной в точке
. Уравнение касательной в точке 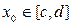 будет иметь вид
будет иметь вид 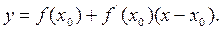

 пересечения этой касательной с осью у. Так как при
пересечения этой касательной с осью у. Так как при 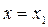
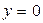 , то
, то 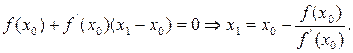
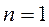 . Следовательно, первое приближение
. Следовательно, первое приближение 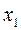 корня можно найти и геометрически с помощью касательной к графику функции
корня можно найти и геометрически с помощью касательной к графику функции 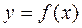 в точке
в точке 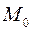 . Аналогичным путём можно построить второе
. Аналогичным путём можно построить второе 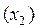 и последующие приближение. Отсюда название метод касательных.
и последующие приближение. Отсюда название метод касательных.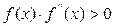 сходимость алгоритма метода Ньютона будет наблюдаться при любых начальных приближениях в интервалах
сходимость алгоритма метода Ньютона будет наблюдаться при любых начальных приближениях в интервалах 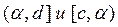 .
.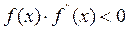 сходимость итерационного процесса будет обеспечиваться при выборе начального приближения из условия
сходимость итерационного процесса будет обеспечиваться при выборе начального приближения из условия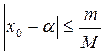 ,
,
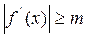 ,
, 
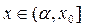 .
.
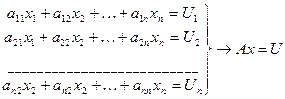
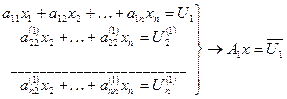
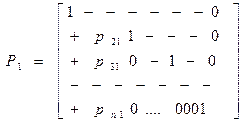
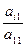 i=2,3…n A1 x= U1à
i=2,3…n A1 x= U1à 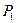 Ax=
Ax= 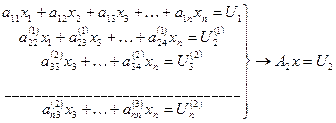
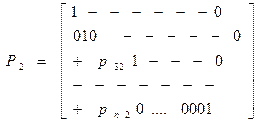
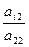 i=3,4…n aij(2)= aij(1) -
i=3,4…n aij(2)= aij(1) - 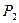 a2j(1)
a2j(1)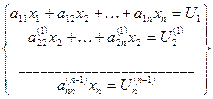
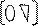 An-1 =
An-1 =
 An-1- верхняя треугольная матрица. Здесь An-1х=Un-1=> =Pn-1Pn-2Ax= Pn-1Pn-2 U, так что A =(Pn-1Pn-2 …P1)-1 An-1х
An-1- верхняя треугольная матрица. Здесь An-1х=Un-1=> =Pn-1Pn-2Ax= Pn-1Pn-2 U, так что A =(Pn-1Pn-2 …P1)-1 An-1х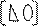

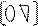
 A = *
A = *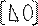 P~ с единицами по главной диагонали и на верхнюю треугольную
P~ с единицами по главной диагонали и на верхнюю треугольную Q~
Q~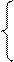
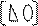 Если представления матрицы A в виде PQ найдены, то решение системы Ax=U сводится к решению двух треугольных систем уравнений.
Если представления матрицы A в виде PQ найдены, то решение системы Ax=U сводится к решению двух треугольных систем уравнений.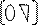 Ax=U=>PQx=U=>
Ax=U=>PQx=U=>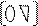
 A=BC (1) A~(aij) B~(bij) C~(cij)
A=BC (1) A~(aij) B~(bij) C~(cij)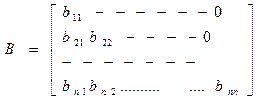

 bik cki
bik cki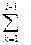 bik cki+ bii cij+
bik cki+ bii cij+ 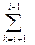 bik cki+ bii cij
bik cki+ bii cij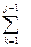 bik ckj+ bij cjj+
bik ckj+ bij cjj+ 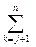 bik ckj=
bik ckj= 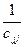
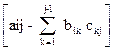 i ≥ j b11=a11 cjj=1
i ≥ j b11=a11 cjj=1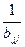
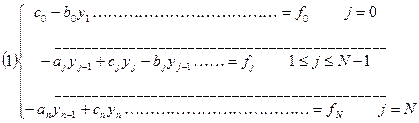
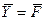 (2)
(2)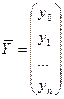
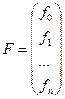
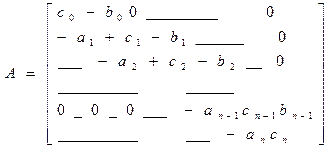
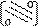
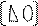
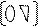

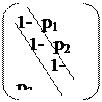

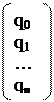
 u0- p1u1 =q1
u0- p1u1 =q1  (5)
(5)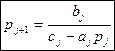
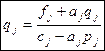 (6)
(6)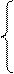
 y0 =p1y1+q1
y0 =p1y1+q1 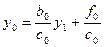 =>
=> 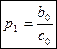
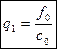 (7)
(7)
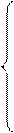 yn-1= pnyn+qn
yn-1= pnyn+qn 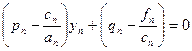
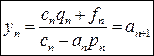 (8)
(8)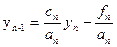
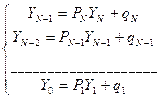
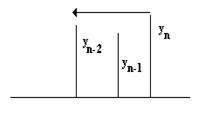
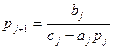
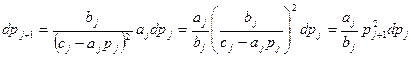 (9)
(9) и
и 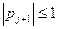 (10)
(10)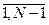
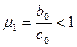
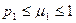 , отсюда
, отсюда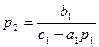 <
< 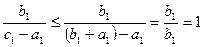
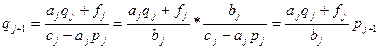 ;
;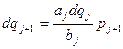 <dqj
<dqj


