
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия параллельности и перпендик-типрямых.Содержание книги Поиск на нашем сайте
Равенство угловых коэф-товявл-ся необходимым и достаточным условием парал-ти двух прямых. Для перпендик-ти прямых необходимо и достаточно, чтобы их угловые коэф-ты были обратны по величине и противоположны по знаку. Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.
19.Кривые второго порядка (окружность, парабола, эллипс, гипербола). Аналитическая геометрия в пространстве. Окружность. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности. Получим уравнение окружности, если известны ее центр и радиус. Окружность радиуса Rс центром в т.
Эллипс. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная. Пусть F1и F2 – фокусы эллипса. Начало O системы координат расположим на середине отрезка F1F2. Ось Ox направим вдоль этого отрезка, ось Oy – перпендикулярно к этому отрезку. Пусть сумма расстояний от точки эллипса до фокусов равна 2a, а расстояние между фокусами – 2c. Тогда в выбранной системе координат эллипс имеет уравнение
Прямоуг-ник со стор 2а и 2в назыв-ся основным прямоуг-ником гиперболы.
Равносторонней гиперболой назыв такую гиперболу, где ее полуоси равны a=b.
Парабола. Мн-во точек, кажд из котор одинаково удалена от данной точки, назыв фокусом и данной прямой, назыв директрисой. Расст-ние от фокуса F до директрисы назыв параметром(р>0).
FM- фокальный радиус т-ки М. О(0;0) – вершина параболы. Т-ма: Уравнение определ либо окр-ть (А=С), эллипс (А*С>0), гиперболу (А*С<0), параболу(А*С=0). Возможный случай вырождения: для эллипса(окр-ти)-в точку или мнимый эллипс(окр-ть); для гиперболы – в пару пересек-сяпрямых; для параболы-в пар парал-ных прямых.
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.54 (0.005 с.) |

 . Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.
. Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю. 
 имеет уравнение
имеет уравнение
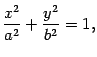 где
где  Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением (12.4), то его осями симметрии служат оси Ox и Oy, начало координат -- центр симметрии.
Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии -- центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины -- большой полуосью эллипса. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины -- малой полуосью. Величина
Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением (12.4), то его осями симметрии служат оси Ox и Oy, начало координат -- центр симметрии.
Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии -- центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины -- большой полуосью эллипса. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины -- малой полуосью. Величина  называется эксцентриситетом эллипса.
Если эллипс задан каноническими уравнениями, то его вершины имеют координаты (-a;0), (a;0),(0;-b),(0;b), большая полуось равна a, малая полуось равна b. Величина c, являющаяся половиной расстояния между фокусами, определяется из формулы (12.5) для величины b, а именно,
называется эксцентриситетом эллипса.
Если эллипс задан каноническими уравнениями, то его вершины имеют координаты (-a;0), (a;0),(0;-b),(0;b), большая полуось равна a, малая полуось равна b. Величина c, являющаяся половиной расстояния между фокусами, определяется из формулы (12.5) для величины b, а именно,  .
Эксцентриситет E эллипса характеризует степень вытянутости эллипса. Чем ближе экцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса 0<E<1.
F1M=r1, F2M=r2 –фокальные радиусы.
r1+r2=2a. r1=a+Ex; r2=a-Ex.
X=
.
Эксцентриситет E эллипса характеризует степень вытянутости эллипса. Чем ближе экцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса 0<E<1.
F1M=r1, F2M=r2 –фокальные радиусы.
r1+r2=2a. r1=a+Ex; r2=a-Ex.
X=  – прямые директрисы.
– прямые директрисы.
 -основное ур-ние эллипса.
-основное ур-ние эллипса.
 .
Гипербола.
Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.
Пусть расстояние между фокусами F1и F2 гиперболы равно 2c, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 2a. Тогда гипербола в выбранной выше системе координат имеет уравнение
.
Гипербола.
Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.
Пусть расстояние между фокусами F1и F2 гиперболы равно 2c, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 2a. Тогда гипербола в выбранной выше системе координат имеет уравнение
 где
где  ,где а – действит полуось, в – мнимая пол-сь.
,где а – действит полуось, в – мнимая пол-сь.

 - асимптоты.
- асимптоты.
 ;
; 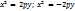 .
.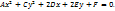 - общурлин 2го порядка.
- общурлин 2го порядка.


