
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С.л.а.у. с прямоугольными матрицами. Теорема Кронекера-Капелли.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема: Для того чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы. Очевидно, что однородная система всегда совместна, поскольку у нее всегда есть тривиальное — нулевое решение. Совместность однородной системы легко получить из теоремы Кронекера-Капелли: добавление столбца правых частей — нулевого столбца, не может увеличить ранг матрицы. Однородной с-мой наз-сясис-ма, свободные члены которой =0. Сис-ма всегда совместна, если определ-ль ≠0. Для совместных систем линейных уравнений верны следующие теоремы. 1. Если ранг матрицы совместной системы равен числу переменных, т.е. r=n, то система имеет единств решение. 2. Если ранг матрицы совместной системы меньше числа переменных, т.е. r<n, то система неопределенная и имеет бесконечное множ-во решений. Сис-ма однородных уравнений. Фундаментальная система решений Система линейных уравнений называется однородной, если все коэффициенты правых частей равны нулю:
Однородная система всегда совместна: она имеет тривиальное решение: Задача ставится о поиске нетривиального решения. Оно не всегда существует. Так, к примеру, если матрицаАсистемы — квадратная и имеет ненулевой определитель, то, согласно теореме Крамера, нетривиальных решений у однородной системы нет. Теорема Кронекера-Капелли утверждает, что условие Сис-малиноднородур им ненулевые решения тогда и только тогда, когда ранг ее м-цыкоэф-тов при переменных меньше числа переменных, т.е. при r(A)<n. Решения сис-мы линур-ний обладают след св-вами: 1) если строка Система линейно независимых решений Т-ма:если рангr м-цыкоэф-тов при переменных сис-мы линоднородн уравнений меньше числа переменных n, то всякая фундамент сис-ма решений сис-мы состоит из n – rрешений. Поэтому общее решсис-мы линоднороднуравн им вид: Общее решение сис-мы mлинур с n переменными равно сумме общего решсоответ-щей ей сис-мы однор-ныхлинур и произв-го частного решения этой сис-мы. Векторы. Линейные операции над векторами. Вектором называется направленный отрезок. Если начало вектора находится в точке А, а конец – в точке В, то вектор обозначается АВ. Если же начало и конец вектора не указываются, то его обозначают строчной буквой латинского алфавита a, b, c,…. Через BA обозначают вектор, направленный противоположно вектору АВ. Вектор, у которого начало и конец совпадают, называется нулевым и обозначается ō. Его направление является неопределенным. Длиной или модулем вектора называется расстояние между его началом и концом. Записи |АВ| и |a| обозначают модули векторов АВ и a. Векторы называются коллинеарными, если они параллельны одной прямой, и компланарными, если они параллельны одной плоскости. Два вектора называются равными, если они коллинеарны, одинаково направлены и равны по длине. К линейным операциям над векторами относятся: 1)умножение вектора на число (Произведением вектора a и числа α называется вектор, обозначаемый α∙a. (или наоборот a∙α), модуль которого равен |α a| =|α||a|, а направление совпадает с направлением вектора a, если α>0, и противоположно ему, если α< 0.) а*(вс) = (ав)*с и а*(в + с) = ав + ас. 2)сложение векторов: (а + в) + с = а + (в + с): Пр-ло
Пр-лопараллелогр-ма:
3)вычитание векторов: а – в = а + (-в): Проекции вектора на ось. Ось – прямая, им направление. Числов ось – прямая, с нач отсчета и единичным масштабом. Проекции сущ 2 вида: геометр-кая и алгебр-кая. Проекция вектора на ось равна произведению длины вектора
При умножении вектора на число его проекция на ось также умножается на это число. Проекция суммы векторов на ось равна сумме проекций слагаемых:
Свойства проекций:1) пр Проекция в-ра на ось положит-на (отриц-на), если век-р образует с осью острый (тупой) угол и равна 0, если этот угол прямой. Проекции равн век-ров равны м/у собой. 2) проекция суммы неск век-ров на одну и ту же ось = сумме их проекций на эту ось. 3) при умножении
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.72 (0.007 с.) |


 .
. является и достаточным для существования нетривиального решения.
является и достаточным для существования нетривиального решения.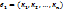 - решение сис-мы, то и строка
- решение сис-мы, то и строка  -также реш этой сис-мы. 2) если строки
-также реш этой сис-мы. 2) если строки  -решсис-мы, то при люб
-решсис-мы, то при люб  их линейная комбинация
их линейная комбинация  – также реш этой комбинации.
– также реш этой комбинации. назыв-ся фундаментальной, если кажд решение сис-мы яв-сялин комбинацией решений
назыв-ся фундаментальной, если кажд решение сис-мы яв-сялин комбинацией решений  .
. -ка:
-ка: на косинус угла между вектором и осью:
на косинус угла между вектором и осью:


 на l = произв
на l = произв  на cos
на cos  м/у вектором и осью.
м/у вектором и осью. 
 его проекция на ось также умнож-ся на это число:
его проекция на ось также умнож-ся на это число: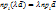 .
.


