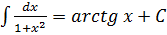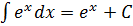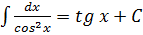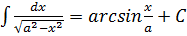Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1.1. Матрицы и определителиСодержание книги
Поиск на нашем сайте
РАЗДЕЛ 1. ЛИНЕЙНАЯ АЛГЕБРА Тема 1.1. Матрицы и определители Написание рефератов, докладов
Создание презентаций
Тема 1.2. Система линейных уравнений Исследовательская работа. Решение задач Линейная однородная система n уравнений с n неизвестными. Метод Гаусса. Исследовать системы линейных уравнений, для совместных систем найти общее и одно частное решение: 1. 3. 5. 7. 9.
Вопросы для самопроверки 1. Дайте определение системы m линейных уравнений с n неизвестными 2. Что называют решением системы m линейных уравнений с n неизвестными? 3. Какая система называется совместной? 4. Какие системы называются эквивалентными? 5. Что значит исследовать систему линейных уравнений? 6. В чем заключается суть метода Гаусса для исследования систем линейных уравнений? 7. К системе линейных уравнений с n неизвестными дописали произвольное уравнение с m неизвестными. Как при этом изменится множество решений системы? 8. Из несовместной системы линейных уравнений удалили какое-то одно уравнение. Будет ли полученная система совместной? 9. Что можно сказать о множестве решений системы линейных уравнений, ранг r(A) матрицы этой системы и ранг r(A 10. Может ли частное решение системы линейных уравнений совпадать с её общим решением? РАЗДЕЛ 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦЦИИ ОДНОЙ ПЕРЕМЕННОЙ Основные положения теории пределов 1. Первый замечательный предел:
следствие из первого замечательного предела:
2. Второй замечательный предел:
следствие из второго замечательного предела:
3. Раскрытие неопределенности вида Первое правило Лопиталя: Если
когда последний предел существует (конечный или бесконечный) 4. Раскрытие неопределенности вида Второе правило Лопиталя: Если
когда последний предел существует (конечный или бесконечный) 5. Неопределенности вида 0 • Неопределенности вида 0 •
сводятся к неопределенности вида 0• Например, 6. Эквивалентными называются бесконечно малые, предел отношения которых равен единице. Отношение двух бесконечно малых величин можно заменить отношением эквивалентных величин, например,
7. При решении многих задач используются следующие эквивалентности, верные при x→0:
Операции над пределами функций Пусть функции ⨍(x) и
Тогда: 1) 2) 3) 4) Тема 2.1. Функции, пределы, непрерывность Написание рефератов, докладов - Непрерывность некоторых элементарных функций
Вопросы для самопроверки 1. Сформулируйте определение непрерывности функции в точке 2. В чем различие между понятиями непрерывности функции и пределов функции в точке 3. Почему из непрерывности функции слева и справа в точке 4. Сформулируйте теорему об арифметических действиях над непрерывными функциями. 5. Докажите, что функция f(x) 6. Почему можно утверждать, что функция f(x)= 7. Какие точки называются точками разрыва функции? 8. Дайте определения точек разрыва первого и второго рода. 9. Укажите, в какой точке и какого рода разрыв имеет функция f(x)=
Исследовательская работа. Решение задач Некоторые нестандартные ситуации при вычислении пределов функций. Упражнения. Найдите: 1. 2. 4. 6. 8. 10. 12. 14. (Указание: сделать подстановку x-1=y.) (Отв. 3.) 16. 18. 19. 20. 21. 22. 24. Контрольные задачи к разделу Найдите пределы: 2.1.1. 2.1.3. 2.1.5. 2.1.7. 2.1.9. 2.1.11. 2.1.13. 2.1.15. 2.1.17. 2.1.19 2.1.21.
Найдите пределы (Указание: воспользоваться сведением к первому замечательному пределу)
2.1.23. 2.1.25 2.1.27. 2.1.29. Найдите пределы(Указание: воспользоваться сведением ко второму замечательному пределу):
2. 1. 32.
2. 1. 34.
Вопросы для самопроверки 1. Сформулируйте два определения предела функции. Что означает эквивалентность этих определений? 2. Приведите пример функции, не имеющей предела в данной точке. 3. При каких условиях из существования предела функции и наоборот? 4. Существует ли 5. Сформулируйте два определения предела функции при x 6. Докажите, что 7. Что означает записи: x 8. В каких случаях говорят о наличии неопределенности вида 9. Что означает слова «неопределенность раскрыта»? 10. Почему x 11. Сформулируйте теоремы о пределах функций. 12. Докажите первый и второй замечательные пределы. 13. Сформулируйте определение бесконечно малой функции и бесконечно большой. Приведите примеры. 14. Какова связь между понятиями предела функции и бесконечно малой функцией? 15. Что означают записи: 16. Какова связь между бесконечно малой и бесконечно большой функциями? 17. В каких случаях говорятся о наличии неопределенности вида Таблица производных элементарных функций
Правила дифференцирования
Вопросы для самопроверки 1. Дайте определение производной функции y=f(x) в точке 2. Каков геометрический смысл производной функции y=f(x) в точке 3. Дайте определение касательной к графику функции y=f(x) в точке 4. Каков физический смысл производной функции y=f(x) в точке 5. Может ли функция, имеющая производную в точке, быть непрерывной в этой точке? 6. Дайте определение дифференциала функции в точке 7. Каков геометрический смысл дифференциала? 8. Сформулируйте теорему о производной сложной функции. ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ Таблица основных интегралов I II III IV V VI VII VIII IX X XI XII XIII XIV РАЗДЕЛ 1. ЛИНЕЙНАЯ АЛГЕБРА Тема 1.1. Матрицы и определители
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.100.233 (0.009 с.) |

 Базис в пространстве;
Базис в пространстве;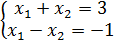 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 
 ,
, 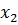 , …,
, …,  .
. расширенной матрицы равны нулю?
расширенной матрицы равны нулю?
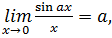 a
a  R
R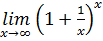 =℮
=℮  =℮
=℮ 
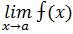 =
= 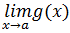 =0, то
=0, то =
= 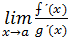

 =
= 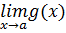 =
=  то
то
 ,
,  ,
,  ,
,  ,
,  и их раскрытие
и их раскрытие и
и  могут быть сведены путем алгебраических преобразований к неопределенностям вида
могут быть сведены путем алгебраических преобразований к неопределенностям вида  и
и  =
= 




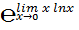 =
=  =1
=1
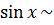 x, 1
x, 1 

 ,
, 


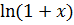
 1
1  (в частности,
(в частности, 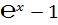


 .
. (x) определены в некоторой окрестности точки
(x) определены в некоторой окрестности точки  и, кроме того,
и, кроме того,
 = A,
= A, = = B.
= = B. = A
= A  B
B = A • B
= A • B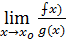 =
=  (при условии B≠0)
(при условии B≠0) =
= 

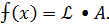
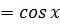 непрерывна в любой точке x.
непрерывна в любой точке x. непрерывна на всей числовой прямой?
непрерывна на всей числовой прямой?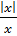 .
. . (Отв. 10.)
. (Отв. 10.) . (Отв.
. (Отв.  .) 3.
.) 3.  . (Отв. 1.)
. (Отв. 1.)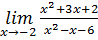 . (Отв.
. (Отв.  .) 5.
.) 5. 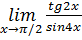 . (Отв.
. (Отв.  .)
.) . (Отв.
. (Отв.  .) 7.
.) 7.  . (Отв.
. (Отв.  . (Отв.
. (Отв.  . (Отв. 4.)
. (Отв. 4.) . (Отв. 2.) 11.
. (Отв. 2.) 11. 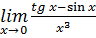 . (Отв.
. (Отв.  .)
.) . (Отв. 14.) 13.
. (Отв. 14.) 13.  . (Отв.
. (Отв.  . (Отв. 9.) 15.
. (Отв. 9.) 15. 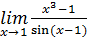 .
. . (Отв.
. (Отв.  .) 17.
.) 17.  . (Отв. 3.)
. (Отв. 3.) . (Отв.
. (Отв.  (
(
 ). (Отв. 3.)
). (Отв. 3.) (
(
 ). (Отв.
). (Отв. 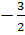 .)
.) (x
(x  ). (Отв.
). (Отв.  .)
.) ). (Отв. 0.) 23.
). (Отв. 0.) 23.  x ctg x. (Отв. 1.)
x ctg x. (Отв. 1.)
 sin
sin  . (Отв. X.) 25.
. (Отв. X.) 25. 
 (5
(5  +2x-1). 2.1. 2.
+2x-1). 2.1. 2.  .
. . 2.1.4.
. 2.1.4.  .
.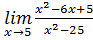 . 2.1.6.
. 2.1.6.  .
.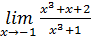 . 2.1.8.
. 2.1.8.  .
. . 2.1.10.
. 2.1.10. 
 .
. . 2.1.12.
. 2.1.12.  .
. . 2.1.14.
. 2.1.14.  .
. . 2.1.16.
. 2.1.16.  .
. . 2.1.18.
. 2.1.18.  .
. . 2.1.20.
. 2.1.20.  .
. 2.1.22.
2.1.22.  x).
x). 2.1.24.
2.1.24.  .
. . 2.1.26.
. 2.1.26.  .
. . 2.1.28.
. 2.1.28.  .
. ctgx. 2.1.30.
ctgx. 2.1.30.  .
. (1+
(1+  , k
, k 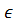 R;
R; ;
; (
( 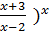
 .
. 
 , x
, x 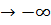 и x
и x  ?
? или
или  ?
? при x
при x  f(x)=+
f(x)=+  ,
, 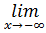 f(x)=+
f(x)=+  (
( )
) 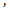 =
=  )
)  (
( )
)  (
( )
)  (
( )
)  (
( (tg x)
(tg x)  =
=  (ctg x)
(ctg x) 

 (arccos x)
(arccos x)  (arctg x)
(arctg x)  (arcctg x)
(arcctg x)  (sh x)
(sh x)  (cth x)
(cth x) 
 (x +
(x +  )
)  = 0
= 0
 u
u  v
v  2
2
 v
v  =
= 
 ; f(
; f(