
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Основы аналитической геометрии на плоскостиСодержание книги
Поиск на нашем сайте
Пояснительная записка Методические рекомендации по выполнению контрольной работы по математике реализуют государственные требования к содержанию и уровню подготовки выпускников обучающихся заочно по специальности «Социально-культурный сервиз и туризм» (230500) в условиях действия государственного образовательного стандарта высшего профессионального образования, оказание помощи студентам-заочникам в организации их самостоятельной работы над изучением учебного материала. 1. Цели дисциплины: § сформировать у студента навыки математического мышления, заключающиеся в умении применять математические методы для изучения закономерностей природы и общества. Полученные знания будут способствовать повышению общей культуры, выработке умений проводить математические исследования в образовательном учреждении, находить оптимальные пути достижения цели, преодоления профессиональных трудностей. 2. Задачи дисциплины: § изучение математики вооружает студентов основами математических знаний, умений и навыков в объеме, необходимом для повседневной практики, для усвоения экономических предметов, а также для дальнейшего повышения квалификации путем самообразования. 3. Место дисциплины в учебном плане Программа курса «Математика» разработана для студентов, чья компетентность и культура органичными составными частями войдут в структуру будущей профессиональной деятельности специалиста по сервисному обслуживанию и туризму. Математика будет способствовать развитию умения учиться, культуры умственного труда, самообразования в профессиональной сфере. 4. Требования к уровню освоения содержания дисциплины § знать основные понятия из аналитической геометрии на плоскости: прямоугольная система координат, уравнения прямых линий, линии второго порядка; § знать понятия матричной алгебры: матрица, определитель; § знать понятие предела, производной, дифференциала, интеграла, дифференциального уравнения, ряда, вероятности, случайной величины, выборочной средней, дисперсии, среднего квадратического отклонения; § иметь представление о современных математических методах, которые применяются к экономическим задачам; § уметь находитьпростейшиепределы, производные, дифференциалы, интегралы, вероятность появления случайного события, выборочную среднюю, дисперсию, среднее квадратическое отклонение; § уметь анализировать функции истроить схематично графики; § уметьрешать простейшие дифференциальные уравнения. 5. Аннотация к методическим рекомендациям Методические рекомендации по выполнению контрольной работы по математике содержат программу дисциплины «Математика», которая предусматривается знакомство с элементами аналитической геометрии и линейной алгебры, с основами математического анализа, теорией вероятностей и математической статистики. Имеются вопросы и упражнения для самопроверки, вопросы для подготовки к экзамену, перечень рекомендуемой литературы, контрольная работа и методические указания по выполнению заданий контрольной работы.
Содержание дисциплины Раздел 1. Основы аналитической геометрии на плоскости Тема 1.1. Уравнение прямых линий Прямоугольная система координат. Расстояние между двумя точками на плоскости. Общее уравнение прямой и его частные случаи. Уравнение прямой с угловым коэффициентом. Уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом. Уравнение прямой, проходящей через две точки. Взаимное расположение прямых. Угол между прямыми, условие параллельности и перпендикулярности прямых. Нормальное уравнение прямой. Расстояние от точки до прямой. Основная литература: [1-5, 8]. Дополнительная литература: [1-4, 6]. Тема 1.2. Линии второго порядка: эллипс, гипербола, парабола Основная литература: [1-5, 8]. Дополнительная литература: [1-4].
Раздел 2. Элементы линейной алгебры Тема 2.1. Матрицы и определители Матрицы, линейные операции над матрицами, умножение матрица. Обратная матрица. Квадратные матрицы, их определители. Вычисление определителей второго и третьего порядков. Миноры и алгебраические дополнения элементов определителя. Теоремы о разложении определителя по элементам строк (столбцов). Понятие о ранге матрицы. Тема 2.2. Решение систем линейных уравнений Решение систем трех линейных уравнений с тремя неизвестными, используя метод Крамера, метод обратной матрицы. Основная литература: [1-5, 8]. Дополнительная литература: [3– 4,6].
Раздел 3. Математический анализ Тема 3.1. Дифференциальное исчисление и его применение Функция. Предел функции одной переменной. Основные теоремы для пределов. Первый и второй замечательные пределы. Бесконечно малые и бесконечно большие функции. Неопределенности вида 0 / 0 и ¥ / ¥. Методы нахождения пределов. Понятие производной, ее геометрический и механический и смысл. Дифференциал функции, его свойства. Применение дифференциала в приближенных вычислениях. Формулы дифференцирования основных элементарных функций. Правила дифференцирования суммы, разности, произведения, частного. Производные высших порядков. Понятие экстремумов, необходимые и достаточные условия экстремумов. Правило исследования функции на экстремум. Признаки выпуклости и вогнутости функции. Необходимые и достаточные условия перегиба. Правило исследования функции на выпуклость, вогнутость. Точка перегиба. Асимптоты функции, их виды и нахождение. Общая схема полного исследования функции. Основная литература: [1-5, 8]. Дополнительная литература: [1-4, 6]. Тема 3.2. Интегральное исчисление Первообразная функция. Неопределенный интеграл, его свойства. Таблица интегралов. Методы интегрирования: непосредственное, замена переменной, интегрирование по частям. Определенный интеграл как предел интегральной суммы, его основные свойства. Формула Ньютона-Лейбница для вычисления определенного интеграла. Методы интегрирования заменой переменной и по частям в определенном интеграле. Приложения интеграла к вычислению площадей плоских фигур. Основная литература: [1-5, 8]. Дополнительная литература: [1- 4, 6]. Тема 3.3. Дифференциальные уравнения Понятие дифференциального уравнения. Дифференциальное уравнение первого порядка с разделяющимися переменными, его общее и частное решение. Однородные уравнения первого порядка. Линейное дифференциальное уравнения первого порядка. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Основная литература: [5, 8]. Дополнительная литература: [1-4, 6]. Тема 3.4. Ряды Понятие числового ряда. Сходящиеся и расходящиеся числовые ряды. Необходимый признак сходимости числового ряда. Ряды с неотрицательными членами. Признаки сходимости: признак сравнения, признак Даламбера, интегральный признак. Знакопеременные ряды. Абсолютная и условная сходимости рядов. Признак сходимости знакопеременного ряда. Степенные ряды. Интервал сходимости. Разложение функции в степенные ряды. Ряд Маклорена. Ряд Тейлора. Ряды Фурье. Основная литература: [4, 5]. Дополнительная литература: [2, 4].
Раздел 4.Теория вероятностей и математическая статистика Тема 4.1. Основные понятия и теоремы теории вероятностей Испытания, события, виды событий, система элементарных событий. Классическое определение вероятности. Относительная частота появления события. Примеры вычисления вероятностей. Теоремы сложений вероятностей несовместимых и совместимых событий. Теоремы умножения вероятностей независимых и зависимых событий. Противоположенные события. Вероятность появления хотя бы одного из независимых событий. Формула полной вероятности. Формула Байеса. Повторение независимых испытаний. Формула Бернулли. Основная литература: [4 –7]. Дополнительная литература: [5]. Аналитическая геометрия Даны координаты вершин треугольника АВС: А(- 2; 7), В(10; - 2), С(8; 12). Построить чертеж и найти: а) длину стороны АВ; б) уравнение высоты, проведенной из вершины С и ее длину; в) уравнение медианы, проведенной из вершины С; г) уравнение прямой, проходящей через вершину С параллельно стороне АВ; д) площадь треугольника. На прямоугольной системе координат строим чертеж.
Рис. 1. Чертеж к задаче по аналитической геометрии а) для нахождения длины АВ используем формулу: ℓ2AB = (X2 – X1)2 + (Y2 – Y1)2, где X1 = – 2, Y1 = 7, X2 = 10, Y2 = – 2 ℓAB = б) для составления уравнения прямой АВ воспользуемся формулой (Y – Y1) /(Y2 – Y1) = (X – X1) /(X2 – X1) => (Y – 7) /(– 9) = (X – 2) / 12 => 12Y – 84 = – 9X – 16 => Y = – (3/4)X + 11/2, где kAB = – ¾ Уравнение высоты СД найдем: Y – YС = kСД (X – XС) , где kСД = – ℓ/ kAB = 4/3, Y = (4/3)X + 4/3 Для нахождения ℓСД необходимо знать координаты точки Д, которые можно найти, решив систему уравнений:
Точка Д имеет координаты (2; 4), а ℓСД = 10. в) для нахождения медианы СМ определим координаты точки М, как середины отрезка АВ: М (4; 2,5). Будем иметь: (Y – YМ) /(YС – YМ) = (X – XМ) / (XС – XМ) => (Y – 2,5) / 9,5 = (X – 4) / 4 => 4Y – 10 = 9,5X – 38 => Y = (19/8)X – 7 г) найдем уравнение прямой линии, проходящей через точку С параллельно стороне АВ. Используем уравнение: Y – YС = kАД (X – XС), где kАД = – 3/4, Y = – (3/4)X + 18 д) площадь S треугольника АВС равна: S = (1/2) ℓAB × ℓCД = 75 (кв. ед.) Вопросы и упражнения для самоконтроля: Формула нахождения расстояние между двумя точками. 1. Что называется медианой? 2. Что называется высотой? 3. Записать условие перпендикулярности и параллельности двух прямых. 4. Уравнение прямой линии с угловым коэффициентом. 5. Уравнение прямой линии в отрезках 6. Уравнение прямой линии, проходящей через две точки. 7. Даны координаты вершины треугольника АВС. Построить чертеж и найти: а) длину стороны ВС; б) уравнение высоты, проведенной из вершины А и ее длину; в) уравнение медианы, проведенной из вершины А; г) уравнение прямой, проходящей через вершину А параллельно стороне ВС; д) площадь треугольника.
а) А(0; 2), В(4; 4), С(8; 2) б) А(2; 5), В(- 6; - 2), С(7; 3) Пределы функций Раскрытие неопределенностей вида 0 / 0 и ¥ / ¥ Пример 1. Найти Решение: Имеем неопределенность вида 0 / 0. Необходимо избавится от неопределенности. Для этого разложим числитель на множители и сократим на общий множитель (Х + 2), который обращает в нуль знаменатель и числитель дроби. Получим:
Так как знаменатель теперь не равен нулю, то неопределенность 0 / 0 ликвидирована. Применяя теоремы для пределов, окончательно находим
Пример 2. Найти
Решение: Имеем неопределенность вида 0 / 0. Необходимо уйти от неопределенности. Для этого применим первый замечательный предел
Пояснение: вынести постоянный множитель 2 за знак предела. Под пределом числитель и знаменатель умножим на 4, вынести множитель 4 и применить первый замечательный предел. Пример 3. Найти Решение: Имеем неопределенность вида
Замечание: Пример 4. Найти Решение: Имеем неопределенность вида ¥ / ¥. Разделим на X2 числитель и знаменатель дроби, а затем, применив теоремы для пределов, получим
Вопросы и упражнения для самоконтроля: 1. Дайте определение предела функции в точке. 2. Основные теоремы для пределов. 3. Первый и второй замечательные пределы. 4. Что такое неопределенности в математике, их виды? 5. Методы нахождения пределов 6. 7. 8. 9. Применение производной Дифференциальные уравнения Пример 11. Решить дифференциальное уравнение первого порядка dY / (Х 3 – 6) - Y dX = 0, Y = 1 при X = 0 Решение: 1. Это дифференциальное уравнение с разделяющимися переменными. Разделим переменные. Для этого, используя алгебраические преобразования, соберем в одной части уравнения X, dX, а в другой – Y, dY. dY / Y = (Х 3 – 6) dX 2. Интегрируем левую и правую части, полученного уравнения.
3. Результат интегрирования дает общее решение дифференциального уравнения. ln Y = Х 4 / 4 – 6X + C, где С – константа интегрирования. 4. Найдем частное решение. Для этого в общее решение подставим начальные условия (Y = 1 при X = 0) и найдем константу интегрирования С. Константа интегрирования С = 0. Частное решение запишется в виде ln Y = Х4 / 4 – 6X или Y = exp (Х4 / 4 – 6X) Ответ: Y = exp (Х4 / 4 – 6X). Пример 12. Решить однородное дифференциальное уравнение второго порядка с постоянными коэффициентами Y11 - 6 Y1 + 9Y = 0 Решение: Составляем характеристическое уравнение. k2 - 6 k + 9 = 0 Решая это квадратное уравнение, находим k1 = k2 = 3 (корни равные). 1. Если корни равные, то общее решение запишется Y = (C1 + C2 X) e3X Вопросы и упражнения для самоконтроля: 1. Какие уравнения называются дифференциальными? 2. Дайте определение дифференциального уравнения первого порядка. 3. Дайте определение общего решения дифференциального уравнения первого порядка. 4. Дайте определение частного решения дифференциального уравнения первого порядка. 5. Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. 6. Решить дифференциальные уравнения и найти частное решение (X + 1)2 dY - (Y - 2)3 dX = 0, Y = 0 при X = 0; (X Y + X) dX + (Y X + Y) dY = 0, Y = 1 при X = 0. 7. Решить однородные дифференциальные уравнения второго порядка с постоянными коэффициентами а) Y11 - 2 Y1 + 4Y = 0; б) Y11 - 2Y1 = 0 Интервальная оценка Пример 15. Найти доверительный интервал для оценки неизвестного математического ожидания μнормального распределения с надежностью 0,95, зная выборочную среднюю XB =14, объем выборки n = 36и среднее квадратичное отклонение sx = 6. Интервальная оценка определяется двумя числами - концами интервала, покрывающего оцениваемый параметр. Интервальной оценке ставится в соответствие вероятность (доверительная вероятность или надежность g), с которой эта оценка накроет неизвестный параметр. Доверительным называют интервал, который с заданной надежностью g покрывает неизвестный параметр. Интервальной оценкой с заданной надежностью g математического ожидания μ нормально распределенного количественного признака X по выборочной средней XB при известном среднем квадратическом отклонении sx генеральной совокупности служит доверительный интервал XB - t (sx / где t (sx / n - объем выборки, t - значение аргумента функции Лапласа Ф(t) (см. приложение 2 в основной литературе [5], [6]), при котором Ф(t) = g / 2. Запишем доверительный интервал: XB - t (sx / Все величины, кроме t, известны. Найдем t из соотношения Ф(t) = 0,95 / 2 = 0,475. По таблице приложения 2 (см. основную литературу [5], [6]) находим t = 1,96. Подставив данные, получим искомый доверительный интервал 12,04 < μ < 15,96 Вопросы и упражнения для самоконтроля: 1. Что такое дискретные случайные величины? 2. Закон распределения дискретных случайных величин. 3. Математическое ожидание дискретной случайной величины, основные свойства. 4. Дисперсия дискретной случайной величины, основные свойства. 5. Среднее квадратическое отклонение дискретной случайной величины. 6. Непрерывные случайные величины. 7. Нормальный закон распределения (закон Гаусса). 8. Что такое выборочная средняя? 9. Что такое выборочная дисперсия? 10. Что такое интервальная оценка? 11. Что такое доверительная вероятность? 12. Интервальная оценка. 13. Выборка задана в виде распределения частот: Xi 4 6 7 ni 20 30 50 Найти распределение относительных частот. Вычислить выборочную среднюю и дисперсию. 14. Выборка задана в виде распределения частот: Xi 2 5 10 ni 5 7 8 Найти распределение относительных частот. Вычислить выборочную среднюю и дисперсию. 15. Найти доверительный интервал для оценки неизвестного математического ожидания μнормального распределения с надежностью 0,95, зная выборочную среднюю XB = 15, объем выборки n = 49и среднее квадратичное отклонение sx = 8. 16. Найти доверительный интервал для оценки неизвестного математического ожидания μ нормального распределения с надежностью 0,95, зная выборочную среднюю XB =10, объем выборки n = 25и среднее квадратичное отклонение sx = 4. Вопросы для подготовки к экзамену 1. Прямоугольная система координат. Расстояние между двумя точками. 2. Уравнение прямой линии с угловым коэффициентом. 3. Уравнение прямой линии отрезка. 4. Уравнение прямой линии, проходящей через две точки. 5. Условие параллельности и перпендикулярности двух прямых. 6. Определители второго и третьего порядка. 7. Минор и алгебраическое дополнение. Разложение определителя по строке или столбцу. 8. Матрица. Основные операции над матрицами. 9. Решение систем линейных алгебраических уравнений по формулам Крамера. 10. Решение систем линейных алгебраических уравнений методом обратной матрицы. 11. Предел функции, свойства пределов. Способы вычисления пределов. Неопределенности вида 0/0 и 12. Первый и второй замечательные пределы. 13. Производная функции, ее механический и геометрический смысл. Производные элементарных функций. Основные правила дифференцирования. Производная сложной функции 14. Бесконечно малые и бесконечно большие функции, их свойства. 15. Дифференциал функции, его свойства. Применение дифференциалов для приближенных вычислений. 16. Асимптоты графика функций. Нахождение асимптот. 17. Интервалы возрастания и убывания функции 18. Интервалы выпуклости и вогнутости. Точка перегиба 19. Экстремумы. Нахождение экстремумов. 20. Общая схема исследования функций и построение их графиков. 21. Неопределенный интеграл. Свойство интеграла. Таблица основных интегралов. Непосредственное интегрирование. 22. Интегрирование методом замены переменной. 23. Интегрирование по частям. 24. Определенный интеграл, его свойства. Формула Ньютона - Лейбница. 25. Вычисление площадей плоских фигур. 26. Предмет теории вероятностей. Случайные события. Виды случайных событий. Классическое определение вероятности. Свойства. 27. Теорема сложения вероятностей несовместных событий. Противоположное событие. 28. Произведение событий. Условная вероятность. Теорема умножения вероятностей. 29. Независимые события. Теорема умножения для независимых событий. 30. Вероятность появления хотя бы одного события. 31. Формула полной вероятности. Вероятность гипотез. Формула Байеса. 32. Повторные испытания. Формула Бернулли. 33. Дискретные случайные величины. Закон распределения вероятностей дискретных случайных величин. 34. Математическое ожидание дискретной случайной величины. Свойства математического ожидания. 35. Дисперсия дискретной случайной величины. Формула для вычисления дисперсии. Свойства дисперсии. Среднее квадратическое отклонение. 36. Определение функции распределения. Свойства функции распределения. График функции распределения. 37. Определение плотности распределения вероятностей непрерывной случайной величины. Вероятность попадания непрерывной случайной величины в заданный интервал. Нахождение функции распределения по известной плотности распределения. Свойства плотности распределения. 38. Нормальное распределение вероятностей непрерывной случайной величины. Влияние параметров нормального распределения на форму нормальной кривой. Вероятность попадания в заданный интервал нормальной случайной величины. Задание для контрольной работы и методические рекомендации по ее выполнению Студенту-заочнику, во-первых, необходимо ознакомиться с содержанием программы, во- вторых, следует выбрать один учебник в качестве основного и придерживаться его при изучении всего курса. Требование к выполнению и оформлению контрольной работы: 1. Контрольная работа выполняется в тетради чернилами любого цвета, кроме красного, оставляются поля 3-4 см с левой стороны страницы для замечаний рецензента. Следует пронумеровать страницы. 2. На обложке тетради должны быть ясно написаны фамилия, имя и отчество студента, учебный номер (шифр), номер контрольной работы, название дисциплины. Следует указать дату отсылки работы в учебное заведение и адрес студента. 3. Условие задачи должны быть обязательно переписаны полностью в тетрадь. Решение задач необходимо располагать в порядке номеров, указанных в задании, номера заданий следует указывать перед условием. Каждую задачу надо начинать с новой страницы. Контрольная работа, которая содержит не все задания, а также содержащие задачи не своего варианта, не будет зачтена. 4. При оформлении записей в тетради необходимо выполнять требования: а) соблюдать абзацы, всякое новое высказывание следует начинать с красной строки, в конце выполнения задания записывается ответ; б) формулы, определения нужно выделять в отдельные строки, чтобы сделать их более обозримыми; в) необходимо правильно употреблять математические символы. 5. Решение задач должно сопровождаться краткими, но достаточно обоснованными пояснениями. 6. Чертежи следует выполнять аккуратно карандашом с использованием чертежных инструментов. 7. В конце работы следует указать литературу, которой пользовались. 8. Если в работе допущены недочеты и ошибки, то в кратчайший срок студент должен исправить все замечания, которые указал рецензент, в этой же тетради. 9. Контрольная работа должна быть выполнена в срок в соответствии с учебным планом-графиком. В период сессии работа на проверку не будут приниматься. 10. Студент, не имеющий зачета по контрольной работе, к экзамену не допускается. 11. Во время экзамена зачтенная контрольная работа представляется преподавателю вместе с методическими рекомендациями. Контрольная работа имеет 10 вариантов. Варианты выбираются по последней цифре номера шифра зачетной книжки. Например, если последняя цифра номера шифра зачетной книжки равна 5, то студент должен решать примеры и задачи под номерами, которые оканчиваются на цифру 5, то есть 5, 15, 25, 35, 45, 55, 65, 75, 85, 95, 105, 115 если последняя цифра номера шифра зачетной книжки – 0, то номера примеров и задач – 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120 и т.д. Системы линейных уравнений Пользуясь формулами Крамера, решить систему линейных уравнений: 11. 3X1 – 5X2 + 3X3 = 46, X1 + 2X2 + X3 = 8, X1 – 7X2 – 2X3 = 5 12. X1 + 2X2 – X3 = – 3, 2X1 + 3X2 + X3 = – 1, X1 – X2 – X3 = 3 13. 2X1 – 3X2 + 5X3 = – 7, X1 + X2 + X3 = – 4, 5X1 + 3X2 – 4X3 = 11 14. 2X1 + 3X2 – 4X3 = – 4, 3X1 + 2X2 + 5X3 = 22, X1 – X2 + X3 = 2 15. X1 + 2X2 + X3 = 4, 3X1 - 5X2 + 3X3 = 1, 2X1 + 7X2 – X3 = 8 16. 2X1 - 4X2 + 9X3 = 28, 7X1 + 3X2 – 6X3 = – 1, 7X1 + 9X2 – 9X3 = 5 17. 7X1 + 2X2 + 3X3 = 15, 5X1 – 3X2 + 2X3 = 15, 10X1 – 11X2 + 5X3 = 36 18. 3X1 – 5X2 + 3X3 = 46, X1 + 2X2 + X3 = 8, X1 – 7X2 – 2X3 = 5 19. X1 – 4X2 – 2X3 = 0, 3X1 – 5X2 – 6X3 = – 21, 3X1 + X2 + 2X3 = – 4 20. 3X1 + X2 + 2X3 = 11, 2X1 + 2X2 – 3X3 = 9, X1 – 5X2 – 8X3 = 23 Пределы Найти пределы: 21. lim {[(X+3) 2 – 9] / 4X}; lim [(X 3 + 6 X 2 ) / (4X 3 – 7)] X® 0 X® ¥ 22. lim {[(X + 4) 2 – 16 ] / X 2}; lim [(X 4 + 6 X 2 ) / (4X 3 – 7)] 1. X® 0 X® ¥ 23. lim [( X® 9 X® ¥ 24. lim [(X 4 + 2X 2 + 1) / (3X4 – 2)]; lim [(X2 – 1) /(X2 – 3 X + 2)] X® ¥ X® 1 25. lim [( X® 16 X® ¥ 26. lim [(X 4 + X – 3) / (7X3 + 4X – 1)]; lim [(X – 8) / (X 2 – 9)] X® ¥ X® 5 27. lim [(3sin 4X) / 5X]; lim [(X2 + 9 X – 3) / (X3 + 4 X – 1)] X® 0 X® ¥ 28. lim [(tg 5X / sin 2X)]; lim [(X – 8) / (X – 9) ] X® 0 X® ¥ 29. lim [(2sin 3X) / X]; lim [(X3 + 9 X – 3) / (X2 + 4 X – 1)] X® 0 X® ¥ 30. lim [(sin X – sin 3X) / 7X]; lim [X / (X 2 + 9 X – 1)] X® 0 X® ¥ Производные. Экстремумы Найти производные: 31. а) f (X) = sin 2X + X2 + X + 32. a) f (X) = (X4 – X + 6) / 2X; б) f (X) = ln sin X – 4 cos2 X 33. a) f (X) = (X4 + 6) / 9X; б) f (X) = ln еX – 4 sin3 X 34. a) f (X) = 2X (X5 – 4X + 8) – tg X; б) f (X) = sin 3X – 4cos3 X 35. a) f (X) = X + tg X + 36. a) f (X) = (X4 + 4) / X; б) f (X) = X ln X – cos 3X 37. a) f (X) = X (X3 + 8) – ln X; б) f (X) = ln 3X – 4cos5X – 10 38. а) f (X) = cos X+ X + 39. а) f (X) = 10X + ctg X + 40. а) f (X) = sin 10X + tg X + Найти экстремумы функций: 41. Y = Х3 / 3 – 1,5Х2 – 4Х + 12 42. Y = Х3 – 12Х 43. Y = 2Х3 + 3Х2 – 12Х – 8 44. Y = 0,25Х4 + Х 45. Y = Х3 / 3 + 2Х2 + 3Х + 4 46. Y = 2Х3 – 9Х 2 + 12Х – 1 47. Y = Х3 – 6Х2 + 9Х 48. Y = 0,25Х4 – Х 49. Y = Х3 / 3 – Х2 – 3Х + 4; 50. Y = Х3 – 3Х + 1 Интегральное исчисление Найти интегралы: 51. а) ò 3(1 – 2 sin2X) / sin2X] dX; б) в) 52. а) ò [(2 – cos3X) / cos2X] dX; б) в) 53. а) ò [(Х3sin X – X + 5) / Х3)] dX; б) в) 54. а) ò [(2Х10 – 3Х5 сos X + 1) / Х5] dX; б) в) 55. а) ò [( в) 56. а) ò [(е2Х + еХ cos X) / еХ)] dX; б) в) 57. а) ò [(3 + 2сos2X) / сos2X)] dX; б) в) 58. а) ò [(3сos3X - 5) / сos2X)] dX; б) в) 59. а) ò [(Х2 sin X - в) 60. а) ò [(Хсos X - в) Сделать чертеж и вычислить площадь фигуры, ограниченной линиями: 61. Y = - Х2 + 8Х - 7 и осью OX; 62. Y = Х3 – 1, Y = 0, X = 2; 63. Y = Х2 - 3Х - 4 и осью OX; 64. Y2 = 4Х, Х2 = 4 Y; 65. Y = - Х2 + 5Х + 6 и осью OX; 66. Y = Х3, Y = Х2, Х = - 1, X = 0; 67. Y = Х2 - 6Х + 8 и осью OX; 68. Y = Х2, Y = Х + 2; 69. Y = Х2 - 4Х - 5 и осью OX; 70. Y = - 3Х2 + 6Х и осью OX. Решить дифференциальные уравнения и найти частное решение: 71. (X + 1)3 dY (Y - 2)2 dX = 0, Y = 0 при X = 0; 72. (X Y2 + X) dX + (Y X2 + Y) dY = 0, Y = 1 при X = 0; 73. (X Y2 + Y2) dX + (X2 - Y X2) dY = 0, Y = 1 при X = 1; 74. (1 + Y2) dX + Y X dY = 0, Y = 1 при X = 2; 75. (1 + X2) dY - 2Y X dX = 0, Y = 1 при X = 0; 76. (1 - X2)Y1 + Y X = 0, Y = 4 при X = 0; 77. Y1 = X / 78. X YY1 = 1 - X2, Y = 1 при X = 1; 79. (X Y + Y) dX + (X - Y X) dY = 0, Y = 1 при X = 1; 80. Решить однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: 81. Y11 – 5Y1 + 6Y = 0; 82. Y11 + 2Y1 + Y = 0; 83. 3Y11 - Y1 - Y = 0; 84. Y11 + 4Y1 + 3Y = 0; 85. Y11 – 2Y1 + Y = 0; 86. Y11 - Y = 0; 87. Y11 - 2Y = 0; 88. Y11 + 5Y1 + 4Y = 0; 89. Y11 – 8Y1 + 7Y = 0; 90. Y11 – 4Y1 + 4Y = 0 РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА а) основная литература: 1. Кремер Н., Путко Б. и др. Высшая математика для экономистов. – М.: Банки и биржи, 1997. 2. Турецкий В. Математика и информатика. – М.: ИНФРА-М, 2004. 3. Баврин И. Высшая математика. – М.: ACADEMA, 2003. 4. Данко П. и др. Высшая математика в упражнениях и задачах: Ч. 1,2. – М.: Высшая школа, любое издание. 5. Алгебра и начала анализа: Ч. 1, 2 / Под ред. Г. Яковлева, 1987. 6. Гмурман В. Теория вероятностей и математическая статистика. – М.: Высшая школа,1998. 7. Гмурман В. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа,1998. 8. Красс М. Математика для экономических специальностей. – М.: ИНФРА-М, 1999. б) дополнительная литература: 1. Шипачев В. Курс высшей математики. – М.: Высшая школа, 1993. 2. Шипачев В. Сборник задач по высшей математике. – М.: Высшая школа, 1993. 3. Бугров Я., Никольский С. Элементы линейной алгебры и аналитической геометрии. – Ростов н/Д, Феникс, 1997. 4. Богомолов Н. Практические занятия по математике. – М.: Высшая школа,1983. 5. Венцель Е. Теория вероятности. – М.: ACADEMA, 2003 6. Солодовников А., Бабайцев В. и др. Математика в экономике: Ч. 1, 2. – М.: Финансы и статистика, 1999.
Пояснительная записка Методические рекомендации по выполнению контрольной работы по математике реализуют государственные требования к содержанию и уровню подготовки выпускников обучающихся заочно по специальности «Социально-культурный сервиз и туризм» (230500) в условиях действия государственного образовательного стандарта высшего профессионального образования, оказание помощи студентам-заочникам в организации их самостоятельной работы над изучением учебного материала. 1. Цели дисциплины: § сформировать у студента навыки математического мышления, заключающиеся в умении применять математические методы для изучения закономерностей природы и общества. Полученные знания будут способствовать повышению общей культуры, выработке умений проводить математические исследования в образовательном учреждении, находить оптимальные пути достижения цели, преодоления профессиональных трудностей. 2. Задачи дисциплины: § изучение математики вооружает студентов основами математических знаний, умений и навыков в объеме, необходимом для повседневной практики, для усвоения экономических предметов, а также для дальнейшего повышения квалификации путем самообразования. 3. Место дисциплины в учебном плане Программа курса «Математика» разработана для студентов, чья компетентность и культура органичными составными частями войдут в структуру будущей профессиональной деятельности специалиста по сервисному обслуживанию и туризму. Математика
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.52.26 (0.01 с.) |


 = 15
= 15
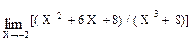
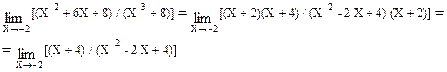
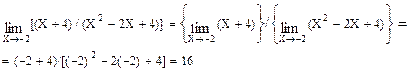

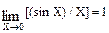
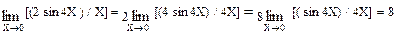
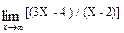
 ¥/¥. Разделим на Х числитель и знаменатель дроби, а затем, применив теоремы для пределов, получим
¥/¥. Разделим на Х числитель и знаменатель дроби, а затем, применив теоремы для пределов, получим
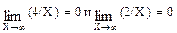 .
.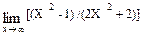 .
.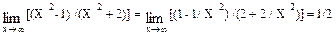
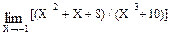
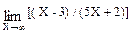
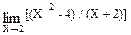
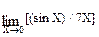
 dY / Y =
dY / Y =  ) < μ < XB + t (sx /
) < μ < XB + t (sx /  /
/  – 3) / (X – 9) ]; lim [(5X2 – 7X – 3) / (4X2 + 4X – 1)]
– 3) / (X – 9) ]; lim [(5X2 – 7X – 3) / (4X2 + 4X – 1)]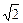 ; б) f (X) = еtgX – ln X 3
; б) f (X) = еtgX – ln X 3 ; б) f (X) = еtgX – ln X 3
; б) f (X) = еtgX – ln X 3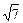 ; б) f (X) = еsin X – X3
; б) f (X) = еsin X – X3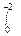 (1 – Х)2 dX;
(1 – Х)2 dX;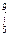 [X
[X  ] dX;
] dX;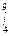 (2 – 1 /
(2 – 1 / 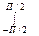 sin4X cos X dX;
sin4X cos X dX;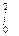 (1 + X - Х2) dX;
(1 + X - Х2) dX;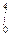 (X /
(X / 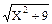 ) dX;
) dX;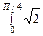 sin X dX;
sin X dX; 2Х3 (3Х4 + 1) dX;
2Х3 (3Х4 + 1) dX; (sin X / cos4X) dX;
(sin X / cos4X) dX;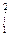 [X / (Х2 + 1)] dX;
[X / (Х2 + 1)] dX;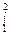 (2X - 3Х2 + 1) dX;
(2X - 3Х2 + 1) dX;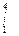 (1 /
(1 / 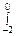 (X - Х2 + 1) dX;
(X - Х2 + 1) dX;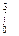 (7X - Х2/3 + 9) dX;
(7X - Х2/3 + 9) dX;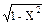 , Y = 1 при X = 0;
, Y = 1 при X = 0;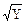 dX = 0, Y = 0 при X = 0.
dX = 0, Y = 0 при X = 0.


