
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы нахождения интеграловСодержание книги Поиск на нашем сайте
Пример 7. Найти неопределенный интеграл Решение: Данный интеграл будем находить методом подстановки (заменой переменной). 1. Введем новую переменную t = Х 2 + 1 2. Найдем дифференциал от подстановки (переменной): dt = 2XdX 3. В подынтегральном выражении переменную Х заменим на t:
4. Полученный интеграл – табличный, находим его и возвращаемся к старой переменной:
где С – константа интегрирования. Пример 8. Найти неопределенный интеграл Решение: Этот интеграл будем находить методом по частям. 1. Запишем формулу интегрирования по частям
2. Разобьем подынтегральное выражение на две части, причем, одну часть обозначаем U = X, а другую dV = SinХdX. 3. Найдем функцию V = 4. Подставим V и dU в формулу интегрирования по частям и находим интеграл:
Пример 9. Найти определенный интеграл Решение: Вычислим этот интеграл, используя таблицу простейших интегралов и основные свойства определенного интеграла.
Применение определенного интеграла для определения площадей плоских фигур Пример 10. Вычислить площадь плоской фигуры, ограниченной линиями Y = Х 2 и Y = Х. Решение: 1. Построим графики этих функций, которые ограничивают площадь плоской фигуры (см. Рис.3).
Рис.3. Нахождение площади плоской фигуры, ограниченной двумя линиями. 2. Определим пределы интегрирования. Для этого найдем точки пересечения этих линий, решая систему уравнений:
Получим уравнение Х2 = Х. Решив это уравнение, находим корни: X1 = 0 и X2 = 1. Это есть точки пересечения графиков и пределы интегрирования. 3. Запишем формулу для нахождения площади нашей фигуры и вычислим ее: S = S (площадь прямоугольного треугольника) – S (площадь криволинейного треугольника) (см. Рис. 3) S = Ответ: S = 1 / 6 кв. ед. Вопросы и упражнения для самоконтроля: 1. Какое действие называется интегрированием? 2. Какая функция называется первообразной для функции f(X)? 3. Дайте определение неопределенного интеграла. 4. Перечислите основные свойства неопределенного интеграла. 5. Каким действием можно проверить интегрирование? 6. Напишите основные формулы интегрирования (табличные интегралы). 7. Дайте определение неопределенного интеграла. 8. В чем заключается геометрический смысл определенного интеграла? 9. Найдите интегралы: а) в) д) 10. Сделать чертеж и вычислить площадь фигуры, ограниченной линиями а) Y = (Х + 3) (Х – 2)и осьюOX; б) Y = Х3, Y = X. Дифференциальные уравнения Пример 11. Решить дифференциальное уравнение первого порядка dY / (Х 3 – 6) - Y dX = 0, Y = 1 при X = 0 Решение: 1. Это дифференциальное уравнение с разделяющимися переменными. Разделим переменные. Для этого, используя алгебраические преобразования, соберем в одной части уравнения X, dX, а в другой – Y, dY. dY / Y = (Х 3 – 6) dX 2. Интегрируем левую и правую части, полученного уравнения.
3. Результат интегрирования дает общее решение дифференциального уравнения. ln Y = Х 4 / 4 – 6X + C, где С – константа интегрирования. 4. Найдем частное решение. Для этого в общее решение подставим начальные условия (Y = 1 при X = 0) и найдем константу интегрирования С. Константа интегрирования С = 0. Частное решение запишется в виде ln Y = Х4 / 4 – 6X или Y = exp (Х4 / 4 – 6X) Ответ: Y = exp (Х4 / 4 – 6X). Пример 12. Решить однородное дифференциальное уравнение второго порядка с постоянными коэффициентами Y11 - 6 Y1 + 9Y = 0 Решение: Составляем характеристическое уравнение. k2 - 6 k + 9 = 0 Решая это квадратное уравнение, находим k1 = k2 = 3 (корни равные). 1. Если корни равные, то общее решение запишется Y = (C1 + C2 X) e3X Вопросы и упражнения для самоконтроля: 1. Какие уравнения называются дифференциальными? 2. Дайте определение дифференциального уравнения первого порядка. 3. Дайте определение общего решения дифференциального уравнения первого порядка. 4. Дайте определение частного решения дифференциального уравнения первого порядка. 5. Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. 6. Решить дифференциальные уравнения и найти частное решение (X + 1)2 dY - (Y - 2)3 dX = 0, Y = 0 при X = 0; (X Y + X) dX + (Y X + Y) dY = 0, Y = 1 при X = 0. 7. Решить однородные дифференциальные уравнения второго порядка с постоянными коэффициентами а) Y11 - 2 Y1 + 4Y = 0; б) Y11 - 2Y1 = 0
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.77.119 (0.006 с.) |

 .
.

 .
. 
 и дифференциал dU = dX.
и дифференциал dU = dX.
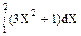 .
.



 [(1 – sin2X) / sin2X] dX; б)
[(1 – sin2X) / sin2X] dX; б) 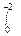 (1 – Х)3 dX;
(1 – Х)3 dX; ) / Х] dX; г)
) / Х] dX; г)  [еХ / (еХ + 1) ] dX;
[еХ / (еХ + 1) ] dX; dY / Y =
dY / Y = 


