Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов прямых многократных измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Последовательность обработки результатов прямых многократных измерений состоит из ряда этапов.
1. Определение точечных оценок закона распределения результатов измерений На этом этапе определяются среднее арифметическое значение В соответствии с критериями, грубые погрешности исключаются, после чего проводится повторный расчет оценок среднего арифметического значения и его СКО. 2. Определение закона распределения результатов измерений или случайных погрешностей Здесь по результатам измерений и проведенным расчетам строится гистограмма или полигон. По виду построенных зависимостей может быть оценен закон распределения результатов измерений.
3. Оценка закона распределения по статистическим критериям При числе измерений n > 50 для идентификации закона распределения используется критерий Пирсона. При 50 > n >15 для проверки нормальности закона распределения применяется составной критерий. При n < 15 принадлежность экспериментального распределения к нормальному не проверяется.
4. Определение доверительных границ случайной погрешности Если удалось идентифицировать закон распределения результатов измерений, то с его использованием находят квантильный множитель zp при заданном значении доверительной вероятности Р. В этом случае доверительные границы случайной погрешности Здесь tP – коэффициент Стьюдента, приведенный в табл. 23, n – количество измерений.
Таблица № 23 Величина tP при различных уровнях значимости
5.Определение границ неисключенной систематической погрешности результата измерения Под этими границами понимают найденные нестатистическими методами границы интервала, внутри которого находится неисключенная систематическая погрешность. Границы неисключеной систематической погрешности принимаются равными пределам допускаемых основных и дополнительных погрешностей средств измерений, если их случайные составляющие пренебрежимо малы.
6. Определение доверительных границ погрешности результата измерения
Данная операция осуществляется путем суммирования СКО случайной составляющей
7. Запись результата измерения
Результат измерения записывается в виде
Пример Произвести обработку результатов измерений, данные которых представлены в табл. 24.
Таблица № 24 Результаты измерений
1.Определение точечных оценок закона распределения результатов измерений
Определяем среднее арифметическое значение результатов измерений
Среднее квадратическое отклонение результатов измерения
Производим проверку на наличие грубых погрешностей в результатах измерения по критерию Диксона. Составим вариационный возрастающий ряд из результатов измерений: 36,007; 36,008; 36,009; 36,010; 36,011; 36,012. Найдем расчетное значение критерия для значения 36,012
Как следует из таблицы 5, по этому критерию результат 36,012 не является промахом при всех уровнях значимости.
2. Предварительная оценка вида распределения результатов измерений или случайных погрешностей При числе измерений меньше 15 предварительная оценка вида распределения результатов наблюдений не производится
3.Оценка закона распределения по статистическим критериям При n < 15 принадлежность экспериментального распределения к нормальному не проверяется.
4.Определение доверительных границ случайной погрешности При числе измерений n= 11 используем распределение Стьюдента, при этом доверительные границы случайной погрешности Коэффициент Стьюдента при доверительной вероятности Рд = 0,95 и при n = 11 равен 2,23. Тогда доверительные границы случайной погрешности
5.Определение границ неисключенной систематической погрешности результата измерения Границы неисключенной систематической погрешности q принимаются равными пределам допускаемых основных и дополнительных погрешностей средства измерения. Для рычажного микрометра допускаемая погрешность равна ± 0,7 мкм.
6. Определение доверительных границ погрешности результата измерения
Согласно ГОСТ 8.207–76 погрешность результата измерения определяется по следующему правилу. Если границы неисключенной систематической погрешности q < 0,8 Sx, то следует пренебречь систематической составляющей погрешности и учитывать только случайную погрешность результата. В нашем случае q = 1,4 мкм, а Sx = 2 мкм, т.е. соотношение q < 0.8 Sx выполняется, поэтому систематической погрешностью пренебрегаем.
7. Запись результата измерения
Результат измерения –
Задание Используя данные в таблице №25 произвести обработку результатов прямых многократных измерений
Таблица № 25
Практическое занятие №5
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 1104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.153.240 (0.006 с.) |

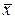 измеряемой величины, СКО результата измерений Sx.
измеряемой величины, СКО результата измерений Sx.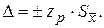 Здесь
Здесь  – СКО среднего арифметического значения. При n < 30 часто используют распределение Стьюдента, при этом доверительные границы случайной погрешности
– СКО среднего арифметического значения. При n < 30 часто используют распределение Стьюдента, при этом доверительные границы случайной погрешности 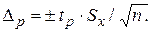
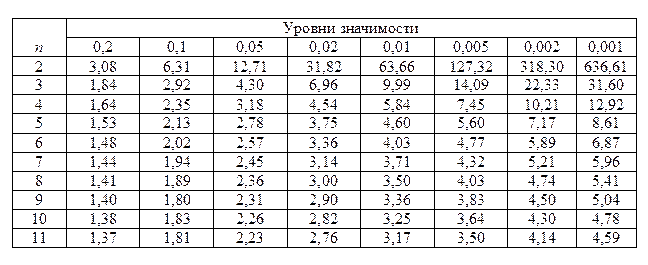
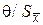 .
.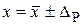 при доверительной вероятности Р = Рд.
при доверительной вероятности Р = Рд.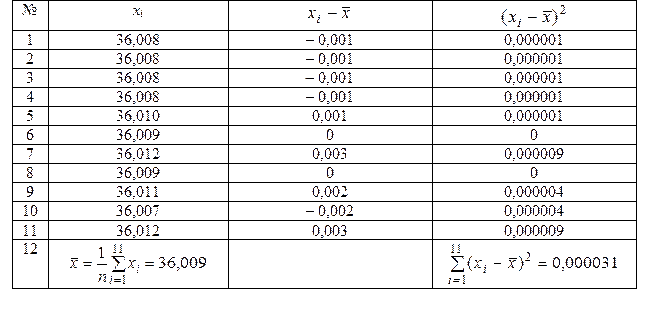
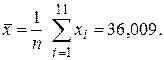
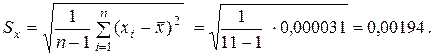
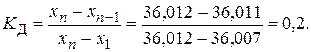
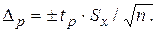
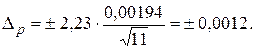
 при доверительной вероятности Р = 0,95.
при доверительной вероятности Р = 0,95.