Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классы точности средств измеренийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В большинстве производственных отраслей, в том числе в строительстве, используют рабочие средства измерений, метрологические характеристики которых нормированы на основе классов точности. Класс точности – обобщенная характеристика средств измерений определенного типа, позволяющая судить о том, в каком диапазоне находится суммарная погрешность измерений. Общие требования при делении средств измерений на классы точности приведены в ГОСТ 8.401 – 80 «Классы точности средств измерений. Общие требования.» Обозначение классов точности наносятся на циферблаты, щитки и корпуса средств измерений. Обозначения могут иметь форму заглавных букв латинского алфавита и римских цифр с добавлением условных знаков. Если же класс точности обозначается арабскими цифрами с добавлением какого-либо знака, то эти цифры непосредственно оценивают погрешность измерения. 1. Пределы допускаемой абсолютной основной погрешности устанавливают по формуле или где Δ - пределы допускаемой абсолютной основной погрешности, выраженной в единицах измеряемой величины на входе (выходе) или условно в делениях шкалы; х - значение измеряемой величины на входе (выходе) средств измерений или число делений, отсчитанных по шкале; a, b - положительные числа, не зависящие от х. В обоснованных случаях пределы допускаемой абсолютной погрешности устанавливают по более сложной формуле или в виде графика либо таблицы.
2. Пределы допускаемой приведенной основной погрешности следует устанавливать по формуле где γ - пределы допускаемой приведенной основной погрешности, %; Δ - пределы допускаемой абсолютной основной погрешности, устанавливаемые по формуле (1); X N - нормирующее значение, выраженное в тех же единицах, что и Δ; р - отвлеченное положительное число, выбираемое из ряда 1·10 n ; 1,5·10 n ; (1,6·10 n ); 2·10 n ; 2,5·10 n ; (3·10 n ); 4·10 n ; 5·10 n ; 6·10 n ; (n =1, 0, -1, -2, и т. д.). Значения, указанные в скобках, не устанавливают для вновь разрабатываемых средств измерений. При одном и том же показателе степени n допускается устанавливать не более пяти различных пределов допускаемой основной погрешности для средств измерений конкретного вида.
3. Пределы допускаемой относительной основной погрешности устанавливают по формуле
если Δ установлено по формуле (1), или по формуле где δ - пределы допускаемой относительной основной погрешности, %; Δ, x - см. п. 1; q - отвлеченное положительное число, выбираемое из ряда, приведенного в п. 2; Х K - больший (по модулю) из пределов измерений; с, d - положительные числа, выбираемые из ряда, приведенного в п. 2. a, b - см. п. 1. Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице. Таблица
Пример Определить в каком интервале находится измеренное значение, если при выполнении измерения прибором, имеющим на щитке обозначение
Решение Определяем абсолютную погрешность измерения И измеряемое значение будет находиться в интервале 200±1 Задание
Практическое занятие №7 ВЫБОР СРЕДСТВ ИЗМЕРЕНИЙ.
Расчет погрешности при выборе методов и средств измерения выполняют в соответствии с требованиями ГОСТ 26433.0-85. Методы и средства измерений принимаем в соответствии с характером объекта и измеряемых параметров из условия. где
Вычисляем расчетную погрешность измерения по одной из формул: или где
При расчете по указанным формулам принимаем, что составляющие погрешности независимы между собой или слабо коррелированны.
Предельную погрешность где К - коэффициент, зависящий от цели измерений и характера объекта. Для измерений, выполняемых в процессе и при контроле точности изготовления и установки элементов, а также при контроле точности разбивочных работ принимаем К = 0,2. Для измерений, выполняемых в процессе производства разбивочных работ, К = 0,4. Действительная погрешность Для случаев, когда процесс измерения состоит из большого числа отдельных операций, на основе принципа равных влияний определяем среднее значение составляющих погрешностей где Выделяем те составляющие погрешности, которые легко могут быть уменьшены, увеличивая соответственно значения тех составляющих погрешностей, которые трудно обеспечить имеющимися методами и средствами. Проверяем соблюдение условия (1) и в случае несоблюдения этого условия назначают более точные средства или принимают другой метод измерения.
Пример Выбрать средство измерения для контроля длины изделия, L = 3600 ± 2,0 мм (
Решение 1. Определяем предельную погрешность измерения 2. Для выполнения измерений применяем, например, 10-метровую металлическую рулетку 3-го класса точности ЗПК3-10АУТ/10 ГОСТ 7502-80. 3. В суммарную погрешность измерения длины изделия рулеткой входят составляющие погрешности: Определяем значения этих погрешностей. 3.1. Погрешность 3.2. Погрешность 3.3. Погрешность
где F = 2 мм2 - площадь поперечного сечения рулетки; E = 2·105Н/мм - модуль упругости материала рулетки. 3.4. Экспериментально установлено, что погрешность снятия отсчета по шкале рулетки не превышает 0,3 мм, при этом погрешность 4. Определяем расчетную суммарную погрешность измерения по формуле (2), учитывая, что 5. Данные метод и средство измерения могут быть приняты для выполнения измерений, так как расчетная суммарная погрешность измерения
Задание
По выше описанному алгоритму произвести выбор средства измерения с учетом погрешности, используя данные в таблице №6
Таблица № 6
Практическое занятие №8
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 727; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.222.102 (0.008 с.) |

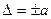 (1)
(1)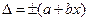 , (2)
, (2)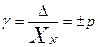 , (3)
, (3)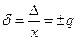 , (4)
, (4)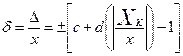 , (5)
, (5)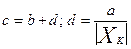 ;
;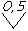
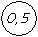
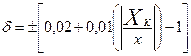
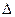
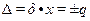
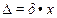 = 0,005·200 = ±1
= 0,005·200 = ±1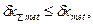 (1)
(1)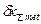 - расчетная суммарная погрешность принимаемого метода и средства измерения;
- расчетная суммарная погрешность принимаемого метода и средства измерения;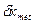 - предельная погрешность измерения.
- предельная погрешность измерения.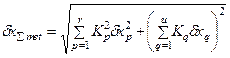 (2)
(2)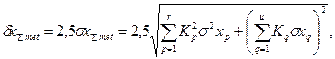 (3)
(3)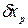 - случайные составляющие погрешности;
- случайные составляющие погрешности;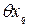 - систематические составляющие погрешности;
- систематические составляющие погрешности;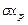 - средние квадратические случайные составляющие погрешности;
- средние квадратические случайные составляющие погрешности;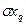 - средние квадратические систематические составляющие погрешности;
- средние квадратические систематические составляющие погрешности;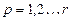 - число случайных составляющих погрешностей;
- число случайных составляющих погрешностей;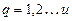 - число систематических составляющих погрешностей;
- число систематических составляющих погрешностей;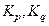 - коэффициенты, учитывающие характер зависимости между суммарной и каждой из составляющих погрешностей измерения.
- коэффициенты, учитывающие характер зависимости между суммарной и каждой из составляющих погрешностей измерения.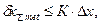 (4)
(4)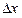 - допуск измеряемого геометрического параметра, установленный нормативно-технической документацией на объект измерения;
- допуск измеряемого геометрического параметра, установленный нормативно-технической документацией на объект измерения;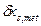 выполненных измерений не должна превышать ее предельного значения.
выполненных измерений не должна превышать ее предельного значения.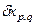 по формуле
по формуле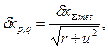 (5)
(5)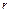 - число случайных составляющих погрешностей;
- число случайных составляющих погрешностей;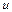 - число систематических составляющих погрешностей.
- число систематических составляющих погрешностей.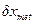
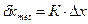 мм
мм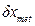 = 0,2·4,0 = 0,8 мм
= 0,2·4,0 = 0,8 мм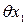 - поверки рулетки;
- поверки рулетки; 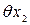 - от погрешности измерения температуры окружающей среды;
- от погрешности измерения температуры окружающей среды; 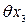 - от колебания силы натяжения рулетки;
- от колебания силы натяжения рулетки; 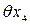 - снятия отсчетов по шкале рулетки на левом и правом краях изделия.
- снятия отсчетов по шкале рулетки на левом и правом краях изделия.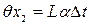 мм.
мм.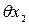 = 3600·12,5·10-6·0,5» 0,22 мм.
= 3600·12,5·10-6·0,5» 0,22 мм.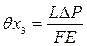 мм,
мм,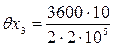 = 0,09» 0,1 мм,
= 0,09» 0,1 мм,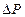 = 10Н - погрешность натяжения рулетки вручную;
= 10Н - погрешность натяжения рулетки вручную;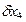 снятия отсчетов на левом и правом краях изделия составит
снятия отсчетов на левом и правом краях изделия составит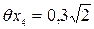 мм.
мм.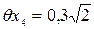 »0,4 мм.
»0,4 мм.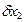 ,
, 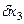 и
и 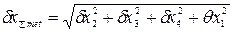 мм.
мм.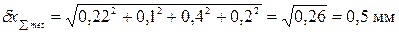
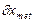 = 0,8 мм, что соответствует требованию.
= 0,8 мм, что соответствует требованию.